1. Aprendizaje supervisado

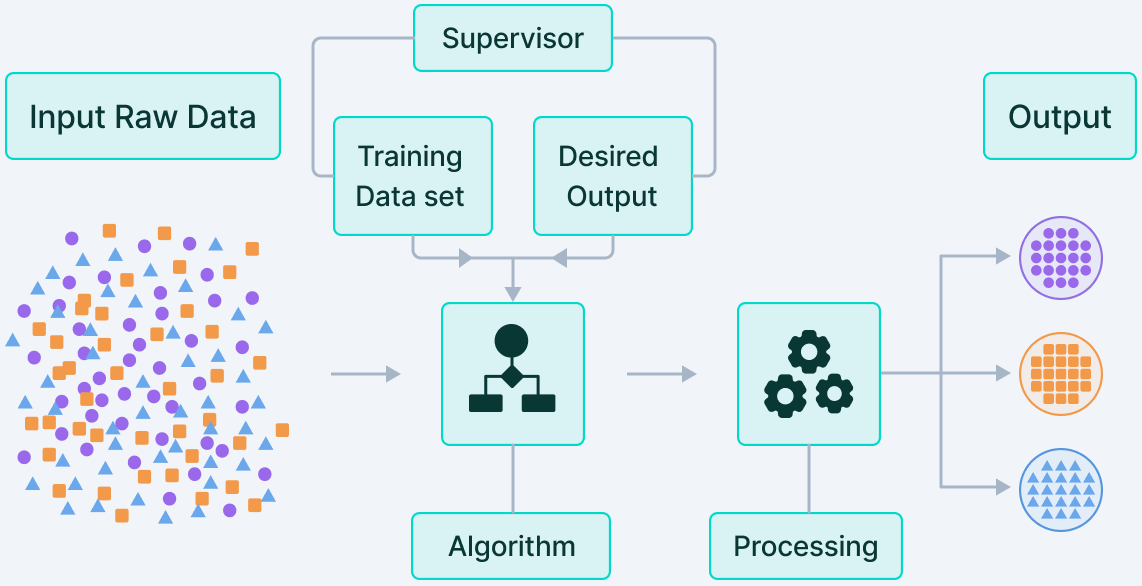
Fig. 1.1 Aprendizaje Supervisado. Source: v7labs.com.

Introducción

• Los algoritmos de aprendizaje automático más eficaces automatizan la toma de decisiones mediante la generalización a partir de ejemplos. El aprendizaje supervisado es un ejemplo claro, donde se proporcionan pares de entradas y salidas deseadas (datos etiquetados) para entrenar modelos que clasifiquen datos o predigan resultados con precisión.

• El algoritmo ajusta sus ponderaciones mediante validación cruzada hasta que se adapta correctamente. Así, puede producir resultados precisos para nuevas entradas sin intervención humana, gracias a la supervisión inicial que recibe.

1.1. Ejemplos de tareas de aprendizaje automático supervisado

• Identificar el código postal a partir de los dígitos escritos a mano en un sobre: Aquí la entrada es un escaneo de la escritura a mano, y la salida deseada son los dígitos reales del código postal. Para crear un conjunto de datos con el fin de construir un modelo de aprendizaje automático, hay que recoger muchos sobres. Entonces puedes leer los códigos postales tú mismo y almacenar los dígitos como los resultados deseados.

• Determinar si un tumor es benigno a partir de una imagen médica: Aquí la entrada es la imagen, y la salida es si el tumor es benigno. Para crear un conjunto de datos para construir un modelo, se necesita una base de datos de imágenes médicas. También se necesita la opinión de un experto, por lo que un médico tiene que ver todas las imágenes y decidir qué tumores son benignos y cuáles no. Incluso puede ser necesario hacer un diagnóstico adicional más allá del contenido de la imagen para determinar si el tumor de la imagen es cancerígeno o no.

• Detección de actividades fraudulentas en transacciones con tarjetas de crédito Aquí la entrada es un registro de la transacción de la tarjeta de crédito, y la salida es si es probable que sea fraudulenta o no. Suponiendo que usted es la entidad que distribuye las tarjetas de crédito, recopilar un conjunto de datos significa almacenar todas las transacciones y registrar si un usuario denuncia alguna transacción como fraudulenta.

1.2. Clasificación y regresión

• Hay dos tipos principales de problemas de aprendizaje automático supervisado, denominados clasificación y regresión. En la clasificación, el objetivo es predecir una etiqueta de clase, que es una elección entre una lista predefinida de posibilidades. La clasificación se divide en clasificación binaria, que es el caso especial de distinguir entre exactamente dos clases, y clasificación multiclase, que es la clasificación entre más de dos clases. Se puede pensar en la clasificación binaria como si se tratara de responder sí/no a una pregunta. Clasificar los correos electrónicos como spam o no spam es un ejemplo de problema de clasificación binaria.

• En la clasificación binaria se suele hablar de que una clase es la positiva y la otra la negativa. Aquí, positivo no representa tener un beneficio o un valor, sino cuál es el objeto de estudio. Así, cuando se busca el spam, “positivo” podría significar la clase de spam. Cuál de las dos clases se denomina positiva suele ser una cuestión subjetiva y específica del ámbito.

• En las tareas de regresión, el objetivo es predecir un número continuo, o flotante en términos de programación (o un número real en términos matemáticos). Predecir los ingresos anuales de una persona a partir de su educación, su edad y su lugar de residencia es un ejemplo de tarea de regresión. Al predecir los ingresos, el valor predicho es una cantidad, y puede ser cualquier número en un rango determinado.

• Una forma fácil de distinguir entre las tareas de clasificación y las de regresión es preguntarse si hay algún tipo de continuidad en el resultado. Si hay continuidad entre los posibles resultados, el problema es de regresión. En cambio, para la tarea de reconocer el idioma de un sitio web (que es un problema de clasificación), no hay cuestión de grado. Un sitio web está en un idioma o en otro. No hay continuidad entre las lenguas, y no hay ninguna lengua que esté entre el inglés y el francés.

1.3. Generalización, sobreajuste y subajuste

• En el aprendizaje supervisado, queremos construir un modelo sobre los datos de entrenamiento y luego ser capaces de realizar predicciones precisas, sobre datos desconocidos que tengan las mismas características que el conjunto de entrenamiento que hemos utilizado. Si un modelo es capaz de realizar predicciones precisas, sobre datos desconocidos, decimos que es capaz de generalizar del conjunto de entrenamiento al conjunto de prueba. Queremos construir un modelo que sea capaz de generalizar con la mayor precisión posible.

• Por lo general, construimos un modelo de manera que pueda hacer predicciones precisas en el conjunto de entrenamiento. Si los conjuntos de entrenamiento y de prueba tienen suficientes puntos en común, esperamos que el modelo también sea preciso en el conjunto de prueba. Sin embargo, hay algunos casos en los que esto puede no funcionar. Por ejemplo, si nos permitimos construir modelos muy complejos, podemos siempre ser tan precisos como queramos en el conjunto de entrenamiento, pero que no es capaz de generalizarse a nuevos datos (sobreajuste).

• El sobreajuste (overfitting) se produce cuando se ajusta un modelo demasiado a las particularidades del conjunto de entrenamiento, y se obtiene un modelo que funciona bien en el conjunto de entrenamiento pero no es capaz de generalizarse con nuevos datos. Por otro lado, si el modelo es demasiado simple, es posible que no sea capaz de captar todos los aspectos y la variabilidad de los datos, y el modelo funcionará mal incluso en el conjunto de entrenamiento. La elección de demasiado simple se denomina subajuste (underfitting)

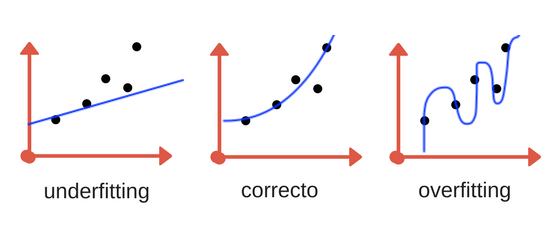
Fig. 1.2 Overfitting y Underfitting. Fuente aprendemachinelearning.

Observación

• Cuanto más complejo permitimos que sea nuestro modelo, mejor podremos predecir en los datos de entrenamiento. Sin embargo, si nuestro modelo se vuelve demasiado complejo, empezamos a centrarnos demasiado en cada punto de datos individual de nuestro conjunto de entrenamiento, y el modelo no se generalizará correctamente con nuevos datos.

• Hay un punto intermedio (sweet spot) en el que se obtiene el mejor rendimiento de generalización. Este es el modelo que queremos encontrar. El equilibrio entre overfitting y underfitting.

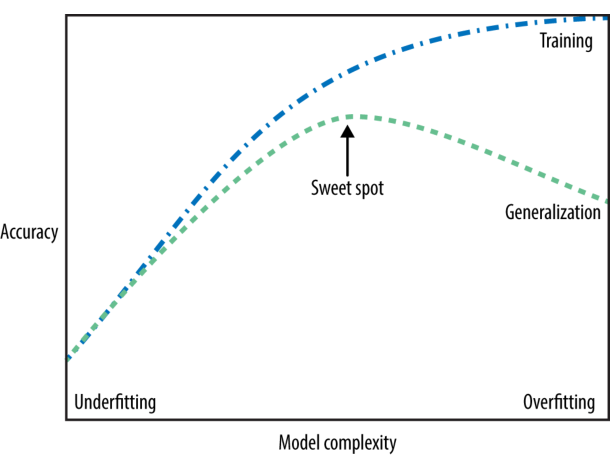
Fig. 1.3 Complejidad vs precisión para entrenamiento y prueba. Source: towardsai.net.

¿Qué diferencia es aceptable?

• No hay una regla fija, para decidir si es aceptable la diferencia entre el desempeño en el conjunto de entrenamiento (train) y el de prueba (test), pero generalmente:

  • Diferencias menores al 5-10% en el score suelen ser aceptables.

  • Diferencias mayores al 15-20% indican que el modelo podría estar sobreajustado y necesita ajustes (regularización, más datos, reducción de complejidad, etc.).

• Conclusión: Si nota que el modelo rinde excepcionalmente bien en entrenamiento, pero mal en prueba, es probable que esté memorizando en lugar de aprender patrones generales. Evaluar la diferencia entre los scores en train y test es clave para detectar y corregir el sobreajuste.

1.4. Enfoque estadístico para detectar sobreajuste

• El sobreajuste se puede verificar formulando una prueba de hipótesis donde:

  • \(H_0:~\textsf{No hay diferencia significativa en el rendimiento entre el conjunto de entrenamiento y prueba.}\)

  • \(H_1:~\textsf{Existe una diferencia significativa en el rendimiento entre ambos conjuntos, lo que sugiere sobreajuste.}\)

Métodos para probarlo

• Prueba \(t\) para muestras pareadas

  • Si tienes múltiples folds en validación cruzada, puedes comparar los scores del modelo en entrenamiento y prueba con una prueba t de muestras pareadas:

  • Si el \(p\)-valor es menor a 0.05, hay evidencia estadística de que el modelo tiene una diferencia significativa de rendimiento, sugiriendo sobreajuste.

• Prueba de Wilcoxon (para datos no normales)

  • Si los scores no siguen una distribución normal, la prueba de Wilcoxon es una alternativa no paramétrica a la prueba \(t\).

• Intervalos de confianza para la diferencia de rendimiento

  • Puedes construir intervalos de confianza (por ejemplo, al 95%) para la diferencia entre los scores de entrenamiento y prueba.

  • Si el intervalo no incluye el cero, indica que la diferencia es significativa.

• Conclusión: Si la prueba de hipótesis muestra una diferencia estadísticamente significativa entre el desempeño en train y test, es una señal clara de sobreajuste. Sin embargo, también debes analizar la magnitud de la diferencia y considerar técnicas de regularización o aumento de datos para mejorar la generalización del modelo.

• Observe las siguientes simulaciones de lo mencionado anteriormente, usando Python

import numpy as np
from scipy import stats

train_scores = np.array([0.90, 0.92, 0.91, 0.93, 0.92])
test_scores = np.array([0.80, 0.82, 0.81, 0.79, 0.83])

t_stat, p_value_t = stats.ttest_rel(train_scores, test_scores)
w_stat, p_value_w = stats.wilcoxon(train_scores, test_scores)

diff = train_scores - test_scores
mean_diff = np.mean(diff)
conf_int = stats.t.interval(0.95, len(diff)-1, loc=mean_diff, scale=stats.sem(diff))

print(f"Prueba t: t-statistic = {t_stat:.3f}, p-valor = {p_value_t:.3f}")
print(f"Prueba de Wilcoxon: W-statistic = {w_stat:.3f}, p-valor = {p_value_w:.3f}")
print(f"Intervalo de confianza 95% para la diferencia: {conf_int}")

alpha = 0.05
if p_value_t < alpha:
    print("Existe una diferencia significativa entre Train y Test. Puede haber sobreajuste.")
else:
    print("No se encontró una diferencia significativa entre Train y Test.")

Prueba t: t-statistic = 12.159, p-valor = 0.000
Prueba de Wilcoxon: W-statistic = 0.000, p-valor = 0.062
Intervalo de confianza 95% para la diferencia: (0.08179551272830933, 0.13020448727169073)
Existe una diferencia significativa entre Train y Test. Puede haber sobreajuste.

train_scores = np.array([0.90, 0.92, 0.91, 0.93, 0.92])
test_scores = np.array([0.93, 0.90, 0.93, 0.90, 0.90])

t_stat, p_value_t = stats.ttest_rel(train_scores, test_scores)

w_stat, p_value_w = stats.wilcoxon(train_scores, test_scores)

diff = train_scores - test_scores
mean_diff = np.mean(diff)
conf_int = stats.t.interval(0.95, len(diff)-1, loc=mean_diff, scale=stats.sem(diff))

print(f"Prueba t: t-statistic = {t_stat:.3f}, p-valor = {p_value_t:.3f}")
print(f"Prueba de Wilcoxon: W-statistic = {w_stat:.3f}, p-valor = {p_value_w:.3f}")
print(f"Intervalo de confianza 95% para la diferencia: {conf_int}")

alpha = 0.05
if p_value_t < alpha:
    print("Existe una diferencia significativa entre Train y Test. Puede haber sobreajuste.")
else:
    print("No se encontró una diferencia significativa entre Train y Test.")

Prueba t: t-statistic = 0.331, p-valor = 0.757
Prueba de Wilcoxon: W-statistic = 6.500, p-valor = 1.000
Intervalo de confianza 95% para la diferencia: (-0.029547913849266645, 0.03754791384926665)
No se encontró una diferencia significativa entre Train y Test.

1.5. Relación entre la complejidad del modelo y el tamaño del conjunto de datos

• Es importante señalar que la complejidad del modelo está íntimamente ligada a la variación de entradas contenidas en el conjunto de datos de entrenamiento: cuanto mayor sea la variedad de puntos de datos, más complejo será el modelo que se puede utilizar sin sobreajustar. Por lo general, al recolectar más puntos de datos se obtiene un modelo más complejo sin que haya un exceso de ajuste. Sin embargo, la simple duplicación de los mismos puntos de datos o la recopilación de datos muy similares no ayudará.

• Disponer de más datos y construir modelos adecuadamente más complejos a menudo puede hacer maravillas en las tareas de aprendizaje supervisado. En este curso, nos centraremos en trabajar con conjuntos de datos de tamaño fijo. En el mundo real, a menudo se puede decidir la cantidad de datos que se van a recoger, lo cual puede ser más beneficioso que ajustar y afinar su modelo. Nunca subestime el poder de tener más datos.

1.6. Algoritmos de aprendizaje automático supervisado

• A continuación se abordarán los algoritmos de aprendizaje automático más populares. Se estudiará cómo aprenden de los datos y cómo hacen predicciones. También discutiremos el concepto de complejidad para cada uno de estos modelos, y proporcionaremos una visión general de cómo cada algoritmo construye un modelo. Examinaremos los puntos fuertes y débiles de cada algoritmo y a qué tipo de datos pueden aplicarse mejor. También explicaremos el significado de los parámetros y opciones más importantes. Muchos algoritmos tienen una variante de clasificación y otra de regresión, y describiremos ambas.

1.7. Algunos ejemplos de conjuntos de datos

• Utilizaremos varios conjuntos de datos para ilustrar los diferentes algoritmos. Algunos de los conjuntos de datos serán pequeños y sintéticos, diseñados para destacar aspectos concretos de los algoritmos. Otros conjuntos de datos serán ejemplos grandes del mundo real. Un ejemplo de conjunto de datos sintético de clasificación de dos clases es el conjunto de datos de forge, que tiene dos características.

• El siguiente código crea un gráfico de dispersión que visualiza todos los puntos de datos de este dataset. El gráfico tiene la primera característica en el eje \(x\) y la segunda en el eje \(y\). Como siempre ocurre en los gráficos de dispersión, cada punto de datos está representado por un punto. El color y la forma del punto indican su clase. Generamos el conjunto de datos usando la librería mglearn (también puede utilizar make_blobs de sklearn) e importamos warning para evitar mensajes molestos, relacionados con advertencias inofensivas o funciones obsoletas en la actual versión de Python. En el presente curso usaremos las versión 3.9 de Python.

• Para instalar mglearn en su ambiente para Machine Learning utilizar la siguiente orden

  pip install mglearn
  

• Si su algoritmo presenta algún problema a la hora de reconocer mglearn, para solucionar este problema, elimine su actual enviroment. Luego cree un nuevo enviroment y en este instale el requirement asociado a este curso. El archivo aparece en (ver requirements.txt).

  pip install -r requirements.txt
  

• Procedemos ahora sí a importar cada una de las librerías del ejemplo, incluyendo: matplotlib y numpy

import warnings
warnings.filterwarnings("ignore")

import mglearn
import matplotlib.pyplot as plt
import numpy as np

X, y = mglearn.datasets.make_forge()

• Trazamos el conjunto de datos

mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.legend(["Class 0", "Class 1"], loc=4)
plt.xlabel("First feature")
plt.ylabel("Second feature")
print("X.shape: {}".format(X.shape))

X.shape: (26, 2)

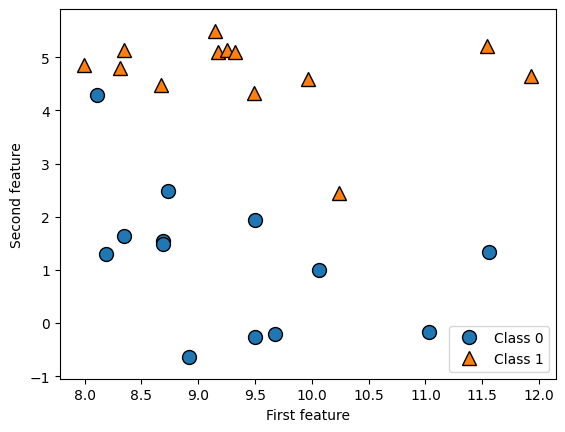
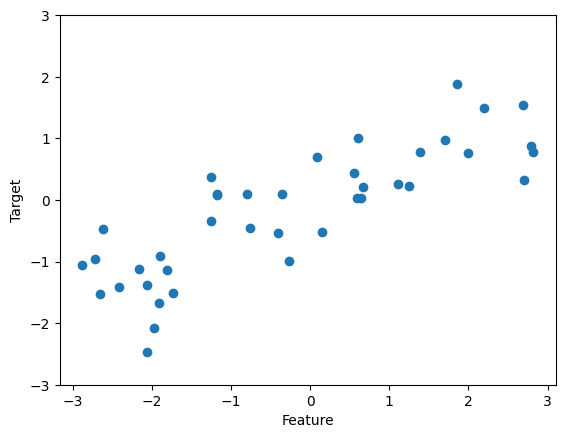
• Como se puede ver en X.shape, este dataset consta de 26 puntos de datos, con 2 características. Para ilustrar los algoritmos de regresión, utilizaremos el dataset sintético wave. Este dataset tiene una única característica de entrada y una variable objetivo continua (o respuesta) que queremos modelar.

X, y = mglearn.datasets.make_wave(n_samples=40)
plt.plot(X, y, 'o')
plt.ylim(-3, 3)
plt.xlabel("Feature")
plt.ylabel("Target");

• Complementaremos estos pequeños datasets sintéticos con dos conjuntos de datos del mundo real que se incluyen en scikit-learn. Uno de ellos es el conjunto de datos de cáncer de mama de Wisconsin (cancer, para abreviar), que registra mediciones clínicas de tumores de cáncer de mama. Cada tumor se etiqueta como benign (para tumores inofensivos) o malignant (para tumores cancerosos). La tarea es aprender a predecir si un tumor es maligno basándose en las mediciones del tejido. Los datos pueden cargarse con la función load_breast_cancer de scikit-learn

from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
print("cancer.keys(): \n{}".format(cancer.keys()))

cancer.keys(): 
dict_keys(['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names', 'filename', 'data_module'])

• Los conjuntos de datos que se incluyen en scikit-learn suelen almacenarse como objetos Bunch, que contienen alguna información sobre el conjunto de datos así como los datos reales. Todo lo que necesita saber sobre los objetos Bunch es que se comportan como diccionarios, con la ventaja añadida de que se puede acceder a los valores utilizando un punto (como en bunch.key en lugar de bunch['clave'] ).

print("Shape of cancer data: {}".format(cancer.data.shape))

Shape of cancer data: (569, 30)

cancer.target_names

array(['malignant', 'benign'], dtype='<U9')

• El conjunto de datos consta de 569 puntos de datos, con 30 características cada uno

print("Sample counts per class:\n{}".format(
{n: v for n, v in zip(cancer.target_names, np.bincount(cancer.target))}))

Sample counts per class:
{'malignant': 212, 'benign': 357}

• De estos 569 puntos de datos, 212 están etiquetados como malignos y 357 como benignos. Para obtener una descripción del significado semántico de cada característica, podemos echar un vistazo a el atributo feature_names. Si está interesado, puede obtener más información sobre los datos leyendo cancer.DESCR. Para mas información acerca de este conjunto de datos (ver Breast cancer wisconsin (diagnostic) dataset)

cancer.DESCR

'.. _breast_cancer_dataset:\n\nBreast cancer wisconsin (diagnostic) dataset\n--------------------------------------------\n\n**Data Set Characteristics:**\n\n:Number of Instances: 569\n\n:Number of Attributes: 30 numeric, predictive attributes and the class\n\n:Attribute Information:\n    - radius (mean of distances from center to points on the perimeter)\n    - texture (standard deviation of gray-scale values)\n    - perimeter\n    - area\n    - smoothness (local variation in radius lengths)\n    - compactness (perimeter^2 / area - 1.0)\n    - concavity (severity of concave portions of the contour)\n    - concave points (number of concave portions of the contour)\n    - symmetry\n    - fractal dimension ("coastline approximation" - 1)\n\n    The mean, standard error, and "worst" or largest (mean of the three\n    worst/largest values) of these features were computed for each image,\n    resulting in 30 features.  For instance, field 0 is Mean Radius, field\n    10 is Radius SE, field 20 is Worst Radius.\n\n    - class:\n            - WDBC-Malignant\n            - WDBC-Benign\n\n:Summary Statistics:\n\n===================================== ====== ======\n                                        Min    Max\n===================================== ====== ======\nradius (mean):                        6.981  28.11\ntexture (mean):                       9.71   39.28\nperimeter (mean):                     43.79  188.5\narea (mean):                          143.5  2501.0\nsmoothness (mean):                    0.053  0.163\ncompactness (mean):                   0.019  0.345\nconcavity (mean):                     0.0    0.427\nconcave points (mean):                0.0    0.201\nsymmetry (mean):                      0.106  0.304\nfractal dimension (mean):             0.05   0.097\nradius (standard error):              0.112  2.873\ntexture (standard error):             0.36   4.885\nperimeter (standard error):           0.757  21.98\narea (standard error):                6.802  542.2\nsmoothness (standard error):          0.002  0.031\ncompactness (standard error):         0.002  0.135\nconcavity (standard error):           0.0    0.396\nconcave points (standard error):      0.0    0.053\nsymmetry (standard error):            0.008  0.079\nfractal dimension (standard error):   0.001  0.03\nradius (worst):                       7.93   36.04\ntexture (worst):                      12.02  49.54\nperimeter (worst):                    50.41  251.2\narea (worst):                         185.2  4254.0\nsmoothness (worst):                   0.071  0.223\ncompactness (worst):                  0.027  1.058\nconcavity (worst):                    0.0    1.252\nconcave points (worst):               0.0    0.291\nsymmetry (worst):                     0.156  0.664\nfractal dimension (worst):            0.055  0.208\n===================================== ====== ======\n\n:Missing Attribute Values: None\n\n:Class Distribution: 212 - Malignant, 357 - Benign\n\n:Creator:  Dr. William H. Wolberg, W. Nick Street, Olvi L. Mangasarian\n\n:Donor: Nick Street\n\n:Date: November, 1995\n\nThis is a copy of UCI ML Breast Cancer Wisconsin (Diagnostic) datasets.\nhttps://goo.gl/U2Uwz2\n\nFeatures are computed from a digitized image of a fine needle\naspirate (FNA) of a breast mass.  They describe\ncharacteristics of the cell nuclei present in the image.\n\nSeparating plane described above was obtained using\nMultisurface Method-Tree (MSM-T) [K. P. Bennett, "Decision Tree\nConstruction Via Linear Programming." Proceedings of the 4th\nMidwest Artificial Intelligence and Cognitive Science Society,\npp. 97-101, 1992], a classification method which uses linear\nprogramming to construct a decision tree.  Relevant features\nwere selected using an exhaustive search in the space of 1-4\nfeatures and 1-3 separating planes.\n\nThe actual linear program used to obtain the separating plane\nin the 3-dimensional space is that described in:\n[K. P. Bennett and O. L. Mangasarian: "Robust Linear\nProgramming Discrimination of Two Linearly Inseparable Sets",\nOptimization Methods and Software 1, 1992, 23-34].\n\nThis database is also available through the UW CS ftp server:\n\nftp ftp.cs.wisc.edu\ncd math-prog/cpo-dataset/machine-learn/WDBC/\n\n.. dropdown:: References\n\n  - W.N. Street, W.H. Wolberg and O.L. Mangasarian. Nuclear feature extraction\n    for breast tumor diagnosis. IS&T/SPIE 1993 International Symposium on\n    Electronic Imaging: Science and Technology, volume 1905, pages 861-870,\n    San Jose, CA, 1993.\n  - O.L. Mangasarian, W.N. Street and W.H. Wolberg. Breast cancer diagnosis and\n    prognosis via linear programming. Operations Research, 43(4), pages 570-577,\n    July-August 1995.\n  - W.H. Wolberg, W.N. Street, and O.L. Mangasarian. Machine learning techniques\n    to diagnose breast cancer from fine-needle aspirates. Cancer Letters 77 (1994)\n    163-171.\n'

print("Feature names:\n{}".format(cancer.feature_names))

Feature names:
['mean radius' 'mean texture' 'mean perimeter' 'mean area'
 'mean smoothness' 'mean compactness' 'mean concavity'
 'mean concave points' 'mean symmetry' 'mean fractal dimension'
 'radius error' 'texture error' 'perimeter error' 'area error'
 'smoothness error' 'compactness error' 'concavity error'
 'concave points error' 'symmetry error' 'fractal dimension error'
 'worst radius' 'worst texture' 'worst perimeter' 'worst area'
 'worst smoothness' 'worst compactness' 'worst concavity'
 'worst concave points' 'worst symmetry' 'worst fractal dimension']

• También utilizaremos un conjunto de datos de regresión del mundo real, el conjunto de datos Boston Housing. La tarea asociada a este conjunto de datos consiste en predecir el valor medio de las viviendas en varios barrios de Boston en la década de 1970, utilizando información como el índice de criminalidad, la proximidad al río Charles, la accesibilidad a las autopistas, etc. El dataset contiene 506 puntos de datos, descritos por 13 características

import pandas as pd
import numpy as np

data_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None)
data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
target = raw_df.values[1::2, 2]
print("Data shape: {}".format(data.shape))

Data shape: (506, 13)

• Para nuestro propósito, vamos a ampliar este conjunto de datos, no sólo 13 mediciones como características de entrada serán consideradas, sino también observando todos los productos (también llamados interactions) entre las características. En otras palabras, no sólo consideraremos la tasa de criminalidad y la accesibilidad a las carreteras como características, sino que también, el producto entre la tasa de criminalidad y la accesibilidad a las carreteras.

• La inclusión de características derivadas como éstas se denomina ingeniería de características (feature engineering), de la que hablaremos en secciones posteriores. Este conjunto de datos derivados puede ser cargado con la función load_extended_boston

X, y = mglearn.datasets.load_extended_boston()
print("X.shape: {}".format(X.shape))

X.shape: (506, 104)

• Las 104 características resultantes son las 13 características originales junto con las 91 combinaciones posibles de dos características dentro de esas 13. Utilizaremos estos conjuntos de datos para explicar e ilustrar las propiedades de los distintos algoritmos de aprendizaje automático. Pero por ahora, vamos a hablar de los algoritmos en sí. En primer lugar, vamos a examinar el algoritmo de los vecinos más cercanos (k-nearest neighbors) (k-NN).