7. PCA

7.1. Análisis

Introducción

• El Análisis de Componentes Principales (PCA) es un método para consolidar las variables mutuamente correlacionadas de datos observados multidimensionales en nuevas variables mediante combinaciones lineales de las variables originales con una pérdida mínima de información en los datos observados.

• PCA permite extraer información relevante de los datos al fusionar múltiples variables que caracterizan a los individuos. También se puede utilizar como técnica para comprender visualmente las estructuras de datos al consolidar datos de alta dimensión en un número menor de variables, realizando una reducción de dimensión y proyectando los resultados en una línea unidimensional, plano bidimensional o espacio tridimensional.

• En este capítulo se discuten los conceptos básicos y el propósito de PCA en el contexto de la linealidad, así como su aplicación en la descompresión de imágenes y la descomposición de valores singulares de matrices de datos. También se aborda el PCA no lineal utilizando el método del kernel para la extracción de información de datos multidimensionales con estructuras no lineales complejas.

7.2. Concepto básico

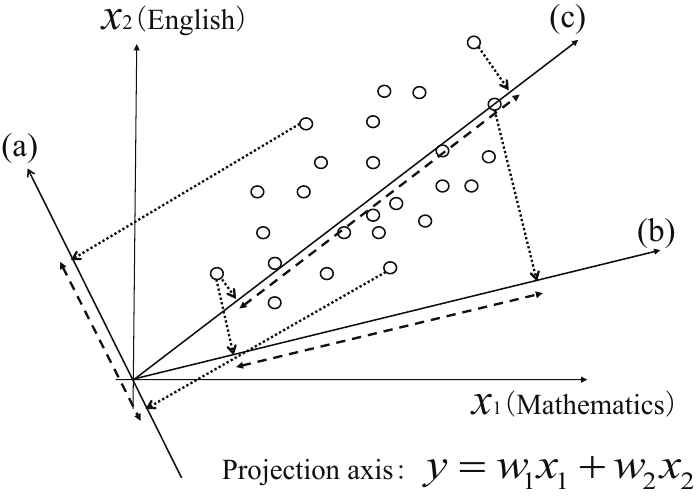
Fig. 7.1 Proyección en tres ejes diferentes, (a), (b) y (c), y la dispersión de los datos. Fuente [Konishi, 2014].

• La Fig. 7.1 muestra un gráfico de las puntuaciones de los exámenes de matemáticas (\(x_{1}\)) e inglés (\(x_{2}\)) de 25 estudiantes. Proyectando estos datos bidimensionales en un solo eje mediante la sustitución de las puntuaciones de ambas materias en la siguiente ecuación, se transforman en datos unidimensionales.

  \[ y=w_{1}x_{1}+w_{2}x_{2}. \]

• La Fig. 7.1 muestra la proyección en tres ejes diferentes, (a), (b) y (c). La dispersión de los datos (como medida de la varianza) para cada eje se indica mediante una flecha de doble cabeza (\(\boldsymbol{\leftarrow-\rightarrow}\)).

Observación

• Esta figura muestra que la varianza es mayor cuando se proyecta en el eje (b) que en el eje (a), y mayor en el eje (c) que en el eje (b). El eje con mayor varianza muestra con mayor claridad la separación entre los datos. Surge la pregunta inmediata de cómo encontrar mejor el eje de proyección que produce la máxima varianza.

• En PCA, utilizamos una secuencia de ejes de proyección con este propósito.

  • Primero encontramos el eje de proyección, conocido como el primer componente principal, que maximiza la varianza global.

  • Luego encontramos el eje de proyección que maximiza la varianza bajo la restricción de ortogonalidad al primer componente principal. Este eje se conoce como el segundo componente principal.

  • La ortogonalidad entre las componentes principales en PCA garantiza una representación óptima de la variabilidad de los datos, lo que facilita la interpretación y el análisis de los mismos.

• Apliquemos lo mencionado en la anterior observación a datos bidimensionales. Denotamos los \(n\) datos observados bidimensionales \(\boldsymbol{x}=(x_{1}, x_{2})^{T}\) como

(7.1)\[\begin{split} \boldsymbol{x}_{1}=\begin{pmatrix}x_{11}\\x_{12}\end{pmatrix},~\boldsymbol{x}_{2}=\begin{pmatrix}x_{21}\\x_{22}\end{pmatrix},\dots,\boldsymbol{x}_{n}=\begin{pmatrix}x_{n1}\\x_{n2}\end{pmatrix}. \end{split}\]

• Estos \(n\) datos bidimensionales se proyectan sobre \(y=w_{1}x_{1}+w_{2}x_{2}\), y luego se expresan como

  \[ y_{i}=w_{1}x_{i1}+w_{2}x_{i2}=\boldsymbol{w}^{T}\boldsymbol{x}_{i},~i=1,2,\dots,n, \]

  donde \(\boldsymbol{w}=(w_{1}, w_{2})^{T}\) representa un vector de coeficientes.

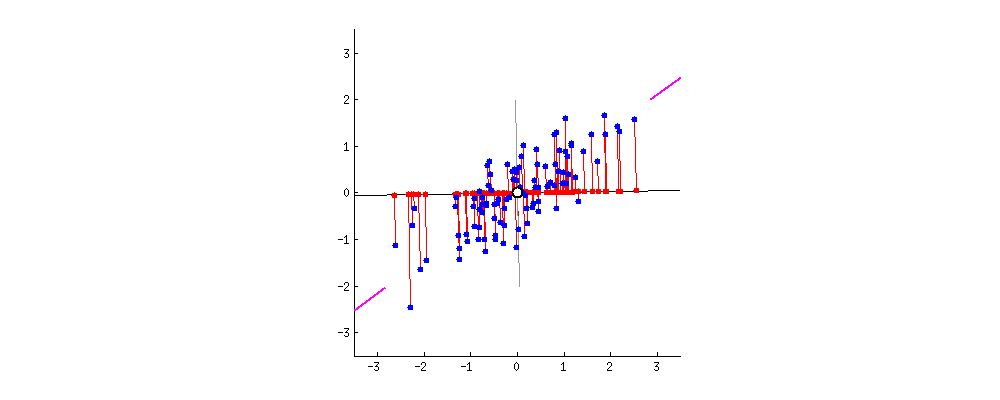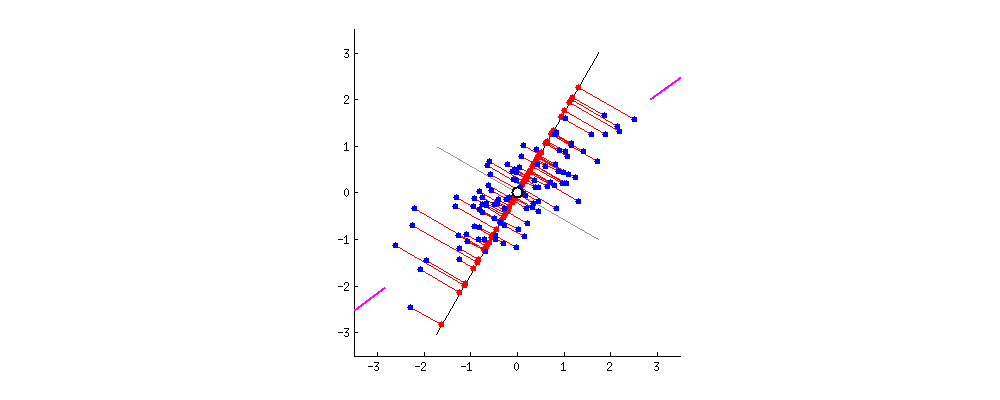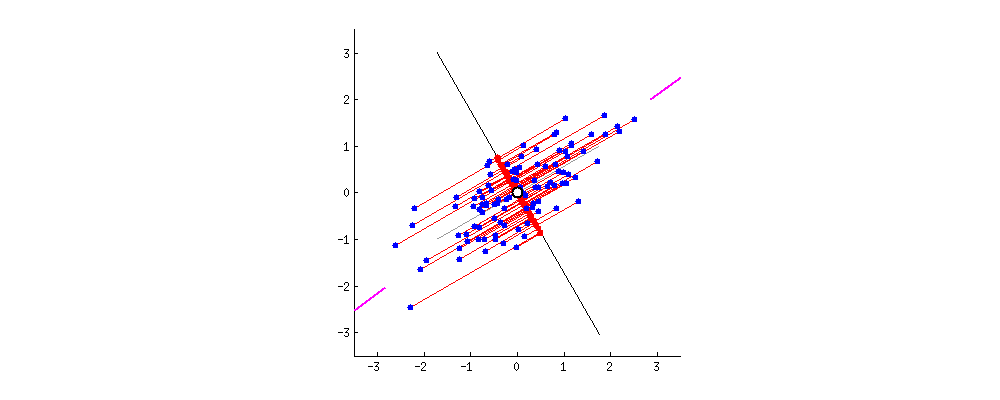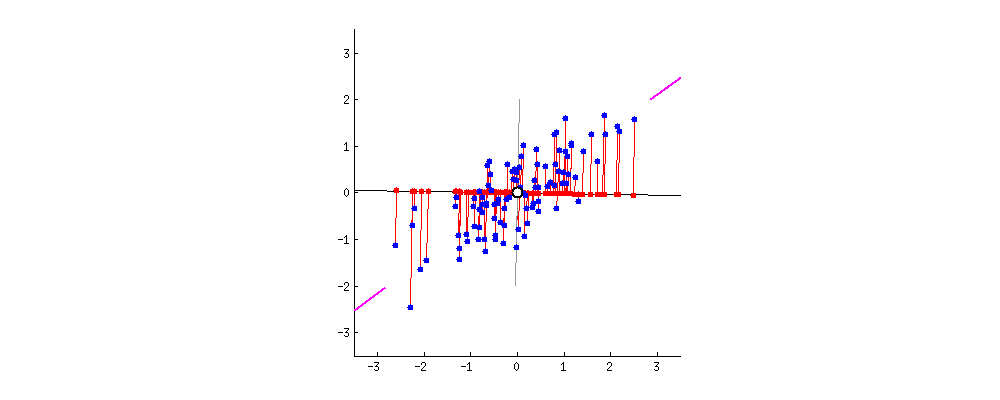
Fig. 7.2 Simulación de múltiples ejes de proyección \(y=w_{1}x_{1}+w_{2}x_{2}\) en el PCA.

Datos proyectados repetidos?

• Es posible que los datos proyectados en las componentes principales sean repetidos en ciertas circunstancias, especialmente cuando los datos originales tienen una alta dimensionalidad o cuando hay baja variabilidad en algunas dimensiones.

• Esto es importante tener en cuenta al interpretar los resultados de PCA y al realizar análisis subsiguientes. Cuando esto ocurre, puedes considerar las siguientes estrategias:

  • Normalización de los datos

  • Reducción de multicolinealidad

  • Usar Análisis de Factores

• La media de los datos \(y_{1}, y_{2}, \dots, y_{n}\) que se proyectan sobre el eje de proyección es

  \[ \overline{y}=\frac{1}{n}\sum_{i=1}^{n}y_{i}=\frac{1}{n}\sum_{i=1}^{n}(w_{1}x_{i1}+w_{2}x_{i2})=w_{1}\overline{x}_{1}+w_{2}\overline{x}_{2}=\boldsymbol{w}\overline{\boldsymbol{x}}, \]

  donde \(\overline{\boldsymbol{x}}=(\overline{x}_{1}, \overline{x}_{2})^{T}\) es el vector de medias muestrales que contiene como sus componentes principales la media muestral \(\overline{x}_{j}=n^{-1}\sum_{i=1}^{n}x_{ij}~(j=1,2)\) de cada variable.

• La varianza puede ser expresada como

  (7.2)\[\begin{split} \begin{align*} s_{y}^{2} &= \frac{1}{n}\sum_{i=1}^{n}(y_{i}-\overline{y})^{2}\\ &= \frac{1}{n}\sum_{i=1}^{n}\left\{w_{1}(x_{i1}-\overline{x}_{1})+w_{2}(x_{i2}-\overline{x}_{2})\right\}^{2}\\ &= w_{1}^{2}\frac{1}{n}\sum_{i=1}^{n}(x_{i1}-\overline{x}_{1})^{2}+2w_{1}w_{2}\frac{1}{n}\sum_{i=1}^{n}(x_{i1}-\overline{x}_{1})(x_{i2}-\overline{x}_{2})+w_{2}^{2}\frac{1}{n}\sum_{i=1}^{n}(x_{i2}-\overline{x}_{2})^{2}\\[1mm] &= w_{1}^{2}s_{11}+2w_{1}w_{2}s_{12}+w_{2}^{2}s_{22}\\[4mm] &= \boldsymbol{w}^{T}S\boldsymbol{w}, \end{align*} \end{split}\]

  donde \(S\) es la matriz de covarianza muestral, definida por (verifíquelo)

  (7.3)\[\begin{split} S=\begin{pmatrix}s_{11} & s_{12}\\s_{21} & s_{22}\end{pmatrix},~s_{jk}=\frac{1}{n}\sum_{i=1}^{n}(x_{ij}-\overline{x}_{j})(x_{ik}-\overline{x}_{k}),~j,k=1,2. \end{split}\]

Maximización de la varianza

• El problema de encontrar el vector de coeficientes \(\boldsymbol{w}=(w_{1}, w_{2})^{T}\), que corresponde a la máxima varianza para los \(n\) datos bidimensionales proyectados sobre \(y=w_{1}x_{1}+w_{2}x_{2}\), se convierte en el problema de maximización de la varianza \(S_{y}=\boldsymbol{w}^{T}S\boldsymbol{w}\) en la Ecuación (7.2) bajo la restricción \(\boldsymbol{w}^{T}\boldsymbol{w}=1\). Esta restricción se aplica porque \(\|\boldsymbol{w}\|\) sería infinitamente grande sin ella y la varianza divergiría.

• El problema de maximización de la varianza bajo esta restricción se puede resolver mediante el método de los multiplicadores de Lagrange, encontrando el punto estacionario (donde la derivada se hace 0) de la función Lagrangiana.

\[ L(\boldsymbol{w}, \lambda)=\boldsymbol{w}^{T}S\boldsymbol{w}+\lambda(1-\boldsymbol{w}^{T}\boldsymbol{w}) \]

• Dado que \(\partial(\boldsymbol{w}^{T}S\boldsymbol{w})/\partial\boldsymbol{w}=2S\boldsymbol{w}\) (ver Ecuación (3.9)) y \(\partial(\boldsymbol{w}^{T}\boldsymbol{w})/\partial\boldsymbol{w}=2\boldsymbol{w}\), entonces \(\partial L(\boldsymbol{w}, \lambda)/\partial\boldsymbol{w}=0\) sii

  (7.4)\[ S\boldsymbol{w}=\lambda\boldsymbol{w}. \]

• Esta solución es el vector propio \(\boldsymbol{w}_{1}=(w_{11}, w_{12})^{T}\) correspondiente al valor propio máximo \(\lambda_{1}\) obtenido al resolver la ecuación característica para la matriz de varianza-covarianza de la muestra \(S\). Por consiguiente, el primer componente principal \(y_{1}\) está dado por

  \[ y_{1}=w_{11}x_{1}+w_{12}x_{2}=\boldsymbol{w}_{1}^{T}\boldsymbol{x}. \]

• La varianza del primer componente principal \(y_{1}\) se alcanza con \(\boldsymbol{w}=\boldsymbol{w}_{1}\), el cual maximiza la varianza de la Ecuación (7.2), y es, por lo tanto,

  (7.5)\[ s_{y_{1}}^{2}=\boldsymbol{w}_{1}^{T}S\boldsymbol{w}_{1}=\lambda_{1}. \]

• Nótese que, la (7.5) es obtenida gracias a la relación entre autovalor-autovector \(S\boldsymbol{w}_{1}=\lambda_{1}\boldsymbol{w}_{1}\) de la matriz simétrica \(S\), y que el vector \(\boldsymbol{w}_{1}\) es normalizado a longitud 1 (verifíquelo).

• El segundo componente principal, al proyectar los datos bidimensionales en \(y=w_{1}x_{1}+w_{2}x_{2}\) bajo la restricción de normalización \(\boldsymbol{w}\boldsymbol{w}^{T}=1\) junto con la ortogonalidad al primer componente principal, se define como el vector de coeficientes que maximiza la varianza \(S_{y_{2}}^{2}=\boldsymbol{w}^{T}S\boldsymbol{w}\) con \(\boldsymbol{w}_{1}^{T}\boldsymbol{w}=0\).

• La solución, de la misma manera que para el primer componente principal, se obtiene como el punto estacionario respecto a \(\boldsymbol{w}\) para la función Lagrangiana

  \[ L(\boldsymbol{w}, \lambda, \gamma)=\boldsymbol{w}^{T}S\boldsymbol{w}+\lambda(1-\boldsymbol{w}^{T}\boldsymbol{w})+\gamma\boldsymbol{w}_{1}^{T}\boldsymbol{w}, \]

  donde \(\lambda, \gamma\) son multiplicadores de Lagrange.

• Cuando diferenciamos parcialmente la ecuación anterior respecto a \(\boldsymbol{w}\) y establecemos el resultado igual a 0 (\(\partial_{\boldsymbol{w}}L=\boldsymbol{0}\)), obtenemos la ecuación

  (7.6)\[ \frac{\partial L(\boldsymbol{w},\lambda, \gamma)}{\partial\boldsymbol{w}}=0\Leftrightarrow 2S\boldsymbol{w}-2\lambda w+\gamma\boldsymbol{w}_{1}=\boldsymbol{0}. \]

• Si luego multiplicamos a la izquierda por el vector propio \(\boldsymbol{w}_{1}^{T}\) correspondiente al valor propio máximo \(\lambda_{1}\), obtenemos

  \[\begin{split} \begin{align*} 2\boldsymbol{w}_{1}^{T}S\boldsymbol{w}-2\lambda\textcolor{red}{\boldsymbol{w}_{1}^{T}\boldsymbol{w}}+\gamma\textcolor{red}{\boldsymbol{w}_{1}^{T}\boldsymbol{w}_{1}} &= 0\Leftrightarrow\begin{cases}\boldsymbol{w}_{1}^{T}\boldsymbol{w}&=0\\\boldsymbol{w}_{1}^{T}\boldsymbol{w}_{1}&=1\end{cases}\\ 2\textcolor{red}{\boldsymbol{w}_{1}^{T}S}\boldsymbol{w}+\gamma &= 0\Leftrightarrow (S\boldsymbol{w}_{1}=\lambda_{1}\boldsymbol{w}_{1}\Leftrightarrow\boldsymbol{w}_{1}^{T}S=\lambda_{1}\boldsymbol{w}_{1}^{T})\\[3mm] 2\textcolor{red}{\lambda\boldsymbol{w}_{1}^{T}}\boldsymbol{w}+\gamma &= 0\Leftrightarrow\\[3mm] \gamma &=0 \end{align*} \end{split}\]

• Entonces la Ecuación (7.6) se convierte en

  (7.7)\[\begin{split} 2Sw-2\lambda\boldsymbol{w}+\gamma\boldsymbol{w}_{1}=2S\boldsymbol{w}-2\lambda\boldsymbol{2}=0\Leftrightarrow S\boldsymbol{w}=\lambda\boldsymbol{w},~\text{donde}~\begin{cases}\boldsymbol{w}_{1}^{T}\boldsymbol{w}&=0\\\boldsymbol{w}_{1}^{T}\boldsymbol{w}_{1}&=1\end{cases} \end{split}\]

• La solución del problema de autovalores y autovectores asociado a la Ecuación (7.7) entrega el par autovector/autovalor \((\lambda_{2}, \boldsymbol{w}_{2})\), donde \(\boldsymbol{w}_{2}=(w_{21}, w_{22})^{T}\).

• El segundo componente principal puede ser dado por la siguiente ecuación

  \[ y_{2}=w_{21}x_{1}+w_{22}x_{2}=\boldsymbol{w}_{2}^{T}\boldsymbol{x} \]

• De la relación entre el autovalor y el autovector de la matriz simétrica \(S\), la varianza del segundo componente principal \(y_{2}\) se convierte en \(s_{y_{2}}^{2}=\boldsymbol{w}_{2}S\boldsymbol{w}_{2}=\lambda_{2}\) de la misma manera que en la Ecuación (7.5).

• El PCA basado en los datos bidimensionales en Ecuación (7.1) es esencialmente un problema de encontrar los autovalores y autovectores de la matriz de varianza-covarianza muestral \(S\).

Observación

• Dado que cada componente principal captura una parte única de la variabilidad en los datos, cada una contiene información diferente sobre la estructura de los datos originales. Esto significa que, mientras más componentes principales tengamos, más información detallada obtenemos sobre la distribución de los datos en el espacio de características.

7.3. Autovalores, Autovectores y Componentes Principales

• Denotamos los autovalores de la matriz de varianza-covarianza muestral \(S\) en orden descendente según su magnitud como \(\lambda_{1}\geq\lambda_{2}\geq0\), y los correspondientes autovectores mutuamente ortogonales normalizados a longitud 1 como \(\boldsymbol{w}_{1}=(w_{11}, w_{12})^{T}\) y \(\boldsymbol{w}_{2}=(w_{21}, w_{22})^{T}\).

• Los primeros y segundos componentes principales y sus respectivas varianzas se dan entonces de la siguiente manera

  \[\begin{split} \begin{align*} y_{1} &= w_{11}x_{1}+w_{12}x_{2},\quad\text{var}(y_{1})=\lambda_{1}\\ y_{2} &= w_{21}x_{1}+w_{22}x_{2},\quad\text{var}(y_{2})=\lambda_{2} \end{align*} \end{split}\]

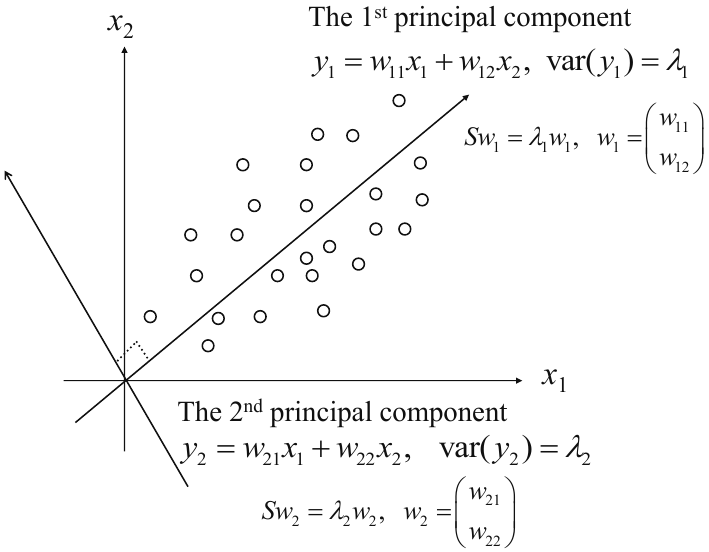
Fig. 7.3 Valores propios, primeros y segundos componentes principales. Fuente [Konishi, 2014].

• El método de los multiplicadores de Lagrange, como se utiliza en esta sección, proporciona una herramienta para encontrar los puntos estacionarios de funciones multivariables de valores reales bajo restricciones de igualdad y desigualdad en las variables.

7.4. Proceso de Derivación de Componentes Principales y Propiedades

• En general, denotamos como \(\boldsymbol{x}=(x_{1}, x_{2},\dots,x_{p})^{T}\) las \(p\) variables representando las características individuales. Basados en los datos observados \(\boldsymbol{x}_{1}, \boldsymbol{x}_{2},\dots, \boldsymbol{x}_{n}\); \(p\)-dimensionales, para las \(p\) variables, obtenemos la matriz de varianza-covarianza muestral

  (7.8)\[ S=(s_{jk})=\frac{1}{n}\sum_{i=1}^{n}(\boldsymbol{x}_{i}-\overline{\boldsymbol{x}})(\boldsymbol{x}_{i}-\boldsymbol{x})^{T} \]

  donde \(\overline{\boldsymbol{x}}\) es el vector de medias muestrales, \(p\)-dimensional, y \(s_{jk}=\sum_{i=1}^{n}(x_{ij}-\overline{x}_{j})(x_{ik}-\overline{x}_{k})/n\) (escriba cada componente de \(S\) en forma matricial).

• Siguiendo el concepto básico de la derivación de componentes principales, como se describe para datos bidimensionales en la sección anterior, primero proyectamos los \(n\) datos observados, \(p\)-dimensionales sobre el eje de proyección

  (7.9)\[ y=w_{1}x_{1}+w_{2}x_{2}+\cdots+w_{p}x_{p}=\boldsymbol{w}^{T}\boldsymbol{x}, \]

  y obtenemos los datos unidimensionales \(y_{i}=\boldsymbol{w}^{T}\boldsymbol{x}_{i}~(i=1,2,\dots,n;~\boldsymbol{x}_{i}~p\text{-dimensional})\).

• La media de los datos proyectados, representada por \(\overline{y}=n^{-1}\sum_{i=1}^{n}\boldsymbol{w}^{T}\boldsymbol{x}_{i}=\boldsymbol{w}^{T}\overline{\boldsymbol{x}}\) (escriba el vector de componentes de \(\overline{\boldsymbol{x}}\)) permite expresar la varianza como:

  \[\begin{split} \begin{align*} s_{y}^{2} &= \frac{1}{n}\sum_{i=1}^{n}(y_{i}-\overline{y})^{2}\\ &= \frac{1}{n}\sum_{i=1}^{n}(\boldsymbol{w}^{T}\boldsymbol{x}_{i}-\boldsymbol{w}^{T}\overline{\boldsymbol{x}})^{2}\\ &= \frac{1}{n}\sum_{i=1}^{n}(\boldsymbol{w}^{T}(\boldsymbol{x}_{i}-\overline{\boldsymbol{x}}))(\boldsymbol{w}^{T}(\boldsymbol{x}_{i}-\overline{\boldsymbol{x}}))^{T}\\ &= \boldsymbol{w}^{T}\frac{1}{n}\sum_{i=1}^{n}(\boldsymbol{x}_{i}-\overline{\boldsymbol{x}})(\boldsymbol{x}_{i}-\overline{\boldsymbol{x}})^{T}\boldsymbol{w}\\ &= \boldsymbol{w}^{T}S\boldsymbol{w}. \end{align*} \end{split}\]

• De manera similar a lo aplicado en dos dimensiones, el vector de coeficientes que maximiza la varianza de los datos proyectados puede expresarse como el autovector \(\boldsymbol{w}_{1}\) correspondiente al mayor autovalor \(\lambda_{1}\) de la matriz de varianza-covarianza muestral \(S\).

• El eje de proyección \(y_{1}=\boldsymbol{w}_{1}^{T}\boldsymbol{x}\) con \(\boldsymbol{w}_{1}\) como vector de coeficientes es entonces el primer componente principal. De la misma manera, nuevamente, la varianza en este eje de proyección es el mayor autovalor \(\lambda_{1}\)

• El segundo componente principal es el eje que, cumpliendo con la ortogonalidad al primer componente principal, maximiza la varianza de los datos proyectados \(p\)-dimensionales, y, por lo tanto, es el eje de proyección generado por el autovector \(\boldsymbol{w}_{2}\), que corresponde al segundo mayor autovalor \(\lambda_{2}\) de la matriz \(S\)

Observación

• Continuando de la misma manera, el tercer componente principal se define como el eje que, cumpliendo con la ortogonalidad al primer y segundo componente principal, maximiza la varianza de los datos proyectados \(p\)-dimensionales. Repitiendo sucesivamente este proceso, podemos en principio derivar \(p\) componentes principales para las combinaciones lineales de las variables originales.

• La invertibilidad de la matriz de covarianza en PCA se garantiza debido a la necesidad de que las variables originales sean linealmente independientes, lo que conduce a una matriz de covarianza no singular.

• Como resultado, PCA se convierte así en el problema de los autovalores de la matriz de varianza-covarianza muestral \(S\), como se describe a continuación.

7.4.1. El problema de los autovalores de la matriz de varianza-covarianza muestral y los componentes principales

• Denotemos \(S\) como una matriz de varianza-covarianza muestral basada en \(n\) datos observados \(p\)-dimensionales. Como se observa en la Ecuación (7.8), es una matriz simétrica de orden \(p\). Luego, denotamos los \(p\) autovalores

  \[ \lambda_{1}\geq\lambda_{2}\geq\cdots\lambda_{i}\geq\cdots\geq\lambda_{p}\geq0, \]

  dados como la solución a la ecuación característica de \(S,~|S-\lambda I_{p}|=0\).

• Además, denotamos los autovectores \(p\)-dimensionales normalizados a longitud 1 correspondientes a estos autovalores como

  \[\begin{split} \boldsymbol{w}_{1}= \begin{pmatrix} w_{11}\\ w_{12}\\ \vdots\\ w_{1p} \end{pmatrix},~ \boldsymbol{w}_{2}= \begin{pmatrix} w_{21}\\ w_{22}\\ \vdots\\ w_{2p} \end{pmatrix},\dots, \boldsymbol{w}_{p}= \begin{pmatrix} w_{p1}\\ w_{p2}\\ \vdots\\ w_{pp} \end{pmatrix} \end{split}\]

• Para estos autovectores, la normalización \(\boldsymbol{w}_{i}^{T}\boldsymbol{w}_{i}=1\) para longitud del vector 1 y la ortogonalidad \(\boldsymbol{w}_{i}^{T}\boldsymbol{w}_{j}=0\) (para \(i\neq j\)) quedan así establecidas.

• Los \(p\) componentes principales y su varianza expresada en términos de la combinación lineal de las variables originales pueden ser proporcionados en orden de la siguiente manera

  (7.10)\[\begin{split} \begin{align*} y_{1} &= w_{11}x_{1}+w_{12}x_{2}+\cdots+w_{1p}x_{p}=\boldsymbol{w}_{1}^{T}\boldsymbol{x},\quad\text{var}(y_{1})=\lambda_{1},\\ y_{2} &= w_{21}x_{1}+w_{22}x_{2}+\cdots+w_{2p}x_{p}=\boldsymbol{w}_{2}^{T}\boldsymbol{x},\quad\text{var}(y_{2})=\lambda_{2},\\ &\vdots\\ y_{p} &= w_{p1}x_{1}+w_{p2}x_{2}+\cdots+w_{pp}x_{p}=\boldsymbol{w}_{p}^{T}\boldsymbol{x},\quad\text{var}(y_{p})=\lambda_{p}. \end{align*} \end{split}\]

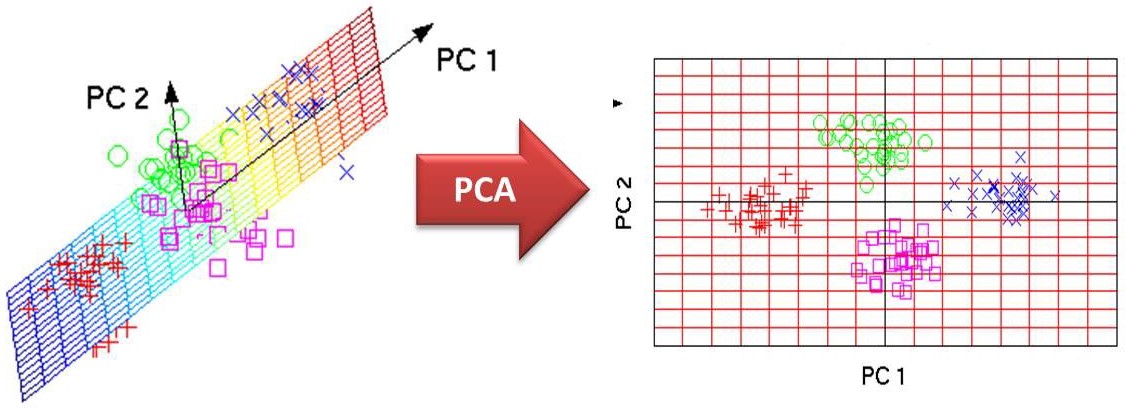
Reducción de dimensión

• Al aplicar \(PCA\), es posible reducir la dimensionalidad de los \(n\) datos observados \(p\)-dimensionales

  \[ \{\boldsymbol{x}_{i}=(x_{i1}, x_{i2}, \dots, x_{ip})^{T}:~i=1,2,\dots, n\} \]

  para las \(p\) variables originales a un número menor, utilizando solo los primeros componentes principales; por ejemplo, a datos bidimensionales

  \[ \{(y_{i1}, y_{i2}):~i=1,2,\dots,n\} \]

  utilizando solo el primero y el segundo componente principal, donde \(y_{i1}=\boldsymbol{w}_{1}^{T}\boldsymbol{x}_{i}\), \(y_{i2}=\boldsymbol{w}_{2}^{T}\boldsymbol{x}_{i}\)

• Al proyectar así el conjunto de datos del espacio de dimensiones superior sobre un plano bidimensional, podemos aprender visualmente la estructura de los datos. Al encontrar el significado de las nuevas variables combinadas como combinaciones lineales de las variables originales, además, podemos extraer información útil.

• El significado de los componentes principales puede entenderse en términos de la magnitud y el signo de los coeficientes \(w_{ij}\) de cada variable. Además, la correlación entre los componentes principales y las variables como indicador cuantitativo es muy útil para identificar las variables que influyen en los componentes principales. La correlación entre el \(i\)-ésimo componente principal \(y_{i}\) y la variable \(x_{j}\) está dada por

  \[ r_{y_{i}, x_{j}}=\frac{\text{cov}(y_{i}, x_{j})}{\sqrt{\text{var}(y_{i})}\sqrt{\text{var}(x_{j})}}= \frac{\lambda_{i}w_{ij}}{\sqrt{\lambda_{i}}\sqrt{s_{jj}}}=\frac{\sqrt{\lambda_{i}}w_{ij}}{\sqrt{s_{jj}}} \]

  donde \(\lambda_{i}\) es la varianza del \(i\)-ésimo componente principal, \(w_{ij}\) es el coeficiente de la variable \(x_{j}\) para el \(i\)-ésimo componente principal, y \(s_{jj}\) es la varianza de la variable \(x_{j}\).

Observación (Reducción de dimensionalidad)

• ¿Cuántas componentes principales son necesarias?: Trazar un gráfico de la varianza explicada acumulativa en función del número de componentes y seleccionar el número de componentes que capturan una cantidad significativa de la varianza total (por ejemplo, el 70% o el 80%).

• El 70% o 80% de varianza explicada es un umbral comúnmente utilizado en PCA para determinar el número de componentes principales que se deben retener en un modelo. Al retener el 70% o 80% de la varianza, se conserva la mayor parte de la información importante en los datos originales, y generalmente, conservar este porcentaje implica una reducción relevante en la dimensionalidad de los datos.

7.5. Autovalores y autovectores de una matriz simétrica

• La matriz de varianza-covarianza muestral \(S\) dada por la Ecuación (7.8) es una matriz simétrica de orden \(p\), con la siguiente relación entre sus autovalores y autovectores

  (7.11)\[ S\boldsymbol{w}_{i}=\lambda_{i}\boldsymbol{w}_{i},~\boldsymbol{w}_{i}^{T}\boldsymbol{w}_{i}=1,~\boldsymbol{w}_{i}^{T}\boldsymbol{w}_{j}=0~(i\neq j) \]

  para \(i,j=1,2,\dots,p\).

• Denotamos como \(W\) la matriz de orden \(p\) que tiene como columnas los \(p\) autovectores, y como \(\Lambda\) la matriz de orden \(p\) que tiene los autovalores como sus elementos diagonales, es decir,

  \[\begin{split} W=(\boldsymbol{w}_{1}, \boldsymbol{w}_{2}, \dots, \boldsymbol{w}_{p}),~ \Lambda = \begin{pmatrix} \lambda_{1} & 0 & \cdots & 0\\ 0 & \lambda_{2} & \cdots & 0\\ \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & \vdots & \lambda_{p} \end{pmatrix} \end{split}\]

• La relación entre los autovalores y autovectores de la matriz de varianza-covarianza muestral \(S\) dada por Ecuación (7.11) puede expresarse de la siguiente manera (verifíquelo):

  1. \(SW=W\Lambda,\quad W^{T}W=I_{p}\)

  2. \(W^{T}SW=\Lambda\)

  3. \(S=W\Lambda W^{T}=\lambda_{1}\boldsymbol{w}_{1}\boldsymbol{w}_{1}^{T}+\lambda_{2}\boldsymbol{w}_{2}\boldsymbol{w}_{2}^{T}+\cdots+\lambda_{p}\boldsymbol{w}_{p}\boldsymbol{w}_{p}^{T}\)

  4. \(\text{tr}(S)=\text{tr}(W\Lambda W^{T})=\text{tr}(\Lambda)=\lambda_{1}+\lambda_{2}+\cdots+\lambda_{p}\)

Observación

• La Ecuación (2) muestra que la matriz simétrica \(S\) puede ser diagonalizada por la matriz ortogonal \(W\), y la Ecuación (3) es conocida como la descomposición espectral de la matriz simétrica \(S\).

• La Ecuación (4) muestra que la suma, \(\text{tr}(S)=s_{11}+s_{22}+\cdots+s_{pp}\), de las varianzas de las variables originales \(x_{1}, x_{2}, \dots, x_{p}\) es igual a la suma, \(\text{tr}(\Lambda)=\lambda_{1}+\lambda_{2}+\cdots+\lambda_{p}\), de las varianzas de los \(p\) componentes principales construidos.

7.6. Estandarización y matriz de correlación muestral

Introducción

• Supongamos que, además de las puntuaciones en matemáticas, inglés, ciencias y japonés, agregamos como quinta variable la proporción de respuestas correctas dadas para 100 problemas de cálculo que miden la habilidad para calcular y realizamos PCA basado en los datos resultantes de cinco dimensiones.

• En este caso, las unidades de medida difieren sustancialmente entre la proporción de respuestas correctas y las puntuaciones de las pruebas de materias, por lo que es necesario estandarizar los datos observados.

• Para los \(n\) datos observados \(p\) dimensionales

  (7.12)\[ \boldsymbol{x}_{i}=(x_{i1}, x_{i2}, \dots, x_{ip})^{T},\quad i=1, 2, \dots, n, \]

  Primero obtenemos el vector de media muestral \(\overline{\boldsymbol{x}}=(\overline{x}_{1}, \overline{x}_{2}, \dots, \overline{x}_{p})^{T}\) y la matriz de varianza-covarianza muestral \(S=(s_{jk})\). Estandarizamos los datos \(p\)-dimensionales en Ecuación (7.12) de manera que

  \[ \boldsymbol{z}_{i}=(z_{i1}, z_{i2}, \dots, z_{ip})^{T},\quad z_{ij}=\frac{x_{ij}-\overline{x}_{j}}{\sqrt{s_{jj}}},\quad j=1, 2, \dots, p. \]

• La varianza muestral (\(s_{jj}^{\star}\)) y la covarianza muestral (\(s_{jk}^{\star}\)) basadas en estos datos \(p\)-dimensionales estandarizados se dan entonces por

  \[ s_{jk}^{\star}=\frac{1}{n}\sum_{i=1}^{n}z_{ij}z_{ik}=\frac{1}{n}\sum_{i=1}^{n}\frac{(x_{ij}-\overline{x}_{j})(x_{ik}-\overline{x}_{k})}{\sqrt{s_{jj}}\sqrt{s_{kk}}}=\frac{s_{jk}}{\sqrt{s_{jj}}\sqrt{s_{kk}}}\equiv r_{jk} \]

  para \(j, k=1,2,\dots,p\).

Observación

• Nótese que en la matriz de varianza-covarianza muestral basada en los datos estandarizados, todos los elementos diagonales \(r_{jj}\) son 1, y obtenemos la matriz \(R\) con \(r_{jk}\) como los elementos no diagonales, los coeficientes de correlación muestral entre las variables \(j\)-ésima y \(k\)-ésima (matriz de correlación muestral).

• PCA comenzando con datos multidimensionales estandarizados se convierte así en un problema de encontrar los autovalores y autovectores de la matriz de correlación muestral \(R\), lo cual se realiza mediante el mismo proceso de derivación de componentes principales que el de PCA comenzando con una matriz de varianza-covarianza muestral (verifíquelo).

7.7. Reducción de dimensión y pérdida de información

Introducción

• En \(PCA\), la varianza proporciona una medida de información, y, por lo tanto, la pérdida de información puede ser estimada cuantitativamente a partir de los tamaños relativos de las varianzas de los componentes principales.

• Como se muestra en Ecuación (7.10), la varianza del componente principal está dada por el autovalor de la matriz de varianza-covarianza muestral.

• En resumen, podemos utilizar \(\lambda_{1}/(\lambda_{1}+\lambda_{2}+\cdots+\lambda_{p})\) para evaluar qué proporción de la información contenida en las \(p\) variables originales está presente en el primer componente principal \(y_{1}\).

• En general, la siguiente ecuación se utiliza como medida de la información presente en el \(i\)-ésimo componente principal \(y_{i}\)

  \[ \frac{\lambda_{i}}{\lambda_{1}+\lambda_{2}+\cdots+\lambda_{p}}. \]

• De manera similar, el porcentaje de varianza explicada por los primeros \(k\) componentes principales se calcula mediante:

\[ \frac{\lambda_{1}+\lambda_{2}+\cdots+\lambda_{k}}{\lambda_{1}+\lambda_{2}+\cdots+\lambda_{k}+\cdots+\lambda_{p}}. \]

Observación

• En conclusión, la medida cuantitativa de la información contenida en los componentes principales que realmente se utilizan se da por la relación de la suma de las varianzas de esos componentes principales a la suma de las varianzas de todos los componentes principales, lo que sirve como medida de la pérdida de información.

Example 7.1 (Relación entre estructura de correlación y pérdida de información)

Se analiza cómo la correlación entre variables afecta la varianza explicada por los componentes principales (PCA) en el caso bidimensional. Sean dos variables \(x_{1}\) y \(x_{2}\) con matriz de correlación muestral:

\[\begin{split} R = \begin{pmatrix} 1 & r \\ r & 1 \end{pmatrix}, \end{split}\]

donde \(r (>0)\) es el coeficiente de correlación muestral entre \(x_{1}\) y \(x_{2}\). La diagonal contiene correlaciones iguales a uno porque cada variable está perfectamente correlacionada consigo misma, y \(R\) es simétrica y positiva semidefinida.

Ecuación característica. Para obtener los autovalores, se resuelve:

\[\begin{split} |R - \lambda I_2| = \begin{vmatrix} 1-\lambda & r \\ r & 1-\lambda \end{vmatrix} = (1-\lambda)^2 - r^2 = \lambda^2 - 2\lambda + 1 - r^2 = 0. \end{split}\]

Las soluciones son

\[ \lambda_1 = 1 + r, \quad \lambda_2 = 1 - r. \]

• \(\lambda_1\) corresponde al primer componente principal (máxima varianza).

• \(\lambda_2\) corresponde al segundo componente (varianza residual).

• Cuando \(r \to 1\), se tiene \(\lambda_1 \to 2\) y \(\lambda_2 \to 0\), indicando que casi toda la varianza se concentra en un solo componente.

Autovectores. Para cada \(\lambda_i\), se resuelve \((R - \lambda_i I) \boldsymbol{w}_i = 0\). Las soluciones normalizadas son:

\[ \boldsymbol{w}_1 = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \ 1 \end{pmatrix}, \quad \boldsymbol{w}_2 = \frac{1}{\sqrt{2}} \begin{pmatrix} -1 \ 1 \end{pmatrix}. \]

• \(\boldsymbol{w}_1\) apunta en la dirección \(x_1 = x_2\) (ambas variables en conjunto).

• \(\boldsymbol{w}_2\) es perpendicular, representando diferencias entre ellas.

Componentes principales. Proyectando los datos sobre los autovectores:

\[ y_1 = \frac{1}{\sqrt{2}}x_1 + \frac{1}{\sqrt{2}}x_2, \quad y_2 = -\frac{1}{\sqrt{2}}x_1 + \frac{1}{\sqrt{2}}x_2. \]

• \(y_1\) captura la varianza compartida (información redundante).

• \(y_2\) recoge la varianza no redundante.

Proporción de varianza explicada. Las fracciones de varianza explicada por cada componente son:

\[ \frac{\lambda_1}{\lambda_1 + \lambda_2} = \frac{1+r}{2}, \quad \frac{\lambda_2}{\lambda_1 + \lambda_2} = \frac{1-r}{2}. \]

\(r\)	Var(\(y_1\))	Var(\(y_2\))
0.0	0.50	0.50
0.5	0.75	0.25
0.9	0.95	0.05

A medida que \(r\) aumenta:

• La varianza se concentra en el primer componente.

• El segundo componente pierde relevancia informativa.

• Por tanto, PCA puede reducir la dimensionalidad sin pérdida significativa cuando las variables están fuertemente correlacionadas.

• Como se muestra en la Figura Fig. 7.4, la contribución del primer componente principal, y, por lo tanto, la proporción que puede ser explicada únicamente por el primer componente principal, aumenta con la correlación creciente entre las dos variables.

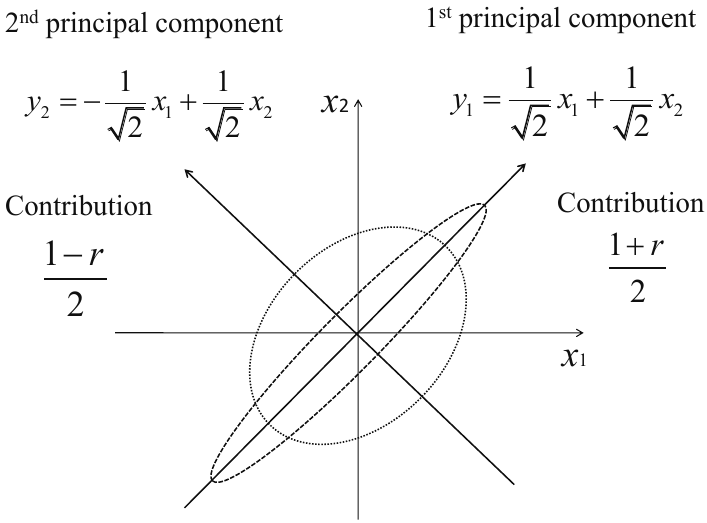
Fig. 7.4 Componentes principales basados en la matriz de correlación muestral y sus contribuciones. Fuente [Konishi, 2014].

7.8. Kernel PCA

El análisis de componentes principales (PCA) es un método eficaz para descubrir estructura en datos de alta dimensión mediante proyecciones sobre combinaciones lineales de las variables. Sin embargo, su alcance se limita a estructuras lineales. La pregunta que surge de manera natural es cómo detectar estructuras no lineales en datos dispersos en un espacio de alta dimensión. El PCA con kernels (kernel PCA) responde a esta pregunta combinando dos ideas:

• Reformular el problema de autovalores de la matriz de varianza-covarianza en términos de los productos internos entre observaciones.

• Reemplazar esos productos internos, calculados en un espacio de características de dimensión muy alta, por una función kernel que se evalúa directamente en el espacio de entrada (kernel trick).

Esta sección sigue ese orden. Los resultados se enuncian con precisión, pero las demostraciones se dejan como tareas guiadas, cada una con una estrategia sugerida y criterios de verificación (ver guía [Konishi, 2014]).

7.8.1. Centrado de los datos y problema de autovalores

Supongamos que se observan \(n\) datos \(p\)-dimensionales \(\boldsymbol{x}_1,\boldsymbol{x}_2,\dots,\boldsymbol{x}_n\). Se calcula el vector de medias muestral

\[ \bar{\boldsymbol{x}}=\frac{1}{n}\sum_{i=1}^{n}\boldsymbol{x}_i, \]

que corresponde al centroide de los datos, y se centran las observaciones: \(\boldsymbol{x}_i^{*}=\boldsymbol{x}_i-\bar{\boldsymbol{x}}\). El vector de medias de los datos centrados es

\[ \frac{1}{n}\sum_{i=1}^{n}\boldsymbol{x}_i^{*}=\frac{1}{n}\sum_{i=1}^{n}(\boldsymbol{x}_i-\bar{\boldsymbol{x}})=\boldsymbol{0}. \]

Con el centroide trasladado al origen se omite el asterisco y se escribe

(7.13)\[ \boldsymbol{x}_1,\boldsymbol{x}_2,\dots,\boldsymbol{x}_n;\qquad \sum_{i=1}^{n}\boldsymbol{x}_i=\boldsymbol{0}. \]

El PCA sobre los datos centrados consiste en hallar los autovalores y autovectores de la matriz de varianza-covarianza muestral

(7.14)\[ S=\frac{1}{n}\sum_{i=1}^{n}\boldsymbol{x}_i\boldsymbol{x}_i^{T}. \]

Observación sobre la normalización

En esta sección se usa el factor \(1/n\) en lugar de \(1/(n-1)\). Los autovectores no cambian, y los autovalores quedan multiplicados por el factor constante \((n-1)/n\). La elección con \(1/n\) simplifica las fórmulas del problema dual que se presenta a continuación.

Sean \(\lambda_1\ge\lambda_2\ge\cdots\ge\lambda_q>0\) los autovalores positivos de \(S\) y \(\boldsymbol{w}_1,\dots,\boldsymbol{w}_q\) los autovectores correspondientes, ortogonales entre sí y de norma uno:

(7.15)\[ S\boldsymbol{w}_\alpha=\lambda_\alpha\boldsymbol{w}_\alpha,\qquad \alpha=1,2,\dots,q. \]

La idea central consiste en reescribir el lado izquierdo de (7.15):

\[ S\boldsymbol{w}_\alpha=\frac{1}{n}\sum_{i=1}^{n}\boldsymbol{x}_i\boldsymbol{x}_i^{T}\boldsymbol{w}_\alpha=\frac{1}{n}\sum_{i=1}^{n}(\boldsymbol{x}_i^{T}\boldsymbol{w}_\alpha)\,\boldsymbol{x}_i=\lambda_\alpha\boldsymbol{w}_\alpha . \]

Si \(\lambda_\alpha\neq0\), el autovector \(\boldsymbol{w}_\alpha\) es una combinación lineal de los datos:

(7.16)\[ \boldsymbol{w}_\alpha=\sum_{i=1}^{n}c_{i\alpha}\boldsymbol{x}_i,\qquad c_{i\alpha}=\frac{1}{n\lambda_\alpha}\,\boldsymbol{x}_i^{T}\boldsymbol{w}_\alpha . \]

7.8.1.1. Forma matricial

Sea \(X\) la matriz de datos de orden \(n\times p\) cuyas filas son los datos centrados:

\[\begin{split} X=\begin{pmatrix}\boldsymbol{x}_1^{T}\\ \boldsymbol{x}_2^{T}\\ \vdots\\ \boldsymbol{x}_n^{T}\end{pmatrix},\qquad X^{T}=(\boldsymbol{x}_1,\boldsymbol{x}_2,\dots,\boldsymbol{x}_n). \end{split}\]

Entonces \(S=\frac{1}{n}X^{T}X\), y la relación (7.16) se escribe como \(\boldsymbol{w}_\alpha=X^{T}\boldsymbol{c}_\alpha\), donde \(\boldsymbol{c}_\alpha=(c_{1\alpha},\dots,c_{n\alpha})^{T}\). Se define además la matriz de Gram de los datos, de orden \(n\times n\):

(7.17)\[\begin{split} K=XX^{T}=\begin{pmatrix} \boldsymbol{x}_1^{T}\boldsymbol{x}_1 & \boldsymbol{x}_1^{T}\boldsymbol{x}_2 & \cdots & \boldsymbol{x}_1^{T}\boldsymbol{x}_n\\ \boldsymbol{x}_2^{T}\boldsymbol{x}_1 & \boldsymbol{x}_2^{T}\boldsymbol{x}_2 & \cdots & \boldsymbol{x}_2^{T}\boldsymbol{x}_n\\ \vdots & \vdots & \ddots & \vdots\\ \boldsymbol{x}_n^{T}\boldsymbol{x}_1 & \boldsymbol{x}_n^{T}\boldsymbol{x}_2 & \cdots & \boldsymbol{x}_n^{T}\boldsymbol{x}_n \end{pmatrix}. \end{split}\]

Proposición 1 (problema dual del PCA)

Sea \((\lambda,\boldsymbol{w})\) un par autovalor, autovector de \(S\) con \(\lambda>0\) y \(\|\boldsymbol{w}\|=1\). Entonces el vector \(\boldsymbol{c}=\frac{1}{n\lambda}X\boldsymbol{w}\) cumple:

• Inciso 1. \(\boldsymbol{w}=X^{T}\boldsymbol{c}\).

• Inciso 2. \(K\boldsymbol{c}=n\lambda\,\boldsymbol{c}\), es decir, \(\boldsymbol{c}\) es un autovector de \(K\) con autovalor \(n\lambda\).

• Inciso 3. \(n\lambda\,\boldsymbol{c}^{T}\boldsymbol{c}=1\).

Por consiguiente, el problema de autovalores de \(S\) (de orden \(p\)) se reemplaza por el problema de autovalores de \(K\) (de orden \(n\)):

(7.18)\[ K\boldsymbol{c}_\alpha=n\lambda_\alpha\boldsymbol{c}_\alpha,\qquad n\lambda_\alpha\,\boldsymbol{c}_\alpha^{T}\boldsymbol{c}_\alpha=1 . \]

Tarea 1: demostración de la Proposición 1

Enunciado. Demuestre los tres incisos de la Proposición 1.

Estrategia sugerida.

• Para el inciso 1, calcule \(X^{T}\boldsymbol{c}\) sustituyendo la definición de \(\boldsymbol{c}\) y reconozca la matriz \(S=\frac{1}{n}X^{T}X\). Use después que \(S\boldsymbol{w}=\lambda\boldsymbol{w}\).

• Para el inciso 2, escriba \(K\boldsymbol{c}=XX^{T}\boldsymbol{c}\) y aplique el inciso 1 para sustituir \(X^{T}\boldsymbol{c}\). Compare el resultado con la definición de \(\boldsymbol{c}\).

• Para el inciso 3, parta de \(1=\boldsymbol{w}^{T}\boldsymbol{w}\), sustituya \(\boldsymbol{w}=X^{T}\boldsymbol{c}\) e identifique la forma cuadrática \(\boldsymbol{c}^{T}K\boldsymbol{c}\). Luego use el inciso 2.

Pista. La derivación habitual parte de \(\frac{1}{n}X^{T}XX^{T}\boldsymbol{c}=\lambda X^{T}\boldsymbol{c}\), multiplica por la izquierda por \(X\) y obtiene \(K^{2}\boldsymbol{c}=n\lambda K\boldsymbol{c}\). De esta igualdad no se puede concluir directamente \(K\boldsymbol{c}=n\lambda\boldsymbol{c}\), porque \(K\) puede ser singular y, por tanto, no se puede cancelar un factor \(K\). Explique con sus propias palabras por qué la ruta sugerida en los pasos anteriores, que construye \(\boldsymbol{c}\) explícitamente, evita esta dificultad.

Verificación. Compruebe las dimensiones de cada producto matricial. Compruebe también que, si \(\boldsymbol{w}\) tiene norma uno, la constante \(\frac{1}{n\lambda}\) es exactamente la que hace que \(\boldsymbol{c}\) cumpla el inciso 3.

Proposición 2 (recíproca y puntuaciones)

• Inciso 1. Si \((\mu,\boldsymbol{c})\) es un par autovalor, autovector de \(K\) con \(\mu>0\) y \(\mu\,\boldsymbol{c}^{T}\boldsymbol{c}=1\), entonces \(\boldsymbol{w}=X^{T}\boldsymbol{c}\) es un autovector de \(S\) de norma uno con autovalor \(\mu/n\).

• Inciso 2. Los autovalores no nulos de \(S\) y de \(K/n\) coinciden, con las mismas multiplicidades.

• Inciso 3. La \(\alpha\)-ésima componente principal de una observación \(\boldsymbol{x}\) es

  (7.19)\[ y_\alpha=\boldsymbol{w}_\alpha^{T}\boldsymbol{x}=\sum_{i=1}^{n}c_{i\alpha}\,\boldsymbol{x}_i^{T}\boldsymbol{x}. \]

Tarea 2: demostración de la Proposición 2

Enunciado. Demuestre los tres incisos de la Proposición 2.

Estrategia sugerida.

• Para el inciso 1, calcule \(S\boldsymbol{w}=\frac{1}{n}X^{T}XX^{T}\boldsymbol{c}=\frac{1}{n}X^{T}K\boldsymbol{c}\) y use que \(\boldsymbol{c}\) es autovector de \(K\). Para la norma, repita el cálculo \(\boldsymbol{w}^{T}\boldsymbol{w}=\boldsymbol{c}^{T}K\boldsymbol{c}\). Justifique además que \(\boldsymbol{w}\neq\boldsymbol{0}\).

• Para el inciso 2, use la Proposición 1 y el inciso 1 de esta proposición para construir una correspondencia entre autovectores de \(S\) y de \(K\). Demuestre que dos autovectores ortogonales de \(K\) asociados al mismo autovalor producen autovectores ortogonales de \(S\), lo que preserva las multiplicidades.

• Para el inciso 3, aplique \(\boldsymbol{w}_\alpha=X^{T}\boldsymbol{c}_\alpha\) a \(\boldsymbol{w}_\alpha^{T}\boldsymbol{x}\) y use la linealidad del producto interno.

Pista. Existe una ruta alternativa para el inciso 2: los productos \(AB\) y \(BA\) tienen los mismos autovalores no nulos. Identifique \(A\) y \(B\) tales que \(AB=S\) y \(BA=K/n\), y demuestre el resultado general de que \(AB\) y \(BA\) comparten su espectro no nulo.

Verificación. Calcule, para una muestra pequeña con \(n=3\) y \(p=2\) elegida por usted, los autovalores de \(S\) y de \(K/n\) y compruebe que los no nulos coinciden. Observe también que \(K\) tiene \(n\) autovalores, de los cuales a lo sumo \(\min(n,p)\) pueden ser no nulos.

7.8.2. Aplicación a datos transformados a un RKHS

La linealidad del PCA limita su capacidad cuando la estructura de los datos es no lineal. De manera análoga a lo que ocurre en las máquinas de vectores de soporte, se transforman los datos a un espacio de dimensión mayor, denominado espacio de características, donde sí se aplica el PCA lineal. Sea

(7.20)\[ \Phi(\boldsymbol{x})=(\phi_1(\boldsymbol{x}),\phi_2(\boldsymbol{x}),\dots,\phi_r(\boldsymbol{x}))^{T} \]

una función no lineal de \(\mathbb{R}^p\) en \(\mathbb{R}^r\), con \(r>p\) y componentes \(\phi_j\) de valor real. Los datos transformados son \(\Phi(\boldsymbol{x}_1),\dots,\Phi(\boldsymbol{x}_n)\). Primero se centran en el espacio de características:

(7.21)\[ \bar{\Phi}=\frac{1}{n}\sum_{i=1}^{n}\Phi(\boldsymbol{x}_i),\qquad \Phi_c(\boldsymbol{x}_i)=\Phi(\boldsymbol{x}_i)-\bar{\Phi},\qquad \sum_{i=1}^{n}\Phi_c(\boldsymbol{x}_i)=\boldsymbol{0}. \]

Sea \(Z_c=(\Phi_c(\boldsymbol{x}_1),\dots,\Phi_c(\boldsymbol{x}_n))^{T}\) la matriz de orden \(n\times r\) con los datos centrados como filas. La matriz de varianza-covarianza en el espacio de características y su matriz de Gram son

(7.22)\[ S_c=\frac{1}{n}\sum_{i=1}^{n}\Phi_c(\boldsymbol{x}_i)\Phi_c(\boldsymbol{x}_i)^{T}=\frac{1}{n}Z_c^{T}Z_c,\qquad K_c=Z_cZ_c^{T}, \]

donde \((K_c)_{jk}=\Phi_c(\boldsymbol{x}_j)^{T}\Phi_c(\boldsymbol{x}_k)\).

Proposición 3 (PCA en el espacio de características)

Sea \((\lambda_\alpha^{F},\boldsymbol{w}_\alpha^{F})\) un par autovalor, autovector de \(S_c\) con \(\lambda_\alpha^{F}>0\) y \(\|\boldsymbol{w}_\alpha^{F}\|=1\). Entonces:

• Inciso 1. \(\boldsymbol{w}_\alpha^{F}=Z_c^{T}\boldsymbol{c}_\alpha^{F}=\sum_{i=1}^{n}c_{i\alpha}^{F}\,\Phi_c(\boldsymbol{x}_i)\), donde \(\boldsymbol{c}_\alpha^{F}\) satisface

  (7.23)\[ K_c\,\boldsymbol{c}_\alpha^{F}=n\lambda_\alpha^{F}\,\boldsymbol{c}_\alpha^{F},\qquad n\lambda_\alpha^{F}\,(\boldsymbol{c}_\alpha^{F})^{T}\boldsymbol{c}_\alpha^{F}=1 . \]

• Inciso 2. La \(\alpha\)-ésima componente principal de una observación \(\boldsymbol{x}\) es

  (7.24)\[ y_\alpha^{F}=(\boldsymbol{w}_\alpha^{F})^{T}\Phi_c(\boldsymbol{x})=\sum_{i=1}^{n}c_{i\alpha}^{F}\,\Phi_c(\boldsymbol{x}_i)^{T}\Phi_c(\boldsymbol{x}). \]

• Inciso 3. \(K_c\boldsymbol{1}_n=\boldsymbol{0}\). En consecuencia, \(\operatorname{rank}(K_c)\le n-1\) y existen a lo sumo \(n-1\) componentes principales con autovalor no nulo.

Tarea 3: demostración de la Proposición 3

Enunciado. Demuestre los tres incisos de la Proposición 3.

Estrategia sugerida.

• Para los incisos 1 y 2, no repita los cálculos desde cero. Identifique qué propiedades de \(X\) se utilizaron en las Tareas 1 y 2. Observará que solo se emplearon identidades matriciales de la forma \(S=\frac{1}{n}X^{T}X\) y \(K=XX^{T}\). Concluya que las demostraciones son válidas al reemplazar \(X\) por \(Z_c\), y escriba explícitamente la sustitución en cada paso.

• Para el inciso 3, calcule \(Z_c^{T}\boldsymbol{1}_n\) y use la condición de centrado (7.21). Luego escriba \(K_c\boldsymbol{1}_n=Z_c(Z_c^{T}\boldsymbol{1}_n)\).

• Para la consecuencia sobre el rango, relacione \(K_c\boldsymbol{1}_n=\boldsymbol{0}\) con el kernel (espacio nulo) de \(K_c\).

Pista. La dimensión \(r\) puede ser muy grande e incluso infinita (como ocurre con el kernel gaussiano). Discuta brevemente por qué esto no afecta el argumento: toda la información necesaria está contenida en la matriz \(K_c\) de orden \(n\times n\), que siempre tiene dimensión finita.

Verificación. Compruebe numéricamente, en una muestra pequeña y con una \(\Phi\) explícita de su elección, que \(K_c\boldsymbol{1}_n\) es el vector nulo salvo errores de redondeo.

7.8.3. Funciones kernel

Calcular directamente los productos internos \(\Phi_c(\boldsymbol{x}_j)^{T}\Phi_c(\boldsymbol{x}_k)\) puede resultar inviable cuando \(r\) es muy grande. El kernel trick evita esta dificultad: se elige una función \(K(\boldsymbol{x},\boldsymbol{y})\) que se evalúa en el espacio de entrada y que cumple

(7.25)\[ K(\boldsymbol{x}_j,\boldsymbol{x}_k)=\Phi(\boldsymbol{x}_j)^{T}\Phi(\boldsymbol{x}_k). \]

De este modo, el valor del producto interno en el espacio de características se obtiene como un valor calculable de la función kernel, sin necesidad de conocer \(\Phi\). Dos ejemplos representativos son:

\[ K(\boldsymbol{x},\boldsymbol{y})=\bigl(\boldsymbol{x}^{T}\boldsymbol{y}+1\bigr)^{d}\quad\text{(kernel polinomial de grado } d\text{)}, \]

(7.26)\[ K(\boldsymbol{x},\boldsymbol{y})=\exp\!\left\{-\frac{\|\boldsymbol{x}-\boldsymbol{y}\|^{2}}{2\sigma^{2}}\right\}\quad\text{(kernel gaussiano, con } \sigma>0\text{)}. \]

Ambos se calculan a partir de operaciones en el espacio de entrada de dimensión \(p\). Con un kernel \(K\), los datos se presentan como componentes principales no lineales en el espacio de entrada, ya que la componente \(y_\alpha=\sum_{i}c_{i\alpha}K_c(\boldsymbol{x}_i,\boldsymbol{x})\) es una función no lineal de \(\boldsymbol{x}\), aunque sea lineal en el espacio de características. Por ejemplo, con el kernel polinomial,

\[ y_\alpha=\sum_{i=1}^{n}c_{i\alpha}\bigl(\boldsymbol{x}_i^{T}\boldsymbol{x}+1\bigr)^{d}\quad\text{(salvo el centrado)}. \]

Proposición 4 (matriz de Gram de un kernel)

Sea \(K(\boldsymbol{x},\boldsymbol{y})=\Phi(\boldsymbol{x})^{T}\Phi(\boldsymbol{y})\) y sean \(\boldsymbol{x}_1,\dots,\boldsymbol{x}_n\) puntos cualesquiera. La matriz \(\mathbf{K}\) de elementos \(\mathbf{K}_{jk}=K(\boldsymbol{x}_j,\boldsymbol{x}_k)\) es simétrica y semidefinida positiva.

Recíprocamente (teorema de Mercer y de Moore-Aronszajn, que se enuncia sin demostración), toda función simétrica cuyas matrices de Gram sean siempre semidefinidas positivas puede escribirse como un producto interno en algún espacio de características. Esta es la condición práctica para decidir si una función es un kernel válido.

Tarea 4: demostración de la Proposición 4

Enunciado. Demuestre que \(\mathbf{K}\) es simétrica y semidefinida positiva.

Estrategia sugerida.

• La simetría se deduce de la simetría del producto interno euclídeo.

• Para la semidefinición positiva, tome un vector arbitrario \(\boldsymbol{a}\in\mathbb{R}^{n}\) y desarrolle \(\boldsymbol{a}^{T}\mathbf{K}\boldsymbol{a}=\sum_{j,k}a_ja_k\Phi(\boldsymbol{x}_j)^{T}\Phi(\boldsymbol{x}_k)\).

• Agrupe la doble suma para reconocer el cuadrado de la norma de un vector del espacio de características.

Pista. Defina \(\boldsymbol{v}=\sum_{j=1}^{n}a_j\Phi(\boldsymbol{x}_j)\) y calcule \(\|\boldsymbol{v}\|^{2}\).

Verificación. La conclusión debe ser \(\boldsymbol{a}^{T}\mathbf{K}\boldsymbol{a}=\|\boldsymbol{v}\|^{2}\ge0\) para todo \(\boldsymbol{a}\). Explique por qué esto equivale a que todos los autovalores de \(\mathbf{K}\) sean no negativos.

Tarea 5: representación explícita del kernel polinomial

Enunciado. Sea \(p=2\) y \(d=2\). Encuentre una función \(\Phi:\mathbb{R}^{2}\to\mathbb{R}^{6}\) tal que \(\Phi(\boldsymbol{x})^{T}\Phi(\boldsymbol{y})=(\boldsymbol{x}^{T}\boldsymbol{y}+1)^{2}\) para todo \(\boldsymbol{x},\boldsymbol{y}\in\mathbb{R}^{2}\).

Estrategia sugerida.

• Escriba \(\boldsymbol{x}=(x_1,x_2)^{T}\), \(\boldsymbol{y}=(y_1,y_2)^{T}\) y desarrolle \((1+x_1y_1+x_2y_2)^{2}\) mediante el cuadrado de un trinomio.

• Agrupe los seis términos resultantes de modo que cada uno tenga la forma (función de \(\boldsymbol{x}\)) por (la misma función de \(\boldsymbol{y}\)).

• Lea las seis funciones de \(\boldsymbol{x}\) y colóquelas como componentes de \(\Phi(\boldsymbol{x})\).

Pista. Los términos cruzados aparecen con coeficiente 2. Para repartirlos de forma simétrica entre \(\Phi(\boldsymbol{x})\) y \(\Phi(\boldsymbol{y})\) necesitará factores del tipo \(\sqrt{2}\).

Verificación. Elija dos puntos concretos, por ejemplo \(\boldsymbol{x}=(1,2)^{T}\) y \(\boldsymbol{y}=(3,-1)^{T}\), y compruebe numéricamente que ambos lados de la igualdad coinciden. Discuta además qué ocurre con la dimensión \(r\) de \(\Phi\) cuando \(p\) y \(d\) crecen, y por qué esto motiva el uso del kernel.

Tarea 6: el kernel gaussiano es semidefinido positivo

Enunciado. Demuestre que, para cualesquiera puntos \(\boldsymbol{x}_1,\dots,\boldsymbol{x}_n\) y \(\sigma>0\), la matriz \(\mathbf{K}_{jk}=\exp\{-\|\boldsymbol{x}_j-\boldsymbol{x}_k\|^{2}/(2\sigma^{2})\}\) es semidefinida positiva.

Estrategia sugerida.

• Desarrolle \(\|\boldsymbol{x}-\boldsymbol{y}\|^{2}=\|\boldsymbol{x}\|^{2}+\|\boldsymbol{y}\|^{2}-2\boldsymbol{x}^{T}\boldsymbol{y}\) y factorice el kernel en tres factores: \(e^{-\|\boldsymbol{x}\|^{2}/2\sigma^{2}}\), \(e^{-\|\boldsymbol{y}\|^{2}/2\sigma^{2}}\) y \(e^{\boldsymbol{x}^{T}\boldsymbol{y}/\sigma^{2}}\).

• Demuestre que si \(\mathbf{K}\) es semidefinida positiva y \(g\) es una función real, entonces la matriz de elementos \(g(\boldsymbol{x}_j)\mathbf{K}_{jk}g(\boldsymbol{x}_k)\) también lo es (es una congruencia \(D\mathbf{K}D\) con \(D\) diagonal).

• Desarrolle \(e^{t}=\sum_{m\ge0}t^{m}/m!\) con \(t=\boldsymbol{x}^{T}\boldsymbol{y}/\sigma^{2}\). Cada sumando es una potencia de un kernel lineal.

• Use el teorema del producto de Schur (el producto elemento a elemento de dos matrices semidefinidas positivas es semidefinido positivo), que debe demostrar o citar con precisión, para concluir que cada potencia es semidefinida positiva. Termine usando que sumas con coeficientes positivos y límites de matrices semidefinidas positivas son semidefinidas positivas.

Pista. Para el teorema de Schur, escriba \(A=\sum_{k}\mu_k\boldsymbol{u}_k\boldsymbol{u}_k^{T}\) con \(\mu_k\ge0\) y observe que \(A\circ B=\sum_{k}\mu_k\,D_{\boldsymbol{u}_k}BD_{\boldsymbol{u}_k}\), donde \(D_{\boldsymbol{u}}=\operatorname{diag}(\boldsymbol{u})\).

Verificación. Compruebe numéricamente, con una muestra aleatoria y distintos valores de \(\sigma\), que el menor autovalor de \(\mathbf{K}\) es no negativo salvo errores de redondeo.

7.8.4. Justificación del centrado de los datos

Hasta aquí el centrado se ha presentado como un paso preliminar, casi mecánico. Sin embargo, no es un convenio de notación ni una simplificación cosmética: es una condición que determina qué objeto estadístico se está diagonalizando. En esta subsección se justifica la necesidad de centrar desde cinco perspectivas complementarias:

• Estadística. Sin centrado se diagonaliza la matriz de segundos momentos y no la de covarianzas.

• Variacional y geométrica. El subespacio óptimo de aproximación es afín y pasa por el centroide.

• Interpretativa. Las nociones de varianza explicada y de componentes incorrelacionadas dependen del centrado.

• Algebraica. El problema dual y la estructura de la matriz de Gram requieren datos centrados.

• Específica del espacio de características. El centrado en el espacio de entrada no se hereda a \(\Phi(\boldsymbol{x})\), y omitirlo en ese espacio degenera el método.

7.8.5. Centrado de los datos mediante la función núcleo

Queda pendiente un problema práctico: el vector de medias \(\bar{\Phi}\) de (7.21) no puede calcularse porque \(\Phi\) no se conoce explícitamente. La solución consiste en expresar \(K_c\) en términos del núcleo no centrado \(K(\boldsymbol{x}_j,\boldsymbol{x}_k)=\Phi(\boldsymbol{x}_j)^{T}\Phi(\boldsymbol{x}_k)\).

Proposición 5 (centrado mediante el núcleo)

Sea \(\mathbf{K}\) la matriz de orden \(n\) con elementos \(K(\boldsymbol{x}_j,\boldsymbol{x}_k)\) y sea \(H=I_n-\frac{1}{n}\boldsymbol{1}_n\boldsymbol{1}_n^{T}\) la matriz de centrado. Entonces:

• Inciso 1. Elemento a elemento,

  (7.27)\[ K_c(\boldsymbol{x}_j,\boldsymbol{x}_k)=K(\boldsymbol{x}_j,\boldsymbol{x}_k)-\frac{1}{n}\sum_{r=1}^{n}K(\boldsymbol{x}_r,\boldsymbol{x}_k)-\frac{1}{n}\sum_{s=1}^{n}K(\boldsymbol{x}_j,\boldsymbol{x}_s)+\frac{1}{n^{2}}\sum_{r=1}^{n}\sum_{s=1}^{n}K(\boldsymbol{x}_r,\boldsymbol{x}_s). \]

• Inciso 2. En forma matricial,

  (7.28)\[ K_c=H\,\mathbf{K}\,H=\Bigl(I_n-\tfrac{1}{n}\boldsymbol{1}_n\boldsymbol{1}_n^{T}\Bigr)\mathbf{K}\Bigl(I_n-\tfrac{1}{n}\boldsymbol{1}_n\boldsymbol{1}_n^{T}\Bigr). \]

• Inciso 3. Para una observación nueva \(\boldsymbol{x}\), el núcleo centrado respecto de los datos de entrenamiento es

  (7.29)\[ K_c(\boldsymbol{x}_i,\boldsymbol{x})=K(\boldsymbol{x}_i,\boldsymbol{x})-\frac{1}{n}\sum_{r=1}^{n}K(\boldsymbol{x}_r,\boldsymbol{x})-\frac{1}{n}\sum_{s=1}^{n}K(\boldsymbol{x}_i,\boldsymbol{x}_s)+\frac{1}{n^{2}}\sum_{r=1}^{n}\sum_{s=1}^{n}K(\boldsymbol{x}_r,\boldsymbol{x}_s). \]

Tarea 7: centrado elemento a elemento

Enunciado. Demuestre los incisos 1 y 3 de la Proposición 5.

Estrategia sugerida.

• Escriba \(\Phi_c(\boldsymbol{x}_j)^{T}\Phi_c(\boldsymbol{x}_k)=\bigl(\Phi(\boldsymbol{x}_j)-\frac{1}{n}\sum_r\Phi(\boldsymbol{x}_r)\bigr)^{T}\bigl(\Phi(\boldsymbol{x}_k)-\frac{1}{n}\sum_s\Phi(\boldsymbol{x}_s)\bigr)\).

• Desarrolle el producto en cuatro términos, usando la bilinealidad del producto interno.

• Reconozca en cada término un valor de \(K\) mediante (7.25). Preste atención a que las sumas dobles \(\sum_r\sum_s\) aparecen con el coeficiente \(1/n^{2}\).

• Para el inciso 3, repita el procedimiento con \(\Phi_c(\boldsymbol{x})=\Phi(\boldsymbol{x})-\bar{\Phi}\), donde la media \(\bar{\Phi}\) se sigue calculando con los \(n\) datos de entrenamiento.

Pista. Los dos términos intermedios son simétricos entre sí cuando \(\boldsymbol{x}_j\) y \(\boldsymbol{x}_k\) se intercambian, pero no son iguales en general para una observación nueva \(\boldsymbol{x}\). Verifique con cuidado qué índice recorre cada suma.

Verificación. Compruebe que el inciso 3 coincide con el inciso 1 cuando \(\boldsymbol{x}\) es uno de los datos de entrenamiento. Compruebe también, con un ejemplo numérico pequeño, que la matriz resultante tiene filas y columnas que suman cero.

Tarea 8: centrado matricial

Enunciado. Demuestre el inciso 2 de la Proposición 5 y verifique su equivalencia con el inciso 1.

Estrategia sugerida.

• Demuestre que \(H\) es simétrica, idempotente (\(H^{2}=H\)) y satisface \(H\boldsymbol{1}_n=\boldsymbol{0}\).

• Demuestre que \(Z_c=HZ\), donde \(Z=(\Phi(\boldsymbol{x}_1),\dots,\Phi(\boldsymbol{x}_n))^{T}\). Para ello exprese el vector de medias como \(\bar{\Phi}=\frac{1}{n}Z^{T}\boldsymbol{1}_n\) y la matriz de medias replicadas como \(\frac{1}{n}\boldsymbol{1}_n\boldsymbol{1}_n^{T}Z\).

• Calcule \(K_c=Z_cZ_c^{T}=HZZ^{T}H^{T}\) y reconozca \(\mathbf{K}=ZZ^{T}\).

• Para la equivalencia con el inciso 1, calcule el elemento \((j,k)\) de \(H\mathbf{K}H\) en dos pasos. Primero obtenga \((H\mathbf{K})_{jk}\), que resta a cada columna su media. Luego multiplique por \(H\) a la derecha, que resta a cada fila su media.

Pista. Interprete geométricamente \(H\): el producto \(H\boldsymbol{v}\) resta a \(\boldsymbol{v}\) la media de sus componentes, es decir, proyecta ortogonalmente sobre el complemento de \(\boldsymbol{1}_n\). Esto explica de forma natural las propiedades del primer paso.

Verificación. Compruebe numéricamente que \(\boldsymbol{1}_n^{T}K_c=\boldsymbol{0}^{T}\) y que \(K_c\boldsymbol{1}_n=\boldsymbol{0}\), lo cual es coherente con el inciso 3 de la Proposición 3.

Tarea 9: forma vectorial para una observación nueva

Enunciado. Sea \(\boldsymbol{k}(\boldsymbol{x})=(K(\boldsymbol{x}_1,\boldsymbol{x}),\dots,K(\boldsymbol{x}_n,\boldsymbol{x}))^{T}\). Demuestre que el vector \(\boldsymbol{k}_c(\boldsymbol{x})\) cuyas componentes son los \(K_c(\boldsymbol{x}_i,\boldsymbol{x})\) de (7.29) puede escribirse como

\[ \boldsymbol{k}_c(\boldsymbol{x})=\boldsymbol{k}(\boldsymbol{x})-\frac{1}{n}\bigl(\boldsymbol{1}_n^{T}\boldsymbol{k}(\boldsymbol{x})\bigr)\boldsymbol{1}_n-\frac{1}{n}\mathbf{K}\boldsymbol{1}_n+\frac{1}{n^{2}}\bigl(\boldsymbol{1}_n^{T}\mathbf{K}\boldsymbol{1}_n\bigr)\boldsymbol{1}_n . \]

Concluya que las puntuaciones de \(\boldsymbol{x}\) sobre las primeras \(m\) componentes son las componentes del vector \(C^{T}\boldsymbol{k}_c(\boldsymbol{x})\), con \(C=(\boldsymbol{c}_1^{F},\dots,\boldsymbol{c}_m^{F})\).

Estrategia sugerida.

• Interprete cada término de (7.29) como la \(i\)-ésima componente de un vector de \(\mathbb{R}^{n}\). Identifique, por ejemplo, que \(\frac{1}{n}\sum_s K(\boldsymbol{x}_i,\boldsymbol{x}_s)\) es la \(i\)-ésima componente de \(\frac{1}{n}\mathbf{K}\boldsymbol{1}_n\).

• Identifique el escalar \(\frac{1}{n^{2}}\sum_r\sum_s K(\boldsymbol{x}_r,\boldsymbol{x}_s)\) con \(\frac{1}{n^{2}}\boldsymbol{1}_n^{T}\mathbf{K}\boldsymbol{1}_n\).

• Use (7.24) para expresar \(y_\alpha^{F}=(\boldsymbol{c}_\alpha^{F})^{T}\boldsymbol{k}_c(\boldsymbol{x})\) y apile los \(m\) resultados.

Verificación. Compruebe que, si \(\boldsymbol{x}=\boldsymbol{x}_j\) es un dato de entrenamiento, entonces \(\boldsymbol{k}_c(\boldsymbol{x}_j)\) es la \(j\)-ésima columna de \(K_c\), y que las puntuaciones de entrenamiento resultan ser \(K_cC\).

7.8.6. Algoritmo del PCA con núcleos

Los resultados anteriores se resumen en el siguiente procedimiento. Dados \(n\) datos \(\boldsymbol{x}_1,\dots,\boldsymbol{x}_n\) de dimensión \(p\):

• Paso 1, elegir un núcleo. Seleccione una función núcleo \(K\) (por ejemplo, la gaussiana con un valor de \(\sigma\)) y construya la matriz \(\mathbf{K}\) de orden \(n\) con elementos \(K(\boldsymbol{x}_j,\boldsymbol{x}_k)\).

• Paso 2, centrar. Calcule \(K_c=H\mathbf{K}H\) según (7.28).

• Paso 3, resolver el problema de autovalores. Obtenga los autovalores y autovectores de \(K_c\):

  (7.30)\[ K_c\,\boldsymbol{c}^{F}=n\lambda^{F}\,\boldsymbol{c}^{F},\qquad n\lambda^{F}\,(\boldsymbol{c}^{F})^{T}\boldsymbol{c}^{F}=1 . \]

• Paso 4, ordenar y normalizar. Ordene los autovalores de mayor a menor. Si \(\mu_\alpha\) es el \(\alpha\)-ésimo autovalor de \(K_c\) con autovector unitario \(\boldsymbol{v}_\alpha\), entonces \(n\lambda_\alpha^{F}=\mu_\alpha\) y el vector de coeficientes es \(\boldsymbol{c}_\alpha^{F}=\boldsymbol{v}_\alpha/\sqrt{\mu_\alpha}\).

• Paso 5, proyectar. La \(\alpha\)-ésima componente principal de una observación \(\boldsymbol{x}\) es

  (7.31)\[ y_\alpha=\sum_{i=1}^{n}c_{i\alpha}^{F}\,K_c(\boldsymbol{x}_i,\boldsymbol{x}), \]

  donde \(K_c(\boldsymbol{x}_i,\boldsymbol{x})\) se calcula con (7.29).

Consideraciones prácticas

Costo computacional. El método requiere almacenar \(\mathbf{K}\) (\(n^{2}\) elementos) y diagonalizarla (del orden de \(n^{3}\) operaciones). Por ello es ventajoso cuando \(p\) es grande y \(n\) moderado, y costoso cuando \(n\) es muy grande. En ese caso se recurre a aproximaciones como el método de Nyström o las características aleatorias de Fourier.

Hiperparámetros. Los resultados dependen de la elección del núcleo y de sus parámetros. Con el núcleo gaussiano, un valor muy pequeño de \(\sigma\) hace que \(\mathbf{K}\) se aproxime a la identidad (cada punto solo se parece a sí mismo), mientras que un valor muy grande la aproxima a una matriz constante (todos los puntos se parecen).

Interpretación. A diferencia del PCA lineal, los autovectores \(\boldsymbol{w}_\alpha^{F}\) viven en el espacio de características y, en general, no tienen una representación explícita en el espacio de entrada. Por esta razón, reconstruir un punto del espacio de entrada a partir de sus puntuaciones (problema de la preimagen) es un problema difícil que no se aborda en esta sección.

7.8.7. Implementación en Python

El siguiente código implementa el algoritmo anterior desde cero con NumPy y lo contrasta con la implementación de scikit-learn sobre dos circunferencias concéntricas, un conjunto de datos que ninguna proyección lineal puede separar.

import numpy as np                                      # Álgebra lineal y arreglos numéricos
import matplotlib.pyplot as plt                         # Gráficos
from sklearn.datasets import make_circles               # Generador de dos circunferencias concéntricas
from sklearn.decomposition import PCA, KernelPCA        # PCA lineal y PCA con kernel de scikit-learn


# Tamaños de letra grandes para que todo se lea bien dentro del libro
plt.rcParams.update({
    "font.size": 14,                                    # Tamaño base del texto
    "axes.titlesize": 16,                               # Tamaño de los títulos de cada panel
    "axes.labelsize": 14,                               # Tamaño de los nombres de los ejes
    "xtick.labelsize": 12,                              # Tamaño de los números del eje horizontal
    "ytick.labelsize": 12,                              # Tamaño de los números del eje vertical
    "legend.fontsize": 12,                              # Tamaño del texto de la leyenda
})


def gaussian_kernel_matrix(A, B, sigma):
    """Matriz de kernel gaussiano entre las filas de A (m x p) y las filas de B (n x p)."""
    sq_dist = (
        np.sum(A**2, axis=1)[:, None]                   # Norma al cuadrado de cada fila de A (columna)
        + np.sum(B**2, axis=1)[None, :]                 # Norma al cuadrado de cada fila de B (fila)
        - 2.0 * A @ B.T                                 # Menos el doble del producto interno
    )                                                   # Resultado: distancias euclídeas al cuadrado
    return np.exp(-np.maximum(sq_dist, 0.0) / (2.0 * sigma**2))  # Kernel gaussiano (se evitan negativos por redondeo)


def kernel_pca_fit(X, sigma, n_components):
    """Ajusta el PCA con kernel gaussiano siguiendo los pasos 1 a 4 del algoritmo."""
    n = X.shape[0]                                      # Número de observaciones
    K = gaussian_kernel_matrix(X, X, sigma)             # Paso 1: matriz del kernel
    H = np.eye(n) - np.ones((n, n)) / n                 # Matriz de centrado
    Kc = H @ K @ H                                      # Paso 2: matriz del kernel centrada
    mu, V = np.linalg.eigh(Kc)                          # Paso 3: autovalores y autovectores (mu = n * lambda)
    order = np.argsort(mu)[::-1][:n_components]         # Paso 4: índices de los mayores autovalores
    mu, V = mu[order], V[:, order]                      # Se conservan los autovalores y autovectores elegidos
    C = V / np.sqrt(mu)                                 # Normalización n*lambda*c'c = 1
    return {"X": X, "K": K, "Kc": Kc, "C": C, "mu": mu, "sigma": sigma}  # Se guarda todo lo necesario para proyectar


def kernel_pca_transform(model, X_new):
    """Calcula las puntuaciones de observaciones nuevas (paso 5), usando el kernel centrado."""
    K, C, sigma = model["K"], model["C"], model["sigma"]             # Se recuperan los objetos del modelo
    k = gaussian_kernel_matrix(X_new, model["X"], sigma)             # Kernel entre datos nuevos y de entrenamiento (m x n)
    k_c = (
        k                                                            # Kernel sin centrar
        - k.mean(axis=1, keepdims=True)                              # Resta el promedio de cada fila de k
        - K.mean(axis=0, keepdims=True)                              # Resta el promedio de columnas de K de entrenamiento
        + K.mean()                                                   # Suma el promedio global de K de entrenamiento
    )
    return k_c @ C                                                   # Puntuaciones: kernel centrado por coeficientes


# Datos: dos circunferencias concéntricas
X, labels = make_circles(n_samples=300, factor=0.3, noise=0.05, random_state=0)  # Etiqueta 0 = externa, 1 = interna

sigma = 0.3                                                          # Ancho del kernel gaussiano
model = kernel_pca_fit(X, sigma=sigma, n_components=2)               # Se ajusta el PCA con kernel
Y_kpca = kernel_pca_transform(model, X)                              # Puntuaciones del PCA con kernel
Y_pca = PCA(n_components=2).fit_transform(X)                         # Puntuaciones del PCA lineal

# Comprobación 1: las puntuaciones de entrenamiento coinciden con Kc @ C
assert np.allclose(Y_kpca, model["Kc"] @ model["C"], atol=1e-8)

# Comprobación 2: los autovalores coinciden con los de scikit-learn
skl = KernelPCA(n_components=2, kernel="rbf", gamma=1.0 / (2.0 * sigma**2)).fit(X)
assert np.allclose(model["mu"], skl.eigenvalues_, rtol=1e-6)

# Colores y nombres de cada clase (se fijan a mano para poder crear una leyenda clara)
classes = [
    (0, "Outer circle", "#3B4CC0"),                     # Clase 0: círculo externo, azul
    (1, "Inner circle", "#B40426"),                     # Clase 1: círculo interno, rojo
]

# Figura 2 x 2: cada panel es más grande que en la versión de una sola fila
fig, axes = plt.subplots(2, 2, figsize=(12, 10), dpi=150)  # Tamaño grande y alta resolución
ax_orig, ax_pca, ax_kpca, ax_hist = axes.ravel()           # Se asigna un nombre a cada panel

# Paneles de dispersión: se dibuja cada clase por separado para generar la leyenda
panels = [
    (ax_orig, X, "Original data", "$x_1$", "$x_2$"),                                   # Datos originales
    (ax_pca, Y_pca, "Linear PCA", "Component 1", "Component 2"),                      # PCA lineal
    (ax_kpca, Y_kpca, r"Gaussian kernel PCA ($\sigma=0.3$)", "Component 1", "Component 2"),  # PCA con kernel
]
for ax, data, title, xlabel, ylabel in panels:                                         # Se recorre cada panel
    for value, name, color in classes:                                                 # Se recorre cada clase
        mask = labels == value                                                         # Selecciona los puntos de la clase
        ax.scatter(data[mask, 0], data[mask, 1], c=color, s=35,
                   edgecolor="white", linewidth=0.4, label=name)                       # Puntos grandes con borde blanco
    ax.set_title(title)                                                                # Título del panel
    ax.set_xlabel(xlabel)                                                              # Nombre del eje horizontal
    ax.set_ylabel(ylabel)                                                              # Nombre del eje vertical
    ax.grid(alpha=0.3)                                                                 # Cuadrícula suave
    ax.legend(loc="best", frameon=True)                                                # Leyenda con las dos clases

# Los dos primeros paneles comparten escala en ambos ejes para no deformar los círculos
ax_orig.set_aspect("equal", adjustable="datalim")       # Escala igual en el panel de datos originales
ax_pca.set_aspect("equal", adjustable="datalim")        # Escala igual en el panel de PCA lineal

# Panel 4: histograma de la Componente 1 del PCA con kernel, que muestra la separación
for value, name, color in classes:                                                     # Se recorre cada clase
    ax_hist.hist(Y_kpca[labels == value, 0], bins=25, color=color,
                 alpha=0.75, label=name)                                               # Histograma de la clase
ax_hist.set_title("Component 1 of Gaussian kernel PCA")  # Título del panel
ax_hist.set_xlabel("Component 1")                        # Nombre del eje horizontal
ax_hist.set_ylabel("Number of observations")             # Nombre del eje vertical
ax_hist.grid(alpha=0.3)                                  # Cuadrícula suave
ax_hist.legend(loc="best", frameon=True)                 # Leyenda con las dos clases

plt.tight_layout()                                       # Evita que se solapen los textos
plt.show()                                               # Muestra la figura

• El PCA lineal no separa las clases: las circunferencias son casi isotrópicas, por lo que las componentes solo rotan los ejes y el resultado es prácticamente idéntico a los datos originales.

• El PCA con kernel gaussiano (\(\sigma=0.3\)) separa las clases con la Componente 1 por sí sola, mediante un umbral cercano a 0, porque equivale a un PCA lineal en un espacio de características donde la distancia radial sí es una dirección lineal.

  • Círculo interno (rojo): puntos muy similares entre sí en el espacio del kernel, con su estructura angular a lo largo de la Componente 2.

  • Círculo externo (azul): puntos poco similares entre sí, cuya varianza se dispersa en muchas direcciones y se colapsa en un grupo compacto.

• Precauciones: los signos de las componentes son arbitrarios, las distancias absolutas del panel 3 no tienen unidades interpretables y las etiquetas solo colorean, pues el método es no supervisado.

• Sensibilidad a \(\sigma\): un valor muy grande recupera el PCA lineal y uno muy pequeño lleva a \(K \to I\) sin estructura útil. Aquí \(\sigma=0.3\) es del orden del radio interno y menor que el externo, por lo que funciona bien.

Tarea 10: verificación numérica y análisis

Enunciado. Usando el código anterior como punto de partida, realice los siguientes experimentos y redacte un breve informe con sus conclusiones.

• Compruebe numéricamente la Proposición 3 (inciso 3): calcule model["Kc"] @ np.ones(n) y el rango numérico de Kc con np.linalg.matrix_rank. Relacione el resultado con la demostración de la Tarea 3.

• Compruebe la Proposición 2 (inciso 2) con un kernel lineal: construya \(K=XX^{T}\) para un conjunto de datos centrado, y compare los autovalores de \(K/n\) con los de la matriz de varianza-covarianza \(S\) calculada con np.cov(X.T, bias=True).

• Varíe \(\sigma\) en \(\{0{,}05;\,0{,}1;\,0{,}3;\,1;\,5\}\) y grafique las dos primeras componentes en cada caso. Describa cómo cambia la separabilidad de las dos circunferencias y relacione sus observaciones con los casos límite descritos en las consideraciones prácticas.

• Verifique la Tarea 9: transforme un punto nuevo con kernel_pca_transform y compare con el cálculo directo de \(C^{T}\boldsymbol{k}_c(\boldsymbol{x})\) usando la forma vectorial que usted demostró.

Verificación. Todas las comprobaciones deben cumplirse salvo errores de redondeo del orden de \(10^{-8}\) a \(10^{-12}\).

Síntesis de la sección

El PCA con kernels reemplaza el problema de autovalores de la matriz de varianza-covarianza, de orden \(p\) o \(r\), por el problema de autovalores de la matriz de Gram centrada \(K_c\), de orden \(n\) (Proposiciones 1 a 3). El kernel trick permite calcular \(K_c\) sin conocer explícitamente la transformación \(\Phi\) (Proposición 4), y el centrado en el espacio de características se realiza de forma exacta mediante \(K_c=H\mathbf{K}H\) (Proposición 5). Las componentes resultantes son lineales en el espacio de características y no lineales en el espacio de entrada.

Tarea 10: verificación numérica y análisis

Enunciado. Usando el código anterior como punto de partida, realice los siguientes experimentos y redacte un breve informe con sus conclusiones.

• Compruebe numéricamente la Proposición 3 (inciso 3): calcule model["Kc"] @ np.ones(n) y el rango numérico de Kc con np.linalg.matrix_rank. Relacione el resultado con la demostración de la Tarea 3.

• Compruebe la Proposición 2 (inciso 2) con un núcleo lineal: construya \(K=XX^{T}\) para un conjunto de datos centrado, y compare los autovalores de \(K/n\) con los de la matriz de varianza-covarianza \(S\) calculada con np.cov(X.T, bias=True).

• Varíe \(\sigma\) en \(\{0{,}05;\,0{,}1;\,0{,}3;\,1;\,5\}\) y grafique las dos primeras componentes en cada caso. Describa cómo cambia la separabilidad de las dos circunferencias y relacione sus observaciones con los casos límite descritos en las consideraciones prácticas.

• Verifique la Tarea 9: transforme un punto nuevo con kernel_pca_transform y compare con el cálculo directo de \(C^{T}\boldsymbol{k}_c(\boldsymbol{x})\) usando la forma vectorial que usted demostró.

Verificación. Todas las comprobaciones deben cumplirse salvo errores de redondeo del orden de \(10^{-8}\) a \(10^{-12}\).

Síntesis de la sección

El PCA con núcleos reemplaza el problema de autovalores de la matriz de varianza-covarianza, de orden \(p\) o \(r\), por el problema de autovalores de la matriz de Gram centrada \(K_c\), de orden \(n\) (Proposiciones 1 a 3). El truco del núcleo permite calcular \(K_c\) sin conocer explícitamente la transformación \(\Phi\) (Proposición 4), y el centrado en el espacio de características se realiza de forma exacta mediante \(K_c=H\mathbf{K}H\) (Proposición 5). Las componentes resultantes son lineales en el espacio de características y no lineales en el espacio de entrada.

7.9. Implementación

• Hasta este momento, hemos analizado en detalle estimadores de aprendizaje supervisado: aquellos estimadores que predicen etiquetas basadas en datos de entrenamiento etiquetados. Ahora, empezamos a examinar varios estimadores no supervisados, los cuales pueden resaltar aspectos interesantes de los datos sin hacer referencia a etiquetas conocidas.

• En esta sección, exploramos lo que posiblemente es uno de los algoritmos no supervisados más ampliamente utilizados: el análisis de componentes principales (PCA). PCA es fundamentalmente un algoritmo de reducción de dimensionalidad, pero también puede ser útil como herramienta de visualización, para filtrado de ruido, extracción y construcción de características, y mucho más.

import warnings
warnings.filterwarnings('ignore')

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()

7.10. Introducción al análisis de componentes principales

El análisis de componentes principales (PCA) es una técnica no supervisada, rápida y adaptable, diseñada para reducir la dimensionalidad de los datos. La forma más sencilla de comprender su funcionamiento es a través del examen de un conjunto de datos bidimensional. Tomemos en consideración la recopilación posterior de 200 puntos de datos

rng = np.random.RandomState(1)
X = np.dot(rng.rand(2, 2), rng.randn(2, 200)).T
plt.scatter(X[:, 0], X[:, 1])
plt.axis('equal');

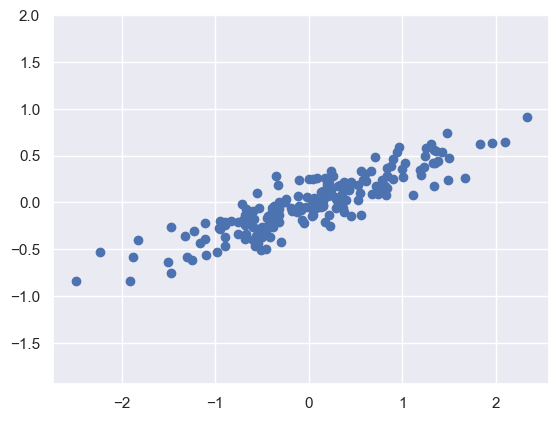
• Visualmente, es evidente que existe una conexión casi lineal entre las variables \(x\) e \(y\). En lugar de intentar predecir los valores de \(y\) basándose en los valores de \(x\), el objetivo del aprendizaje no supervisado aquí es comprender la conexión entre los valores de \(x\) e \(y\).

• El análisis de componentes principales (PCA) cuantifica esta conexión identificando los ejes principales dentro de los datos y utilizándolos para representar el conjunto de datos. Para realizar esto utilizando el estimador PCA de scikit-learn, siga estos pasos:

from sklearn.decomposition import PCA

pca = PCA(n_components=2)
pca.fit(X)

PCA(n_components=2)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

• El proceso de ajuste extrae información crucial de los datos, principalmente los "componentes" y la "varianza explicada".

print(pca.components_)

[[-0.94446029 -0.32862557]
 [-0.32862557  0.94446029]]

print(pca.explained_variance_)

[0.7625315 0.0184779]

• Para comprender el significado de estos valores, podemos representarlos visualmente como vectores situados sobre los datos de entrada. En esta representación, los "componentes" determinan la dirección del vector, mientras que la "varianza explicada" determina el cuadrado de la longitud del vector.

def draw_vector(v0, v1, ax=None):
    ax = ax or plt.gca()
    arrowprops=dict(arrowstyle='->',
                    linewidth=2,
                    shrinkA=0, shrinkB=0, color='r')
    ax.annotate('', v1, v0, arrowprops=arrowprops)

plt.scatter(X[:, 0], X[:, 1], alpha=0.5)
for length, vector in zip(pca.explained_variance_, pca.components_):
    v = vector * 3 * np.sqrt(length)
    draw_vector(pca.mean_, pca.mean_ + v)
plt.axis('equal');

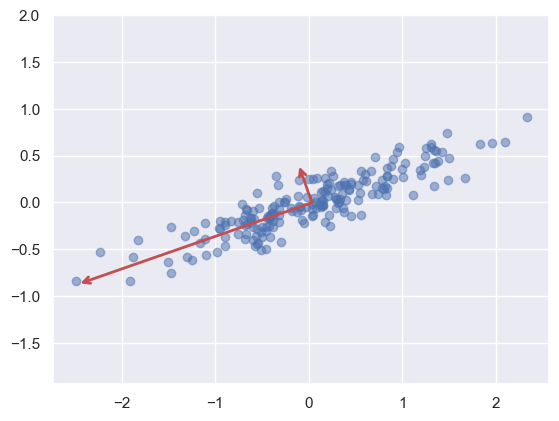
Observation 7.1

• Estos vectores simbolizan las orientaciones primarias de los datos, y la longitud del vector indica la importancia de esa orientación para explicar la distribución de los datos. Esta longitud cuantifica la varianza de los datos cuando se proyectan sobre esa orientación. La proyección de los puntos de datos sobre estas orientaciones principales se denomina "componentes principales" de los datos.

7.10.1. PCA para reducción de dimensión

• El PCA puede emplearse para reducir la dimensionalidad anulando uno o varios de los componentes principales más pequeños. De este modo se obtiene una representación de los datos de menor dimensión, conservando al mismo tiempo la mayor varianza posible de los datos. A continuación se muestra un ejemplo de utilización de PCA com transformación para la reducción de la dimensionalidad`

pca = PCA(n_components=1)
pca.fit(X)
X_pca = pca.transform(X)
print("original shape:   ", X.shape)
print("transformed shape:", X_pca.shape)

original shape:    (200, 2)
transformed shape: (200, 1)

• Los datos se han transformado y ahora existen en una sola dimensión. Para comprender las implicaciones de esta reducción de la dimensionalidad, podemos invertir el proceso de transformación en estos datos reducidos y luego compararlos con los datos iniciales trazándolos juntos

X_new = pca.inverse_transform(X_pca)
plt.scatter(X[:, 0], X[:, 1], alpha=0.5)
plt.scatter(X_new[:, 0], X_new[:, 1], alpha=0.8)
plt.axis('equal');

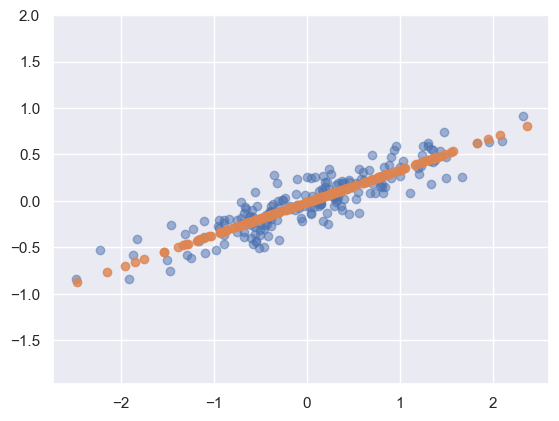
• Los puntos más claros en azul representan los datos iniciales, mientras que los más oscuros en salmon representan la versión proyectada. Esta comparación visual aclara el concepto que subyace a la reducción de la dimensionalidad de PCA: consiste en eliminar los datos a lo largo del eje o ejes principales menos significativos, conservando únicamente el componente o componentes con mayor varianza.

• El grado de reducción de la varianza (relacionado con la dispersión de los puntos alrededor de la línea en la figura) indica aproximadamente el grado de "información" descartada en esta reducción de la dimensionalidad. A pesar de que la dimensionalidad se ha reducido a la mitad, este nuevo conjunto de datos es, en varios aspectos, suficientemente eficaz para captar las conexiones primarias entre los puntos de datos. Las relaciones fundamentales entre los puntos de datos se conservan en gran medida.

7.10.2. PCA para visualización: Dígitos escritos a mano

• El valor de reducir la dimensionalidad puede no ser del todo evidente en sólo dos dimensiones, pero se hace mucho más evidente cuando se trata de datos de alta dimensionalidad. Para ilustrarlo, examinaremos la aplicación de PCA al conjunto de datos de dígitos escritos a mano (imágenes \(8\times8\) (64-dimensional) de píxeles enteros en el rango \(0,\dots,16\).).

from sklearn.datasets import load_digits
from distinctipy import distinctipy

digits = load_digits(as_frame=True)

digits.data.shape

(1797, 64)

plt.matshow(digits.images[1]);

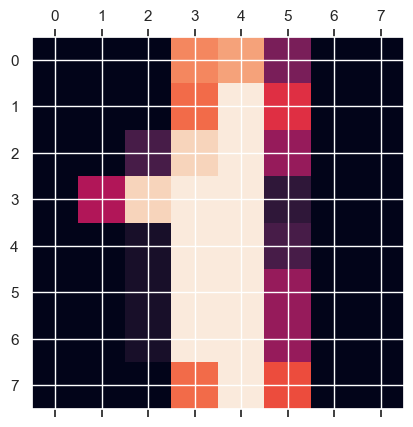
digits.images[1]

array([[ 0.,  0.,  0., 12., 13.,  5.,  0.,  0.],
       [ 0.,  0.,  0., 11., 16.,  9.,  0.,  0.],
       [ 0.,  0.,  3., 15., 16.,  6.,  0.,  0.],
       [ 0.,  7., 15., 16., 16.,  2.,  0.,  0.],
       [ 0.,  0.,  1., 16., 16.,  3.,  0.,  0.],
       [ 0.,  0.,  1., 16., 16.,  6.,  0.,  0.],
       [ 0.,  0.,  1., 16., 16.,  6.,  0.,  0.],
       [ 0.,  0.,  0., 11., 16., 10.,  0.,  0.]])

digits.data.head()

	pixel_0_0	pixel_0_1	pixel_0_2	pixel_0_3	pixel_0_4	pixel_0_5	pixel_0_6	pixel_0_7	pixel_1_0	pixel_1_1	...	pixel_6_6	pixel_6_7	pixel_7_0	pixel_7_1	pixel_7_2	pixel_7_3	pixel_7_4	pixel_7_5	pixel_7_6	pixel_7_7
0	0.0	0.0	5.0	13.0	9.0	1.0	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0	6.0	13.0	10.0	0.0	0.0	0.0
1	0.0	0.0	0.0	12.0	13.0	5.0	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0	0.0	11.0	16.0	10.0	0.0	0.0
2	0.0	0.0	0.0	4.0	15.0	12.0	0.0	0.0	0.0	0.0	...	5.0	0.0	0.0	0.0	0.0	3.0	11.0	16.0	9.0	0.0
3	0.0	0.0	7.0	15.0	13.0	1.0	0.0	0.0	0.0	8.0	...	9.0	0.0	0.0	0.0	7.0	13.0	13.0	9.0	0.0	0.0
4	0.0	0.0	0.0	1.0	11.0	0.0	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0	0.0	2.0	16.0	4.0	0.0	0.0

5 rows × 64 columns

digits.data.describe()

	pixel_0_0	pixel_0_1	pixel_0_2	pixel_0_3	pixel_0_4	pixel_0_5	pixel_0_6	pixel_0_7	pixel_1_0	pixel_1_1	...	pixel_6_6	pixel_6_7	pixel_7_0	pixel_7_1	pixel_7_2	pixel_7_3	pixel_7_4	pixel_7_5	pixel_7_6	pixel_7_7
count	1797.0	1797.000000	1797.000000	1797.000000	1797.000000	1797.000000	1797.000000	1797.000000	1797.000000	1797.000000	...	1797.000000	1797.000000	1797.000000	1797.000000	1797.000000	1797.000000	1797.000000	1797.000000	1797.000000	1797.000000
mean	0.0	0.303840	5.204786	11.835838	11.848080	5.781859	1.362270	0.129661	0.005565	1.993879	...	3.725097	0.206455	0.000556	0.279354	5.557596	12.089037	11.809126	6.764051	2.067891	0.364496
std	0.0	0.907192	4.754826	4.248842	4.287388	5.666418	3.325775	1.037383	0.094222	3.196160	...	4.919406	0.984401	0.023590	0.934302	5.103019	4.374694	4.933947	5.900623	4.090548	1.860122
min	0.0	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	...	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
25%	0.0	0.000000	1.000000	10.000000	10.000000	0.000000	0.000000	0.000000	0.000000	0.000000	...	0.000000	0.000000	0.000000	0.000000	1.000000	11.000000	10.000000	0.000000	0.000000	0.000000
50%	0.0	0.000000	4.000000	13.000000	13.000000	4.000000	0.000000	0.000000	0.000000	0.000000	...	1.000000	0.000000	0.000000	0.000000	4.000000	13.000000	14.000000	6.000000	0.000000	0.000000
75%	0.0	0.000000	9.000000	15.000000	15.000000	11.000000	0.000000	0.000000	0.000000	3.000000	...	7.000000	0.000000	0.000000	0.000000	10.000000	16.000000	16.000000	12.000000	2.000000	0.000000
max	0.0	8.000000	16.000000	16.000000	16.000000	16.000000	16.000000	15.000000	2.000000	16.000000	...	16.000000	13.000000	1.000000	9.000000	16.000000	16.000000	16.000000	16.000000	16.000000	16.000000

8 rows × 64 columns

digits.data.isna().any().any()

False

color_bars = ['black', 'red', 'green', 'blue', 'cyan', 'purple', 'orange', 'pink', 'brown', 'yellow']

digits.target.value_counts().plot(kind='bar', color=distinctipy.get_colors(10));

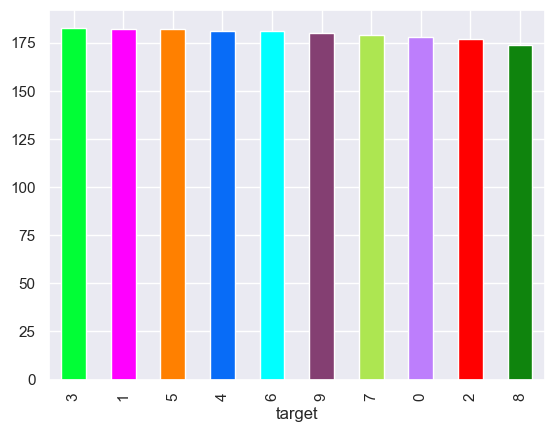
• Para comprender mejor las conexiones entre estos puntos, podemos utilizar el PCA para condensarlos en un número de dimensiones más manejable, por ejemplo, dos dimensiones (proyectar de 64 a 2 dimensiones)

import pandas as pd

pca = PCA(2)
projected = pca.fit_transform(digits.data)
print(digits.data.shape)
print(projected.shape)

(1797, 64)
(1797, 2)

• El trazado de los dos componentes principales iniciales de cada punto nos permite extraer información de los datos.

plt.scatter(projected[:, 0], projected[:, 1],
            c=digits.target, edgecolor='none', alpha=0.7,
            cmap=plt.cm.get_cmap('viridis', 10));
plt.xlabel('PC 1');
plt.ylabel('PC 2');
plt.colorbar();

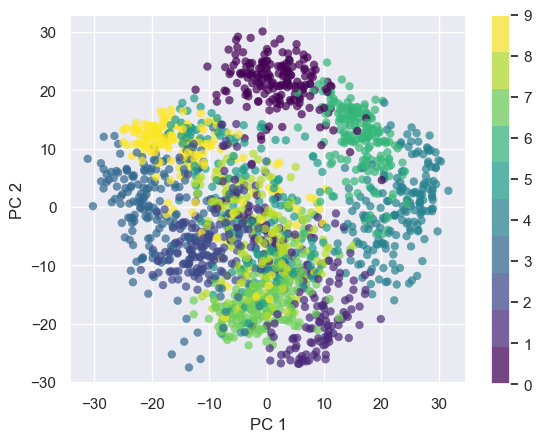
Observation 7.2

• Consideremos la importancia de estos componentes: el conjunto completo de datos forma una nube de puntos de 64 dimensiones, y estos puntos concretos representan la proyección de cada punto de datos a lo largo de las direcciones con mayor varianza.

• Fundamentalmente, hemosidentificado el estiramiento y la rotación más eficaces en el espacio de 64 dimensiones, lo que nos permite observar la disposición de los dígitos en dos dimensiones. Y lo que es más importante, esto se ha logrado de forma no supervisada, sin utilizar ninguna etiqueta.

• El PCA puede conceptualizarse como la selección de funciones base óptimas. La combinación de sólo un pequeño subconjunto de estas funciones basta para reconstruir eficazmente la mayoría de los elementos del conjunto de datos. Los componentes principales, que sirven de representación condensada de los datos en dimensiones inferiores, son esencialmente los coeficientes que escalan cada elemento de esta serie. PCA nos permite recuperar las características más destacadas de la imagen de entrada ¡con sólo una media más ocho componentes! La cantidad de cada píxel en cada componente es el corolario de la orientación del vector en nuestro ejemplo bidimensional.

7.10.3. Selección del número de componentes

• Un aspecto esencial de la aplicación práctica del PCA consiste en determinar el número óptimo de componentes necesarios para caracterizar los datos. Esto puede lograrse analizando la proporción de varianza explicada acumulativa en relación con el número de componentes

pca = PCA().fit(digits.data)
plt.plot(np.cumsum(pca.explained_variance_ratio_))
plt.xlabel('number of components')
plt.ylabel('cumulative explained variance');

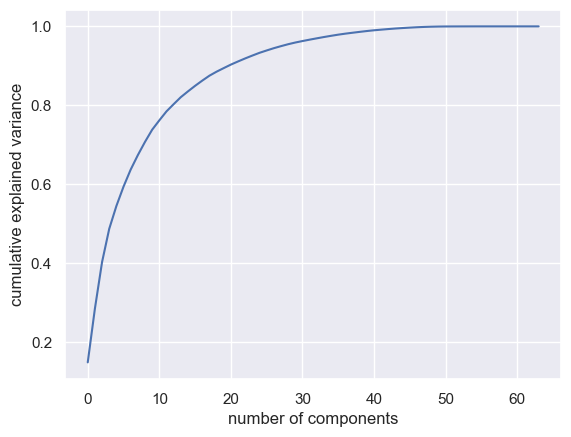
• La curva presentada proporciona una medida de qué parte de la varianza total, que abarca 64 dimensiones, queda englobada por los \(N\) componentes iniciales. Por ejemplo, en el caso de los dígitos, los 10 componentes iniciales representan aproximadamente el 75\% de la varianza, mientras que se necesitan unos 50 componentes para describir casi el 100\% de la varianza.

• De ello se desprende que nuestra proyección bidimensional conlleva una pérdida significativa de información, como demuestra la varianza explicada. Para conservar aproximadamente el 90\% de la varianza, serían necesarios unos 20 componentes. El análisis de este gráfico para un conjunto de datos con dimensiones elevadas ayuda a comprender el grado de redundancia presente en numerosas observaciones.

7.10.4. PCA como filtro de ruido

• El PCA puede servir como técnica para filtrar el ruido de los datos. El concepto fundamental es que los componentes con una varianza significativamente mayor que el impacto del ruido, están menos influidas por éste. Por consiguiente, si se reconstruyen los datos utilizando el subconjunto primario de componentes principales con la mayor varianza, se conserva efectivamente la señal al tiempo que se elimina el ruido.

• Para observar esto en acción con el conjunto de datos de dígitos, empezaremos generando gráficos para varias instancias de los datos originales libres de ruido

digits = load_digits()

def plot_digits(data):
    fig, axes = plt.subplots(4, 10, figsize=(10, 4),
                             subplot_kw={'xticks':[], 'yticks':[]},
                             gridspec_kw=dict(hspace=0.1, wspace=0.1))
    for i, ax in enumerate(axes.flat):
        ax.imshow(data[i].reshape(8, 8),
                  cmap='binary', interpolation='nearest', clim=(0, 16))

plot_digits(digits.data)

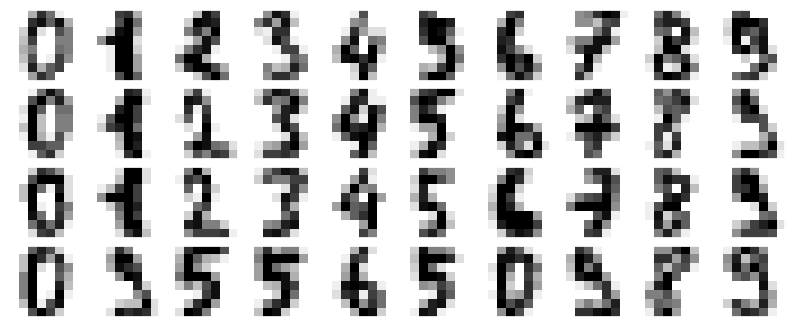
• Ahora, introduciremos ruido aleatorio para generar un conjunto de datos con ruido y, a continuación, volveremos a crear los gráficos

np.random.seed(42)
noisy = np.random.normal(loc=digits.data, scale=4)
plot_digits(noisy)

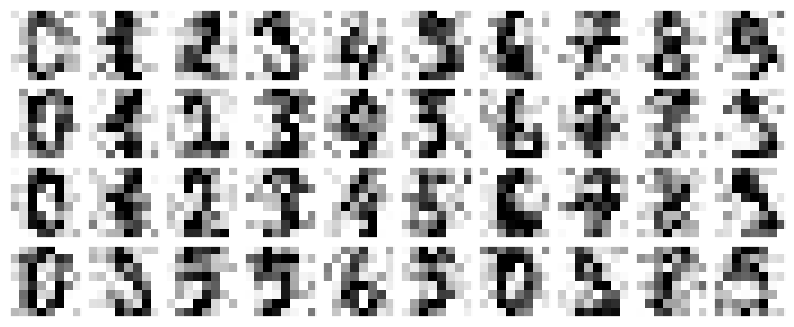
• Las imágenes muestran un ruido evidente e incluyen píxeles erróneos. Procederemos entrenando un PCA sobre los datos ruidosos, especificando que la proyección debe mantener el 50% de la varianza

pca = PCA(0.50).fit(noisy)
pca.n_components_

12

• En este caso, el 50% de la varianza corresponde a 12 componentes principales. Para proceder, calculamos estos componentes y posteriormente utilizamos la inversa del proceso de transformación para reconstruir los dígitos filtrados

components = pca.transform(noisy)
filtered = pca.inverse_transform(components)
plot_digits(filtered)

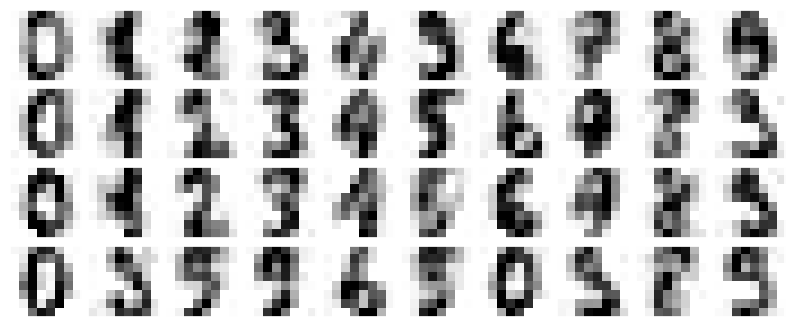
• La capacidad de PCA para retener señales y filtrar el ruido la convierte en una técnica muy valiosa para la selección de características. Por ejemplo, en lugar de entrenar un clasificador en datos con numerosas dimensiones, se puede optar por entrenar el clasificador en la representación de dimensiones reducidas, que elimina intrínsecamente el ruido aleatorio de las entradas.

7.10.5. Ejemplo Eigenfaces

• Examinamos la utilización de una proyección PCA como selector de características en el contexto del reconocimiento facial. Profundicemos en los detalles, trabajado con el conjunto de datos Labeled Faces in the Wild proporcionado por scikit-learn

from sklearn.datasets import fetch_lfw_people
faces = fetch_lfw_people(min_faces_per_person=60)
print(faces.target_names)
print(faces.images.shape)

['Ariel Sharon' 'Colin Powell' 'Donald Rumsfeld' 'George W Bush'
 'Gerhard Schroeder' 'Hugo Chavez' 'Junichiro Koizumi' 'Tony Blair']
(1348, 62, 47)

• min_faces_per_person=60 asegura que solo se incluyan personas con al menos 60 imágenes disponibles en el conjunto de datos. (1348, 62, 47) está asociado con el shape de las imágenes de los rostros en el conjunto de datos. Indica que hay 1348 imágenes en total. Cada imagen tiene dimensiones de 62 píxeles de alto por 47 píxeles de ancho. Esto significa que cada imagen tiene una resolución de 62x47 píxeles y que hay 1348 imágenes en total en el conjunto de datos.

• A continuación examinaremos los ejes principales que engloban este conjunto de datos. Debido a su considerable tamaño, emplearemos randomized PCA. Este enfoque emplea una técnica aleatoria para aproximar rápidamente los \(N\) componentes principales iniciales, lo que resulta especialmente ventajoso para datos de gran dimensión, como éste, con casi 3.000 dimensiones. Nos centraremos en los primeros 150 componentes

pca = PCA(150, svd_solver='randomized')
pca.fit(faces.data)

PCA(n_components=150, svd_solver='randomized')

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

• En este caso, resulta interesante representar visualmente las imágenes correspondientes a los componentes principales iniciales. Formalmente denominados "vectores propios", estos componentes suelen denominarse "caras propias" cuando se trata de imágenes. Como se muestra en la figura, estas caras propias tienen un aspecto bastante inquietante

fig, axes = plt.subplots(3, 8, figsize=(9, 4),
                         subplot_kw={'xticks':[], 'yticks':[]},
                         gridspec_kw=dict(hspace=0.1, wspace=0.1))
for i, ax in enumerate(axes.flat):
    ax.imshow(pca.components_[i].reshape(62, 47), cmap='bone')

• Nótese que las caras propias iniciales (empezando por la parte superior izquierda) parecen estar relacionadas con el ángulo de iluminación de la cara, mientras que los vectores principales posteriores empiezan a aislar rasgos específicos como los ojos, la nariz y los labios. Examinemos ahora la varianza acumulada asociada a estos componentes para calibrar hasta qué punto la proyección conserva la información de los datos

plt.plot(np.cumsum(pca.explained_variance_ratio_))
plt.xlabel('number of components')
plt.ylabel('cumulative explained variance');

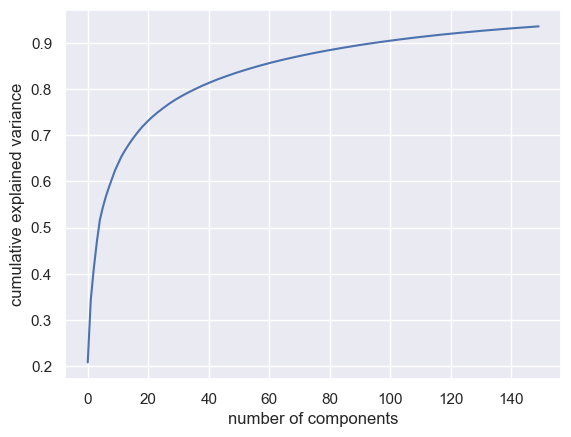
• Se observa que estos 150 componentes abarcan algo más del 90% de la varianza. Esto sugiere que, utilizando estos 150 componentes, probablemente recuperaríamos la mayoría de los atributos críticos de los datos. Para consolidar esta idea, podemos comparar las imágenes de entrada originales con las imágenes reconstruidas utilizando estos 150 componentes

pca = PCA(150, svd_solver='randomized').fit(faces.data)
components = pca.transform(faces.data)
projected = pca.inverse_transform(components)

fig, ax = plt.subplots(2, 10, figsize=(10, 2.5),
                       subplot_kw={'xticks':[], 'yticks':[]},
                       gridspec_kw=dict(hspace=0.1, wspace=0.1))
for i in range(10):
    ax[0, i].imshow(faces.data[i].reshape(62, 47), cmap='binary_r')
    ax[1, i].imshow(projected[i].reshape(62, 47), cmap='binary_r')
    
ax[0, 0].set_ylabel('full-dim\ninput')
ax[1, 0].set_ylabel('150-dim\nreconstruction');

• Las imágenes de la fila superior representan la entrada original, mientras que la fila inferior muestra imágenes reconstruidas utilizando sólo 150 de las aproximadamente 3.000 características iniciales. Esta visualización ilustra eficazmente por qué la selección de características PCA, logra un éxito significativo.

• A pesar de reducir significativamente la dimensionalidad de los datos en aproximadamente un factor de 20, las imágenes proyectadas conservan suficiente información para que podamos reconocer a los individuos en las imágenes mediante inspección visual.

• Esto implica que nuestro algoritmo de clasificación puede entrenarse con datos de 150 dimensiones en lugar de con datos de 3.000 dimensiones. Dependiendo del algoritmo específico elegido, esto puede conducir a una clasificación mucho más eficiente.