15. Soluciones a ejercicios

Autoria de soluciones

• A continuación, se presentan las soluciones a algunos ejercicios propuestos en las distintas secciones de estas notas de clase. Cada solución incluirá el enlace de LinkedIn de los estudiantes del Pregrado en Ciencia de Datos que los resolvieron como parte de la evaluación del curso.

• Para cualquier corrección, duda o inquietud, se puede contactar directamente al autor del ejercicio o, en su defecto, al responsable de los apuntes del curso de Machine Learning, Lihki Rubio, PhD.

Sección: Random Forest y XGBoost

Ejercicio 6

Solución propuesta por: Kanery Marcela Camargo Rodriguez, DS. y Valentina Esther Cabrera De la Rosa, DS.

Paso 1: Evaluación del cambio de impureza para cada característica (variable)

Variable 1: Age

• Se observa que esta variable es de tipo numérico. Por consiguiente, antes de calcular los índices correspondientes, es fundamental establecer los umbrales que definirán las condiciones o categorías que caracterizan dicha variable. Para este propósito, se empleará la siguiente fórmula, la cual está vinculada a la mediana.

\[\text{Umbral} = \frac{x_i + x_{(i+1)}}{2}\]

• De este modo, se obtienen los siguientes valores: $\(27, 33, 36, 39, 43, 45, 46.5, 47, 49\)$

• Para calcular el índice de Gini en función de cada umbral, se seguirá un procedimiento sistemático con el objetivo de identificar el umbral que minimiza la impureza. Los pasos a seguir son los siguientes:

1. Definir el umbral: Seleccionar un valor que sirva como punto de partición para dividir las observaciones en dos grupos.

2. Segmentar los datos en función del umbral:

   • Grupo 1: Observaciones en las que la edad es menor que el umbral.

   • Grupo 2: Observaciones en las que la edad es mayor o igual al umbral.

3. Determinar la distribución de las observaciones en cada grupo:

   • Contabilizar la cantidad de observaciones en cada grupo.

4. Clasificar las observaciones por categoría en cada grupo:

   • Contar cuántas observaciones pertenecen a la clase SI (1) y cuántas a la clase NO (0) dentro de la variable objetivo binaria.

5. Calcular el índice de Gini para cada grupo:

   • Aplicar la fórmula del índice de Gini en cada subconjunto, considerando las proporciones de las clases SI y NO.

6. Calcular el índice de Gini ponderado para el umbral:

   • Obtener el índice de Gini total combinando los valores calculados en los grupos, ponderados por el número de observaciones en cada uno.

• Este procedimiento se repite para cada posible umbral, seleccionando aquel que genere la mayor reducción en la impureza. A continuación, se presenta el análisis detallado para cada umbral.

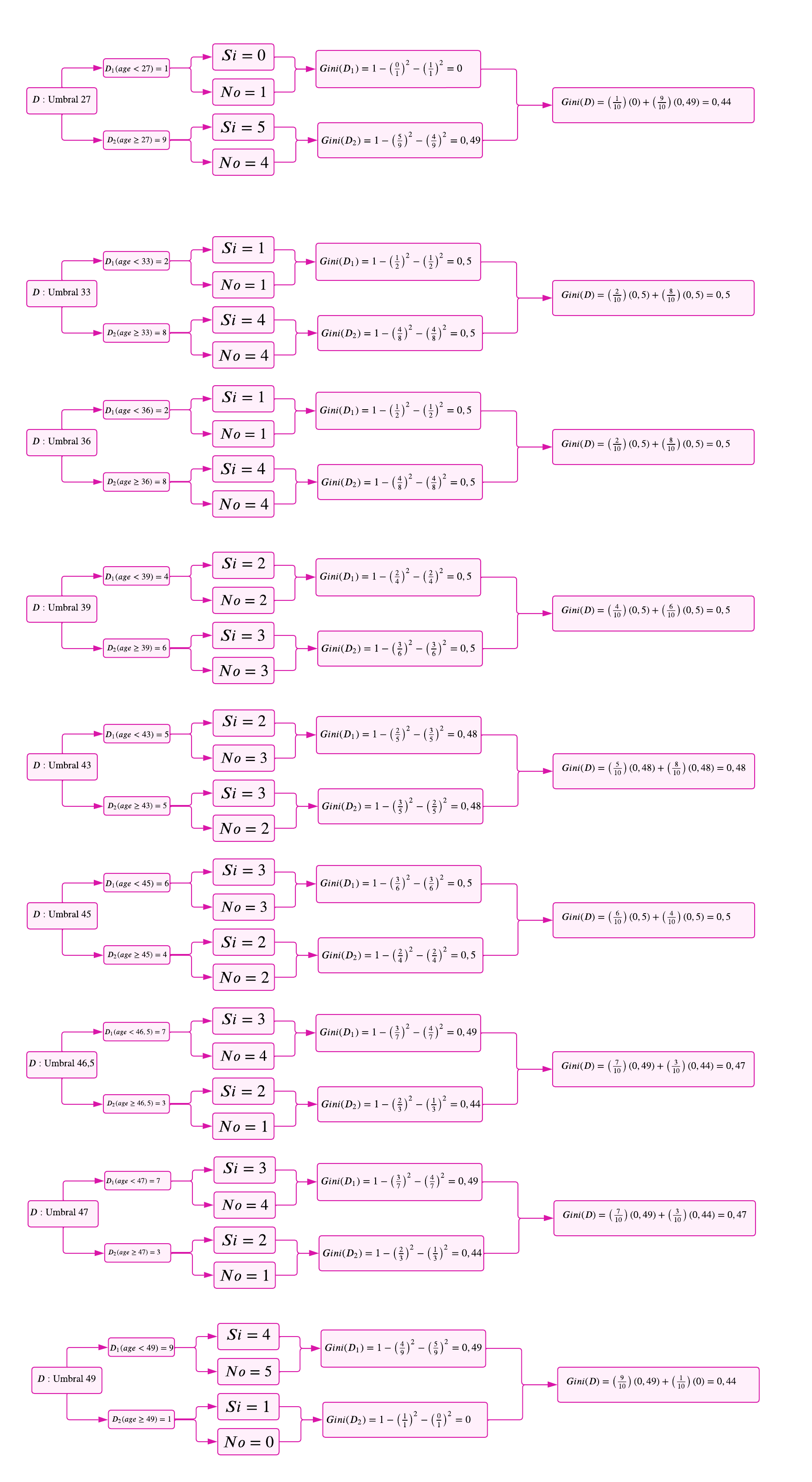
• En este caso, el umbral que presenta el menor índice de Gini es 27. En situaciones donde exista un empate entre varios umbrales, se seleccionará el primero que alcance dicho valor. Procedamos ahora con el análisis de las demás variables.

Variable 2: Like Dogs

• A continuación, se analiza la segunda característica o variable, Like Dogs, la cual es de tipo binario. El procedimiento a seguir es similar al utilizado para la variable numérica; sin embargo, en este caso, la segmentación se realiza directamente sobre los dos valores posibles: SI (1) y NO (0). Los pasos para el cálculo del índice de Gini son los siguientes:

1. Segmentar los datos en función de la variable binaria:

   • Grupo 1: Observaciones en las que Like Dogs es SI (1).

   • Grupo 2: Observaciones en las que Like Dogs es NO (0).

2. Determinar la distribución de las observaciones en cada grupo:

   • Contabilizar la cantidad de observaciones en cada grupo.

3. Clasificar las observaciones según la variable objetivo:

   • Contar cuántas observaciones pertenecen a la clase SI (1) y cuántas a la clase NO (0) dentro de cada grupo.

4. Calcular el índice de Gini para cada grupo:

   • Aplicar la fórmula del índice de Gini considerando las proporciones de las clases SI y NO en la variable objetivo.

5. Calcular el índice de Gini ponderado:

   • Obtener el índice de Gini total combinando los valores calculados en ambos grupos, ponderados por la cantidad de observaciones en cada uno.

6. Seleccionar la división óptima:

   • La partición con el menor índice de Gini representará la mejor segmentación en términos de reducción de impureza.

• Este análisis permitirá evaluar el impacto de la variable binaria Like Dogs en la reducción de la impureza y su relevancia en la construcción del modelo.

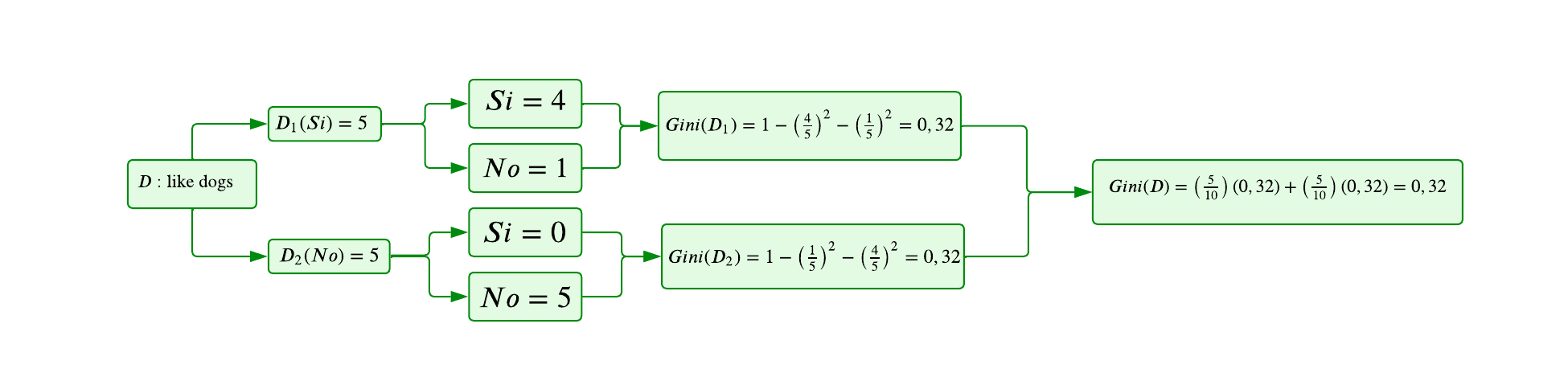
Variable 3: Like gravity

• Ahora, para la última variable (Like gravity) procedemos de la misma manera que con la anterior variable.

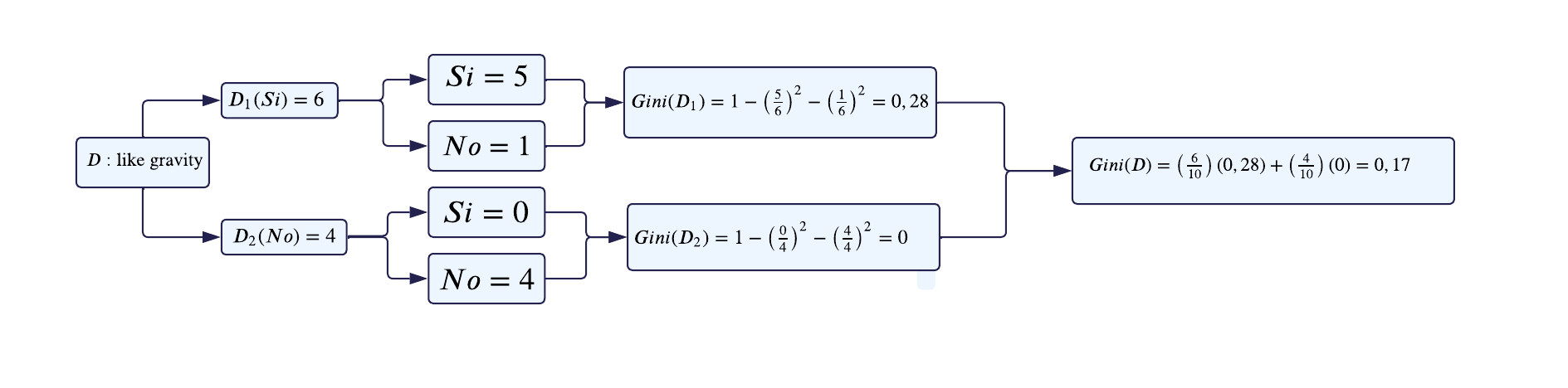
• Después de analizar el cambio de impureza para cada variable, se observa que el menor valor corresponde a la variable Like Gravity (0.17). Por lo tanto, esta será seleccionada como nuestro nodo padre.

• Además, dentro de este nodo padre, identificamos un nodo puro, que se caracteriza por tener un índice de Gini igual a 0. Esto significa que, dentro de la categoría correspondiente a la clase NO, se puede establecer directamente que Gonna Be an Astronaut es igual a NO. Es decir, si Like Gravity es NO, entonces Gonna Be an Astronaut también será NO.

Paso 2: Construcción del árbol luego de haber encontrado el nodo padre

• Para continuar con la construcción del árbol, seguimos estos pasos:

1. Filtrar las observaciones correspondientes a la clase SI en la variable Like Gravity:

   • Esto crea un subconjunto de datos (nodo no nulo) donde solo se consideran las observaciones en las que Like Gravity es SI.

2. Repetir el proceso de partición:

   • Aplicar los mismos pasos que en la etapa anterior: evaluar el cambio de impureza para las variables restantes y seleccionar la mejor partición para dividir aún más el nodo actual.

• Este enfoque iterativo garantiza que el árbol se construya de manera óptima, dividiendo en cada nivel de acuerdo con la variable que maximice la pureza del nodo resultante.

• Teniendo en cuenta lo anterior, la nueva tabla para realizar los cálculos queda de la siguiente manera:

Age	Like Dogs	Gonna Be an Astronaut
30	1	1
36	0	1
44	1	1
47	1	1
47	0	1
51	1	0

Variable 1: Age

• Procedemos de manera similar al Paso 1, con la diferencia de que los umbrales cambian debido a que ahora trabajamos únicamente con las 6 observaciones filtradas del nodo anterior. Este ajuste garantiza que los cálculos sean específicos para el subconjunto de datos resultante y continúen optimizando la partición en función del índice de Gini.

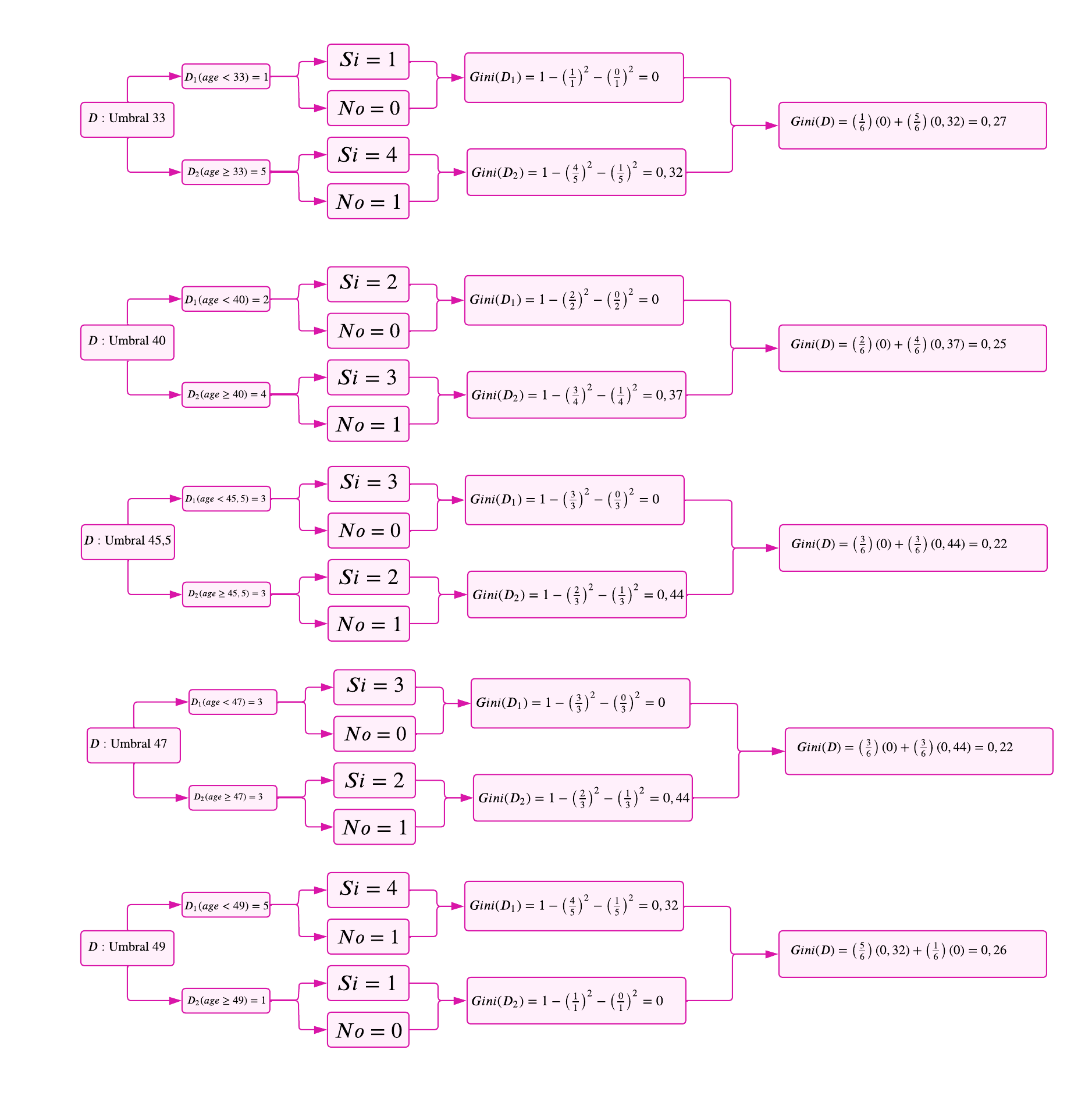
• En este caso, el umbral con el índice de Gini más bajo es Umbral 45,5 (0,22)

Variable 2: Like dogs

• Ahora, analizaremos la variable Like Dogs tras la filtración realizada en el nodo padre.

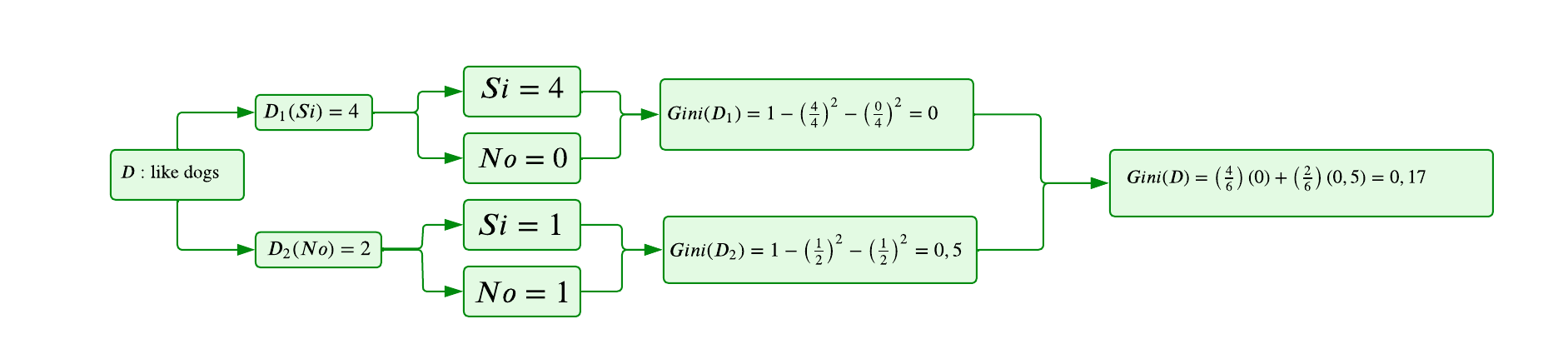
• Nótese que el índice de Gini para esta variable es igual a 0,17. En este paso, observamos que la variable con el menor índice de Gini es Like Dogs. Por lo tanto, esta variable se selecciona como el siguiente nodo del árbol, ya que permite una mayor reducción en la impureza del nodo actual y contribuye a una partición más pura en el árbol de decisión.

Paso 3: Construcción del árbol final

• Ahora, al filtrar los datos según la variable Like Dogs, observamos que solo queda una característica disponible, la cual es la edad. Por lo tanto, esta se convierte en el siguiente nodo del árbol. Este nodo se genera a partir de la clase NO de la variable Like Dogs, dado que la clase SI es un nodo hoja. En este caso, se define que si te gusta la gravedad y te gustan los perros, entonces sí vas a ser astronauta.

• Finalmente, dado que el umbral con el menor índice de Gini es 45,5, la edad se utiliza como criterio de partición. La edad menor a 45,5 se convierte en el siguiente nodo, donde ambas clases derivadas se convierten en nodos hoja:

1. Clase SI (Nodo hoja):

   • Si te gusta la gravedad, no te gustan los perros, pero tienes menos de 45,5 años, entonces vas a ser astronauta.

2. Clase NO (Nodo hoja):

   • Si te gusta la gravedad, no te gustan los perros, pero tienes más de 45,5 años, entonces no vas a ser astronauta.

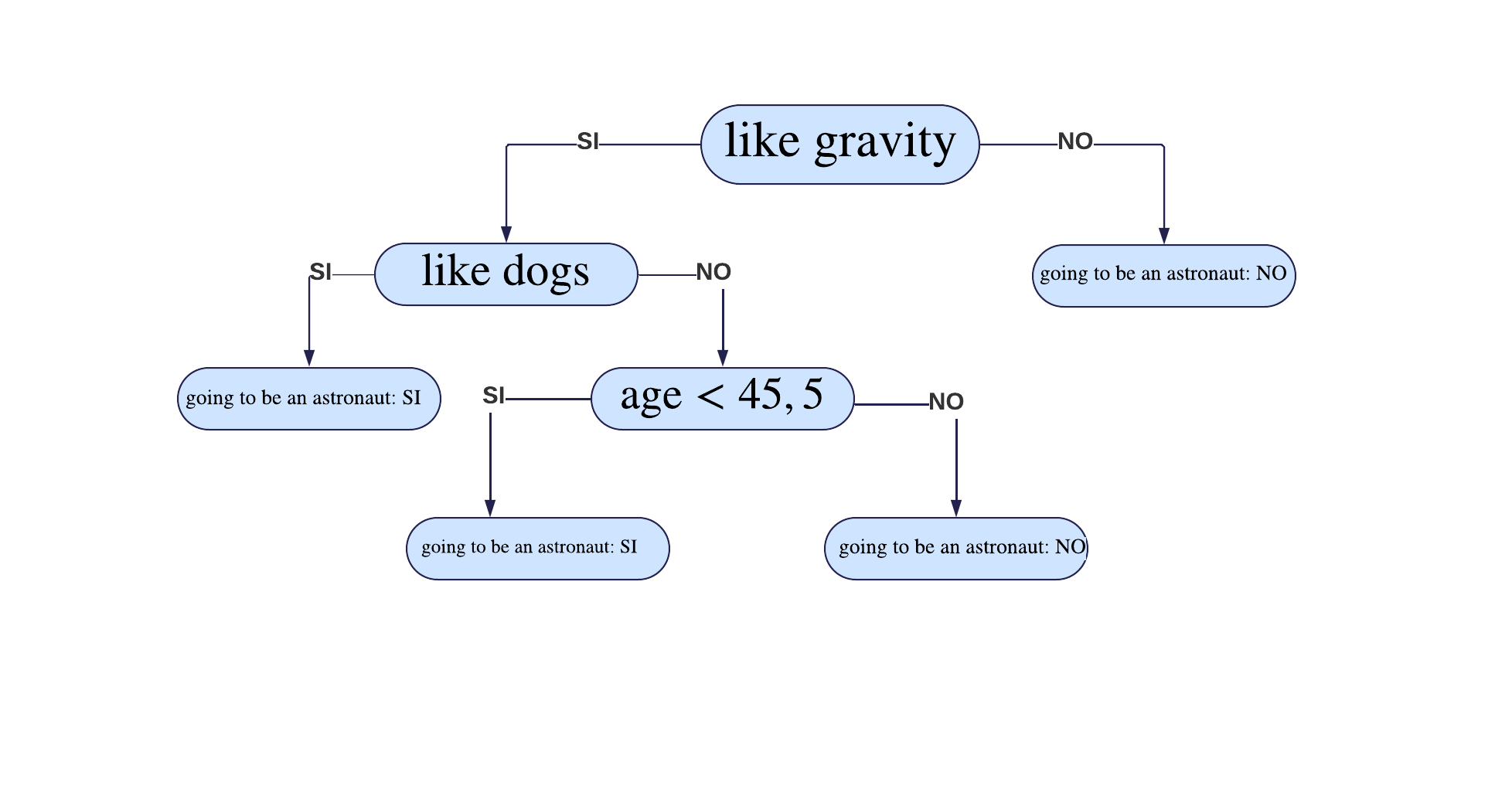
• Finalmente, así se completa la construcción del árbol de decisión, asegurando que cada nodo optimice la pureza en función de las variables disponibles.