2. \(k\)-vecinos más cercanos#
Introducción
El algoritmo vecino más cercano es considerado uno de los más simples dentro del aprendizaje automático. Su enfoque consiste en memorizar el conjunto de entrenamiento y luego predecir la etiqueta del vecino más cercano en dicho conjunto. Este método se basa en la idea de que las características utilizadas para describir los puntos en el dominio son relevantes para determinar sus etiquetas, de manera que es probable que puntos cercanos tengan la misma etiqueta. Incluso en situaciones donde el conjunto de entrenamiento es muy grande, es posible encontrar un vecino más cercano, como por ejemplo cuando el conjunto de entrenamiento abarca toda la Web y las distancias se basan en enlaces.
A diferencia de otros paradigmas algorítmicos que requieren hipótesis predefinidas, el método del vecino más cercano calcula una etiqueta para cualquier punto de prueba sin buscar un predictor dentro de una clase de funciones predefinida. En este capítulo, se describen los métodos del vecino más cercano tanto para problemas de clasificación como de regresión, se analiza su rendimiento en clasificación binaria y se discute la eficacia de su aplicación.
2.1. Análisis#
Definition 2.1 (\(k\)-NN (Clasificación))
Sea \(\mathcal{X}\) nuestro dominio de instancia (conjunto de objetos que se desea etiquetar), dotado con una métrica \(\rho\). Es decir, \(\rho:\mathcal{X}\times\mathcal{X}\longrightarrow\mathbb{R}\) es una función que retorna la distancia entre cualquier par de elementos de \(\mathcal{X}\). Por ejemplo, si \(\mathcal{X}=\mathbb{R}^{d}\), entonces \(\rho\) puede ser la distancia Euclidiana,
Sea \(S=(\boldsymbol{x}_{1}, y_{1}),\dots,(\boldsymbol{x}_{m}, y_{m})\) una secuencia de ejemplos de entrenamiento y \(\mathcal{Y}\), el conjunto de etiquetas, usualmente: \(\{0, 1\},~\{-1, +1\}\) o \(\mathbb{R}\). Para cada \(\boldsymbol{x}\in\mathcal{X}\), sea \(\pi_{1}(\boldsymbol{x}),\dots,\pi_{m}(\boldsymbol{x})\) una reordenación de \(\{1,\dots,m\}\) en función de su distancia a \(\boldsymbol{x}\), \(\rho(\boldsymbol{x}, \boldsymbol{x}_{i})\). Esto es, para todo \(i<m\),
Para un número \(k\), la regla \(k\)-NN para la clasificación binaria se define del siguiente modo:
input: muestra de entrenamiento \(S=(\boldsymbol{x}_{1}, y_{1}),\dots,(\boldsymbol{x}_{m}, y_{m})\)output: \(\forall~\boldsymbol{x}\in\mathcal{X}\), etiqueta mayoritaria en \(\{y_{\pi_{i}(\boldsymbol{x})}:~i\leq k\}\)
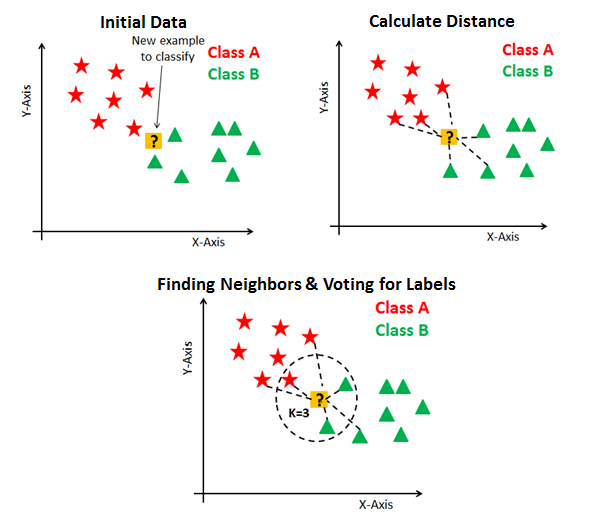
Fig. 2.1 Clasificación usando \(k\)-NN para \(k=3\). Source: kdnuggets.com.#
Desempate en la clasificación\(k\)-NN: En ocasiones ocurren empates a la hora de seleccionar la clase mayoritaria. Existen varias formas de abordar este problema, las siguientes son las más frecuentes.
1. Elija un \(k\) diferente
Nótese que, aunque un método de clasificación de tres vecinos más cercanos soluciona el problema de la selección de vecinos en las Fig. 2.2 i) y ii), el problema de la Fig. 2.2 iii) no es resuelto cuando se consideran por ejemplo cuatro. Elegir un \(k\) diferente, no siempre es la mejor solución.
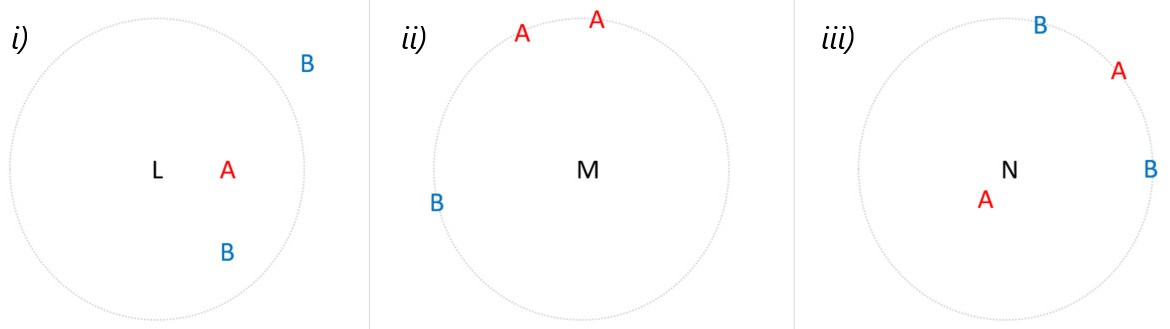
Fig. 2.2 k-NN: Empates respecto a distancia, en la selección de clase con mayor frecuencia.#
2. Elija al azar entre los valores empatados
Aplicando este enfoque a la Fig. 2.2 ii), cada una de las tres observaciones tendría la misma probabilidad de ser seleccionada como uno de los vecinos más cercanos.
En la Fig. 2.2 iii), se seleccionaría \(A\) como el vecino más cercano a \(N\), y uno de los tres puntos observados restantes se seleccionaría al azar.
Dependiendo de cuáles de los valores empatados se permitan en el modelo, podría tener un efecto significativo en cómo se clasifica \(N\).
3. Permitir observaciones hasta el punto de parada natural
La idea aquí es elegir el valor de \(k\geq 2\) más pequeño tal que, no existan empates
Para la Fig. 2.2 i), se seleccionarían las dos observaciones más cercanas, nótese que, para \(k=3\) se tiene un empate. Para la Fig. 2.2 ii), como hay un empate para \(k=3\), se consideran los tres vecinos más cercanos. La restricción de solo dos vecinos se elimina para esta observación en particular.
Del mismo modo, en la Fig. 2.2 iii) se seleccionan las cuatro observaciones. Observe que este método elegiría tantos valores como fuera necesario para evitar el empate. Si en la Fig. 2.2 ii) hubiera ocho puntos equidistantes, se incluirían los ocho en el modelo.
4. Con base en vecinos seleccionados
Supongamos que nos hemos decidido por el tercer método y que ya tenemos nuestros vecinos seleccionados
Elegir un\(k\)impar: Algunos sugieren simplemente elegir un valor impar para \(k\). Este método no siempre funciona, ya que los estados de clasificación también podrían ser impares \((A, B, C)\).Elegir al azar entre vecinos empatados. Con este método, \(L\) (considerando \(k=2\)) y \(N\) (considerando \(k=4\)) tienen la misma probabilidad de ser clasificados como \(A\) o \(B\). Pero, ¿es justo el azar? ¿Tiene sentido que \(N\), que está muy cerca de \(A\), tenga la misma probabilidad de ser \(B\)?Ponderación por distancia. Para resolver el problema planteado por el método anterior, es posible ponderar los vecinos de modo que los más cercanos al punto no observado tengan un “mayor voto”. Este método daría lugar a que tanto \(L\) como \(N\) se clasificaran como \(A\), ya que los vecinos \(A\) están más cerca que los demás en comparación.
Predictor: Definamos por \(h_{S}(\boldsymbol{x})\) la regla de predicción (el subíndice \(S\) hace hincapié en el hecho de que el predictor de salida depende de \(S\)). Esta función también se denomina predictor, hipótesis o clasificador. El predictor puede utilizarse para predecir la etiqueta de nuevos puntos de dominio. Cuando \(k=1\) (ver Definition 2.1), tenemos la regla \(1\)-NN:
Nótese que hemos considerado la métrica Euclideana en esta definición, pero, dependiendo del conjunto de datos, podría ser mas adecuado utilizar una métrica diferente (ver Manhatan, Minkowski). Esto es, una métrica alternativa, podría mejorar los errores cometidos por el clasificador.
Definition 2.2 (\(k\)-NN (Regresión))
Para problemas de regresión, a saber, \(\mathcal{Y}=\mathbb{R}\), se puede definir la regla de predicción como la media objetivo de los \(k\) vecinos más cercanos. Esto es,
Más en general, para alguna función \(\phi:~(\mathcal{X}, \mathcal{Y})^{k}\rightarrow\mathcal{Y}\), la regla \(k\)-NN con respecto a \(\phi\) es:
Se puede verificar que podemos lanzar la predicción por mayoría de etiquetas (clasificación) o por el objetivo promediado (regresión) como en la Ecuación (2.1) mediante una elección adecuada de \(\phi\).
La generalidad puede llevar a otras reglas, por ejemplo, si \(\mathcal{Y}=\mathbb{R}\), podemos tomar una media ponderada de los objetivos según la distancia a \(x\)
Definition 2.3 (Error empírico y verdadero revisado)
Para una distribución de probabilidad, \(\mathcal{D}\), sobre \(\mathcal{X}\times\mathcal{Y}\), se puede medir la probabilidad de que \(h\) cometa un error cuando los puntos etiquetados se extraen aleatoriamente según \(\mathcal{D}\). Redefinimos el error verdadero (o riesgo) de una regla de predicción \(h\) como
Minimización Empírica de Riesgo (ERM). Nos gustaría encontrar un predictor, \(h\), para el que se minimizara el error \(L_{\mathcal{D}}(h)\) sobre una clase de hipótesis denota por \(\mathcal{H}\), esto es: \(\text{ERM}_{\mathcal{H}}(S)\in\underset{h\in\mathcal{H}}{\text{argmin}}~L_{S}(h)\). Cada \(h\in\mathcal{H}\) es una función de \(\mathcal{X}\) a \(\mathcal{Y}\).Sin embargo, no se conocen los datos que generan \(\mathcal{D}\). A lo que sí se tiene acceso es a los datos de entrenamiento, \(S\). Una noción útil de error que puede calcular es el error de entrenamiento (riesgo empírico), es decir, el error en el que incurre el clasificador sobre la muestra de entrenamiento:
Dado \(S\), y un aprendizaje, se puede calcular \(L_{S}(h)\) para cualquier función \(h:X\rightarrow\{0,1\}\).
Deseamos encontrar alguna hipótesis, \(h : X\rightarrow Y\), que (probablemente de forma aproximada) minimice el riesgo verdadero,\(L_{D}(h)\).
Predictor óptimo de Bayes: Dada cualquier distribución de probabilidad \(\mathcal{D}\) sobre \(\mathcal{X}\times\{0, 1\}\), la mejor función de predicción de etiquetas de \(\mathcal{X}\) a \(\{0, 1\}\) será
Se puede verificar que para toda distribución de probabilidad \(\mathcal{D}\), el predictor óptimo de Bayes \(f_{D}\) es óptimo, en el sentido de que ningún otro clasificador, \(g : \mathcal \rightarrow\{0, 1\}\), tiene un error menor. Es decir, para cada clasificador \(g, L_{\mathcal{D}}(f_{\mathcal{D}}) \leq L_{\mathcal{D}}(g)\).
Definition 2.4 (Funciones de pérdidas generalizadas)
Dado cualquier conjunto \(\mathcal{H}\) (que desempeña el papel de nuestras hipótesis, o predictor) y algún dominio \(Z\) sea \(\ell\) cualquier función de \(\mathcal{H}\times Z\) al conjunto de los números reales no negativos, \(\ell: \mathcal{H}\times Z\rightarrow\mathbb{R}^{+}\). Llamamos a estas funciones, funciones de pérdida.
Nótese que para los problemas de predicción, tenemos que \(Z = \mathcal{X}\times\mathcal{Y}\). Sin embargo, nuestra noción de la función de pérdida se generaliza más allá de las tareas de predicción y, por tanto, permite que \(Z\) sea cualquier dominio de ejemplos.
Definimos ahora la función de riesgo como la pérdida esperada de un clasificador, \(h\in\mathcal{H}\), con respecto a la distribución de probabilidad \(\mathcal{D}\) sobre \(Z\), a saber,
Es decir, consideramos la esperanza de la pérdida de \(h\) sobre los objetos \(z\) elegidos aleatoriamente de acuerdo con \(\mathcal{D}\). Del mismo modo, definimos el riesgo empírico como la pérdida esperada sobre una muestra dada \(S=(z_{1},\dots,z_{m})\in Z^{m}\), a saber
Ejemplos: Dada una variable aleatoria \(z\) que abarca el conjunto de pares \(\mathcal{X}\times\mathcal{Y}\), definimos las siguientes funciones de pérdida
\(\ell_{\text{0-1}}(h, (x,y))\) se utiliza en problemas de clasificación binaria o multiclase. Hay que tener en cuenta que, para una variable aleatoria, \(\alpha\), que toma los valores \(\{0,1\}\),
\[\mathbb{E}_{\alpha\sim\mathcal{D}}[\alpha] = \mathbb{P}_{\alpha\sim\mathcal{D}}[\alpha = 1].\]Por lo tanto, las funciones de pérdida definidas en Eq. (2.4) y Eq. (2.2) son equivalentes.
Observation 2.1 (\(1\)-NN)
Dado que las reglas NN son métodos de aprendizaje tan naturales, sus propiedades de generalización han sido ampliamente estudiadas. La mayoría de los resultados anteriores son resultados de consistencia asintótica, que analizan el rendimiento de las reglas NN cuando el tamaño de la muestra, \(m\), tiende a \(\infty\), y la tasa de convergencia depende de la distribución subyacente.
Estamos interesados en aprendizajes de muestras de entrenamiento finitas y entender el rendimiento de generalización en función del tamaño de esos conjuntos de entrenamiento finitos y de supuestos previos claros sobre la distribución de los datos. Por lo tanto, presentamos un análisis de muestras finitas de la regla 1-NN.
Generalización de la regla \(1\)-NN
Ahora analizamos el error verdadero de la regla \(1\)-NN para la clasificación binaria con función pérdida \(0-1\) a saber, \(\mathcal{Y}=\{0, 1\}\) y \(\ell(h, (\boldsymbol{x}, y))=\mathbb{1}_{[h(\boldsymbol{x})\neq y]}\). También supondremos en todo el análisis que \(\mathcal{X} = [0,1]^{d}\) y \(\rho\) es la distancia euclidiana.
Empezaremos introduciendo algunas notaciones. Sea \(\mathcal{D}\) una distribución sobre \(\mathcal{X}\times\mathcal{Y}\). Denotemos por \(\mathcal{D}_{\mathcal{X}}\) la distribución marginal inducida por \(\mathcal{X}\) y sea \(\eta:\mathbb{R}^{d}\rightarrow\mathbb{R}\) la probabilidad condicional sobre las etiquetas, esto es,
La regla óptima de Bayes (es decir, la hipótesis que minimiza \(L_{\mathcal{D}}(h)\) sobre todas las funciones \(h\in\mathcal{H}\), ver Eq. (2.3)) es
Suponemos que la función de probabilidad condicional \(\eta\) es \(c\)-Lipschitz (ver Lipschitz continuity) para algún valor de \(c>0\). Es decir, \(\forall~\boldsymbol{x}, \boldsymbol{x}'\in\mathcal{X},~|\eta(\boldsymbol{x})-\eta(\boldsymbol{x}')|\leq c\|\boldsymbol{x}-\boldsymbol{x}'\|\). En otras palabras, esto significa que si dos vectores están próximos, es probable que sus etiquetas sean las mismas.
Nota
El siguiente Lema aplica la Lipschitzness de la función de probabilidad condicional para acotar el error verdadero de la regla 1-NN en función de la distancia entre cada instancia de prueba y su vecino más cercano en el conjunto de entrenamiento.
Lemma 2.1
Sea \(\mathcal{X}=[0,1]^{d},~ \mathcal{Y}=\{0,1\}\), y \(\mathcal{D}\) una distribución sobre \(\mathcal{X}\times\mathcal{Y}\), para la cual, la función de probabilidad condicional, \(\eta\), es una función \(c\)-Lipschitz. Sea \(S=(\boldsymbol{x}_{1}, y_{1}),\dots,(\boldsymbol{x}_{m}, y_{m})\) una muestra iid y sea \(h_{S}\) su correspondiente hipótesis \(1\)-NN. Sea \(h^{\star}\) la regla óptima de Bayes para \(\eta\). Entonces,
Demostración
Dado que \(L_{\mathcal{D}}(h_{S}):=\mathbb{E}_{(\boldsymbol{x}, y)\sim\mathcal{D}}(\ell(h, (\boldsymbol{x}, y)))=\mathbb{E}_{(\boldsymbol{x}, y)\sim\mathcal{D}}(\mathbb{1}_{[h(\boldsymbol{x})\neq y]})\), entonces \(\mathbb{E}(L_{\mathcal{D}}(h_{S})))\) es la probabilidad de muestrear un conjunto de entrenamiento \(S\) y un ejemplo adicional \((\boldsymbol{x}, y)\) tal que, la etiqueta de \(\boldsymbol{x}_{\pi_{1}(\boldsymbol{x})}\) es diferente de \(y\).
En otras palabras, podemos primero muestrear \(m\) ejemplos no etiquetados, \(S_{x}=(x_{1}, x_{2},\dots,x_{m})\), de acuerdo a \(\mathcal{D}_{x}\), y un nuevo ejemplo no etiquetado adicional, \(\boldsymbol{x}\sim\mathcal{D}_{x}\). Luego encontramos \(\boldsymbol{x}_{\pi_{1}(\boldsymbol{x})}\) que es el vecino mas cercano a \(\boldsymbol{x}\) en \(S_{\boldsymbol{x}}\), y finalmente muestrear: \(y\sim\eta(\boldsymbol{x})\) y \(y_{\pi_{1}(\boldsymbol{x})}\sim\eta(\boldsymbol{x}_{\pi_{1}(\boldsymbol{x})})\), donde \(\eta\) es la probabilidad condicional asociada a la distribución marginal sobre \(\mathcal{X},~\mathcal{D}_{x}\).
Entonces
Acotamos superiormente a: \(\underset{y\sim\eta(x), y_{\pi_{1}(x)}\sim\eta(\boldsymbol{x}_{\pi_{1}(\boldsymbol{x})})}{\mathbb{P}}(y\neq y_{\pi_{1}(\boldsymbol{x})}),~\forall~\boldsymbol{x}, \pi_{1}(\boldsymbol{x})\in\mathcal{D}\)
Definamos \(y':=y_{\pi_{1}(\boldsymbol{x})},~x':=\boldsymbol{x}_{\pi_{1}(\boldsymbol{x})}\)
Dado que \(\eta(\boldsymbol{x})=\mathbb{P}(y=1|\boldsymbol{x})\in[0, 1]\), entonces \(|2\eta(\boldsymbol{x})-1|\leq 1\). En efecto:
Dado que \(\eta(\boldsymbol{x})\) es \(c\)-Lipschitz, entonces, \(\forall~\boldsymbol{x},\boldsymbol{x}'\in\mathcal{X},~ |\eta(\boldsymbol{x})-\eta(\boldsymbol{x}')|\leq c\|\boldsymbol{x}-\boldsymbol{x}'\|\). Por lo tanto,
Reemplazando esta última desigualdad en (\(\star\)) se tiene que
Entonces
Dado que \(h^{\star}\) es la regla óptima de Bayes para \(\eta\), entonces \(h^{\star}\) minimiza la pérdida esperada del clasificador, esto es:
Nótese que la desigualdad anterior, que involucra el mínimo \(\min\{\eta(\boldsymbol{x}), 1-\eta(\boldsymbol{x})\}\), es valida. En efecto, si \(\eta(\boldsymbol{x})\in[0, 1]\) y \(\min\{\eta(\boldsymbol{x}), 1-\eta(\boldsymbol{x})\}=\eta(\boldsymbol{x})\), entonces \(\eta(\boldsymbol{x})\leq 1-\eta(\boldsymbol{x})\), por lo tanto:
Por lo tanto:
Observation
El siguiente paso es acotar la distancia entre una variable aleatoria \(\boldsymbol{x}\) y su vecino mas cercano en \(S\). Primero necesitaremos el siguiente Teorema, el cual acota el peso probabilístico de subconjuntos que no son alcanzados por una muestra aleatoria, como una función del tamaño de la muestra.
Lemma 2.2
Sea \(C_{1}, C_{2},\dots,C_{r}\) una colección de subconjuntos de algún dominio \(\mathcal{X}\). Sea \(S\) una sucesión de \(m\) puntos iid muestreados de acuerdo a una distribución de probabilidad \(\mathcal{D}\) sobre \(\mathcal{X}\). Entonces:
Demostración
Por linealidad del valor esperado se tiene que:
Entonces para cada \(i\), usando propiedades de independencia y complemento, dado que \(S\) es una sucesión de \(m\) puntos iid tenemos
Definamos \(\varepsilon=-\mathbb{P}(C_{i})\). Verifiquemos que \(e^{\varepsilon}\ge 1+\varepsilon,~\forall\varepsilon\in\mathbb{R}\). En efecto. Si \(~\varepsilon\leq-1\Rightarrow e^{\varepsilon}>0~\) y \(~1+\varepsilon\leq 0\Rightarrow 1+\varepsilon\leq0<e^{\varepsilon}\Rightarrow1+\varepsilon\leq e^{\varepsilon}\).
\[ \begin{align*} \text{Si}~\varepsilon>-1\Rightarrow e^{\varepsilon}&=\lim_{n\rightarrow\infty}\left(1+\frac{\varepsilon}{n}\right)^{n}\underset{\text{Bernoulli}}{\geq}\lim_{n\rightarrow\infty}1+n\frac{\varepsilon}{n}=1+\varepsilon. \end{align*} \]Entonces \(1+\varepsilon\leq e^{\varepsilon},~\forall\varepsilon\in\mathbb{R}\).
Definition 2.5 (Desigualdad de Bernoulli)
Desigualdad de Bernoulli: Sea \(x\in\mathbb{R}\) tal que \(x>-1\) y \(n\in\mathbb{Z}^{+}\), entonces, \((1+x)^{n}\geq1+nx\).
Dado que \(\varepsilon=-\mathbb{P}(C_{i})\), entonces
De este modo,
Theorem 2.1
Sea \(\mathcal{X}=[0, 1]^{d},~\mathcal{Y}=\{0, 1\}\) y \(\mathcal{D}\) una distribución sobre \(\mathcal{X}\times\mathcal{Y}\) para la cual la función de probabilidad condicional, \(\eta\), es una función \(c\)-Lipschitz. Denotamos con \(h_{S}\) el resultado de aplicar la regla \(1\)-NN a una muestra \(S\sim\mathcal{D}^{m}\). Entonces
Demostración
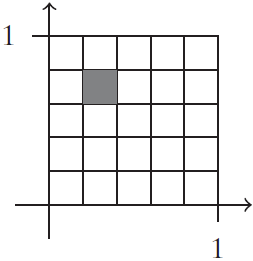
Fijemos \(\varepsilon=1/T\), para algún entero \(T\), sea \(r=T^{d}\), y sea \(C_{1}, C_{2}, \dots, C_{m}\) un cubrimiento del conjunto \(\mathcal{X}\) usando cajas de longitud \(\varepsilon\). Es decir, para cada \((\alpha_{1}, \alpha_{2},\dots,\alpha_{d})\in [T]^{d}\), existe un conjunto \(C_{i}\) de la forma
Entonces, \(\forall~\boldsymbol{x}, \boldsymbol{x}'\) en la misma caja \(\mathcal{B}_{x}\), se tiene que, \(x_{i}-x_{i}'\leq 1/T=\varepsilon\)
Si \(\boldsymbol{x}, \boldsymbol{x}'\) no caen en la misma caja \(\mathcal{B}_{x}\) entonces \(x_{i}-x_{i}'\leq 1,~\forall~i\), entonces \(\|\boldsymbol{x}-\boldsymbol{x}'\|\leq\sqrt{d}\).
Entonces, dado que \(\mathbb{P}\left(\bigcup_{C_{i}\cap S\neq\emptyset}C_{i}\right)\leq1\) y \(\boldsymbol{x}_{\pi_{1}(x)}\in S\)
Dado que \(r=T^{d}=(1/\varepsilon)^{d}=1/\varepsilon^{d}\), entonces:
Usando el Lemma 2.1 se tiene que
Finalmente, fijando \(\varepsilon=2m^{-1/(d+1)}\) se tiene que:
Entonces
Observation 2.2
El Teorema implica que si primero fijamos la distribución generadora de datos y luego hacemos tender \(m\) a infinito, entonces el error de la regla \(1\)-NN converge al doble del error de Bayes. El análisis puede generalizarse a valores mayores que \(k\), demostrando que el error esperado de la regla \(k\)-NN converge a \((1+\sqrt{8/k})\) veces el error del clasificador de Bayes.
2.2. Ejercicios#
En este ejercicio, demostrará el siguiente teorema para la regla \(k\)-NN.
Theorem 2.2
Sea \(\mathcal{X} = [0,1]^d\), \(\mathcal{Y} = \{0,1\}\) y \(D\) una distribución sobre \(\mathcal{X} \times \mathcal{Y}\) tal que la función de probabilidad condicional \(\eta\) es una función \(c\)-Lipschitz. Sea \(h_S\) el resultado de aplicar la regla de los \(k\)-vecinos más cercanos (\(k\)-NN) a una muestra \(S \sim \mathcal{D}^m\), donde \(k \geq 10\). Sea \(h^*\) la hipótesis óptima de Bayes. Entonces,
Parte 1: Demuestre el siguiente Lema
Lemma 2.3
Sea \(C_1, \dots, C_r\) una colección de subconjuntos de un conjunto dominio \(\mathcal{X}\). Sea \(S\) una secuencia de \(m\) puntos muestreados de manera independiente e idénticamente distribuida (i.i.d.) según alguna distribución de probabilidad \(\mathcal{D}\) sobre \(\mathcal{X}\). Entonces, para todo \(k \geq 2\), se cumple que:
\[ \mathbb{E}_{S \sim \mathcal{D}^m} \left[ \sum_{i : |C_i \cap S| < k} \mathbb{P}[C_i] \right] \leq \frac{2rk}{m}. \]
Sugerencia
Demostrar que
\[ \mathbb{E}\left[\sum_{i:|C_i \cap S| < k} \mathbb{P}[C_i]\right] = \sum_{i=1}^r \mathbb{P}[C_i] \mathbb{P}_S[|C_i \cap S| < k]. \]Fijar algún \(i\) y suponer que \(k < \mathbb{P}[C_i] m/2\). Usar el Lemma 2.5 para demostrar que
\[ \mathbb{P}_S[|C_i \cap S| < k] \leq \mathbb{P}_S\left[|C_i \cap S| < \mathbb{P}[C_i] m/2\right] \leq e^{-\mathbb{P}[C_i]m/8}. \]Usar la desigualdad \(\max_a a e^{-ma} \leq 1/me\) para demostrar que, para tal \(i\), tenemos
\[ \mathbb{P}[C_i] \mathbb{P}_S[|C_i \cap S| < k] \leq \mathbb{P}[C_i] e^{-\mathbb{P}[C_i]m/8} \leq \frac{8}{me}. \]Concluir la demostración utilizando el hecho de que, en el caso de \(k \geq \mathbb{P}[C_i]m/2\), claramente tenemos:
\[ \mathbb{P}[C_i] \mathbb{P}_S[|C_i \cap S| < k] \leq \mathbb{P}[C_i] \leq \frac{2k}{m}. \]
Parte 2: Utilizamos la notación \(y \sim p\) como una abreviatura para indicar que “\(y\) es una variable aleatoria de Bernoulli con valor esperado \(p\)”. Demuestre el siguiente lema:
Lemma 2.4
Sea \(k \geq 10\) y sean \(Z_1, \dots, Z_k\) variables aleatorias independientes de Bernoulli con \(\mathbb{P}[Z_i = 1] = p_i\). Denotemos por \(p = \frac{1}{k} \sum_{i} p_i\) y \(p' = \frac{1}{k} \sum_{i=1}^k Z_i\). Se debe demostrar que:
Sugerencia
Sin pérdida de generalidad, supongamos que \(p \leq 1/2\). Entonces, tenemos que \(\mathbb{P}_{y \sim p} [y \neq \mathbb{1}_{[p > 1/2]}] = p\). Definimos \(y^* = \mathbb{1}_{[p' > 1/2]}\).
A continuación, demuestre que:
Utilizando el Lemma 2.5, podemos demostrar que:
\[ \mathbb{P}[p' > 1/2] \leq e^{-k p h\left(\frac{1}{2p} - 1\right)}, \]donde \(h(a) = (1 + a) \log(1 + a) - a\).
Para concluir la demostración del lema, podemos apoyarnos en la siguiente desigualdad (sin necesidad de demostrarla): Para todo \(p \in [0, 1/2]\) y \(k \geq 10\):
Parte 3
Sea \(p, p' \in [0, 1]\) y \(y' \in \{0, 1\}\). Demuestre que:
Parte 4
Concluya la demostración del teorema de acuerdo con los siguientes pasos:
Tal como en la demostración del Theorem 2.1, sea \(\varepsilon > 0\) y sea \(\{C_1, \dots, C_r\}\) la cubierta del conjunto \(\mathcal{X}\) utilizando cajas de longitud \(\varepsilon\). Para cada par de puntos \(x, x' \in C_i\), tenemos que \(\|x - x'\| \leq \sqrt{d} \varepsilon\). En caso contrario, se cumple que \(\|x - x'\| \leq 2\sqrt{d}\).
Demostrar que
(2.5)#\[\begin{split} \begin{align*} \mathbb{E}_S[L_{\mathcal{D}}(h_S)] &\leq \mathbb{E}_S\left[\sum_{i : |C_i \cap S| < k} \mathbb{P}[C_i]\right] \\ &+ \max_i \mathbb{P}_S, (x, y)\left( h_S(x) \neq y \mid \forall j \in [k], \|x - x_{\pi_j(x)}\| \leq \varepsilon \sqrt{d} \right). \end{align*} \end{split}\]
Acotemos el primer sumando usando el Lemma 2.3.
Para acotar el segundo sumando, fijemos \(S|x\) y \(x\) de manera que todos los \(k\) vecinos de \(x\) en \(S|x\) estén a una distancia de a lo sumo \(\varepsilon\sqrt{d}\) de \(x\). Sin pérdida de generalidad, asumamos que los \(k\) vecinos más cercanos son \(x_1, \dots, x_k\). Denotemos \(p_i = \eta(x_i)\) y definamos \(p = \frac{1}{k} \sum_{i} p_i\). Utilizando el Ejercicio (2.5), mostramos que
Sin pérdida de generalidad, asumamos que \(p \leq 1/2\). Ahora, utilizamos el Lemma 2.4 para demostrar que
Además, se puede demostrar que
Combinando todos los resultados anteriores, obtenemos que el segundo sumando en la Ecuación (2.5) está acotado por
Usando \(r = (2/\epsilon)^{d}\), obtenemos
Finalmente, fijando \(\epsilon = 2m^{-1/(d+1)}\) y utilizando
\[ 6c m^{-1/(d+1)} \sqrt{d} + \frac{2k}{e} m^{-1/(d+1)} \leq \left( 6c \sqrt{d} + k \right) m^{-1/(d+1)}, \]se concluye la demostración.
Lemma 2.5 (Límite de Chernoff)
Sea \(Z_1, \dots, Z_m\) un conjunto de variables de Bernoulli independientes, donde para cada \(i\) se cumple que
Definimos \(p = \sum_{i=1}^{m} p_i\) y \(Z = \sum_{i=1}^{m} Z_i\). Entonces, para cualquier \(\delta > 0\), se tiene que
donde
2.3. Implementación#
Clasificación k-vecinos. Como ya se estudió anteriormente, en su versión más sencilla, el algoritmo k-NN solo considera exactamente un vecino más cercano, que es el dato de entrenamiento más cercano al punto para el que queremos hacer una predicción. La predicción es entonces simplemente la etiqueta conocida para este punto de entrenamiento.
import warnings
warnings.filterwarnings('ignore')
import mglearn
import matplotlib
mglearn.plots.plot_knn_classification(n_neighbors=1)
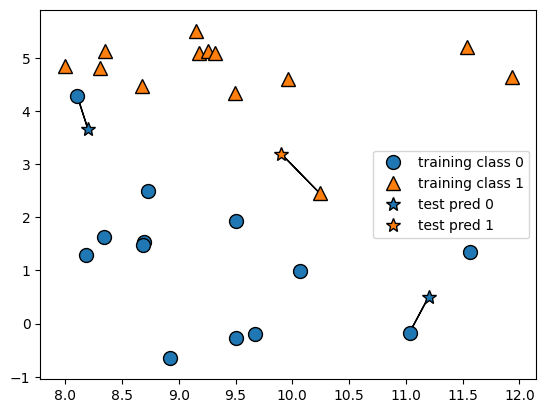
Se han añadido tres nuevos puntos de datos, mostrados como estrellas. Para cada uno de ellos, marcamos el punto más cercano en el conjunto de entrenamiento. La predicción del algoritmo del vecino más cercano es la etiqueta de ese punto (mostrada por el color de la cruz).
En lugar de considerar sólo al vecino más cercano, también podemos considerar un número arbitrario \(k\), de vecinos. De ahí viene el nombre del algoritmo \(k\)-vecinos más cercanos. Cuando se considera más de un vecino, se utiliza la votación para asignar una etiqueta. Esto significa que, para cada punto de prueba, contamos cuántos vecinos pertenecen a clase 0 y cuántos vecinos pertenecen a la clase 1. A continuación, asignamos la clase que es más frecuente: es decir, la clase mayoritaria entre los \(k\) vecinos más cercanos.
mglearn.plots.plot_knn_classification(n_neighbors=3)
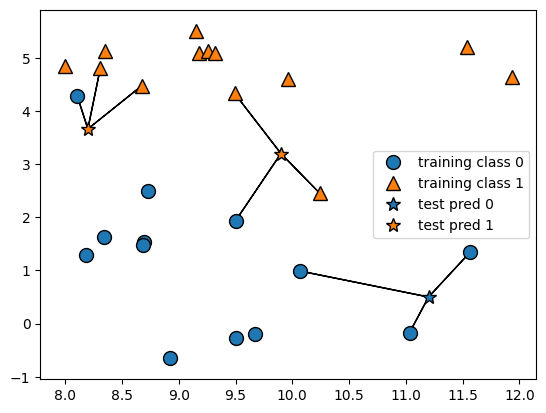
Aunque esta ilustración se refiere a un problema de clasificación binaria, este método puede aplicarse a conjuntos de datos con cualquier número de clases. Para más clases, contamos cuántos vecinos pertenecen a cada clase y volvemos a predecir la clase más común. Ahora veamos cómo podemos aplicar el algoritmo de los vecinos más cercanos utilizando
scikit-learn.En primer lugar, dividimos nuestros datos en un conjunto de entrenamiento y otro de prueba para poder evaluar el rendimiento de la generalización.
random_state=0nos asegura que obtendremos los mismos conjuntos de training y test para diferentes ejecuciones. Para mas información sobresklearn.model_selection.train_test_split(ver documentación train_test_split). Por defecto, cuando no es suministrado el porcentaje de entrenamientotrain_test_splitconsidera este porcentaje para el test como el 25%, esto estest_size=0.25
from sklearn.model_selection import train_test_split
X, y = mglearn.datasets.make_forge()
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
A continuación, importamos e instanciamos la clase
KNeighborsClassifierdesklearnencargada de la tarea de clasificación. Aquí es cuando podemos establecer parámetros, como el número de vecinos a utilizar, el cual consideramos como 3 para este ejemplon_neighbors=3
from sklearn.neighbors import KNeighborsClassifier
clf = KNeighborsClassifier(n_neighbors=3)
Ahora, ajustamos el clasificador utilizando el conjunto de entrenamiento. Para la clase
KNeighborsClassifieresto significa almacenar el conjunto de datos, para poder calcular los vecinos durante la predicción, teniendo en cuenta la asignación de la clase más frecuente, explicada anteriormente
clf.fit(X_train, y_train)
KNeighborsClassifier(n_neighbors=3)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
KNeighborsClassifier(n_neighbors=3)
Para hacer predicciones sobre los datos de prueba, llamamos al método de predicción
predict(). Para cada punto de datos en el conjunto de prueba, éste calcula sus vecinos más cercanos en el conjunto de entrenamiento y encuentra la clase más común entre ellos. Para mas información sobre el cálculo delscore(ver documentación accuracy score)
X_test
array([[11.54155807, 5.21116083],
[10.06393839, 0.99078055],
[ 9.49123469, 4.33224792],
[ 8.18378052, 1.29564214],
[ 8.30988863, 4.80623966],
[10.24028948, 2.45544401],
[ 8.34468785, 1.63824349]])
print("Test set predictions: {}".format(clf.predict(X_test)))
Test set predictions: [1 0 1 0 1 0 0]
print("Test set: {}".format(y_test))
Test set: [1 0 1 0 1 1 0]
Para evaluar lo bien que generaliza nuestro modelo, podemos llamar al método
score()con los datos de prueba junto con las etiquetas de pruebaX_text, y_test.
print("Test set accuracy: {:.2f}".format(clf.score(X_test, y_test)))
Test set accuracy: 0.86
Vemos que nuestro modelo tiene una precisión del 86%, lo que significa que el modelo predijo la clase correctamente para el 86% de las muestras del conjunto de datos de prueba.
2.4. Análisis de KNeighborsClassifier#
Para los conjuntos de datos bidimensionales, también podemos ilustrar la predicción para todos los posibles puntos de prueba en el plano \(xy\). Coloreamos el plano según la clase que se asignaría a un punto en esta región. Esto nos permite ver el límite de decisión (decision boundary) (ver plot_2d_separator), el cual está entre el lugar donde el algoritmo asigna la clase 0 y el lugar donde asigna la clase 1.
import matplotlib.pyplot as plt
fig, axes = plt.subplots(1, 3, figsize=(10, 3))
for n_neighbors, ax in zip([1, 3, 9], axes):
clf = KNeighborsClassifier(n_neighbors=n_neighbors).fit(X, y)
mglearn.plots.plot_2d_separator(clf, X, fill=True, eps=0.5, ax=ax, alpha=.4)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y, ax=ax)
ax.set_title("{} neighbor(s)".format(n_neighbors))
ax.set_xlabel("feature 0")
ax.set_ylabel("feature 1")
axes[0].legend(loc=3)
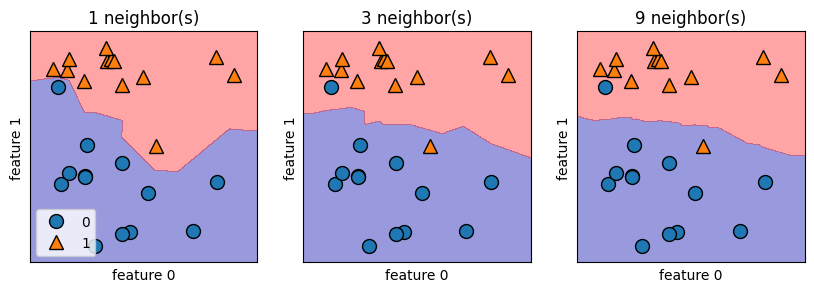
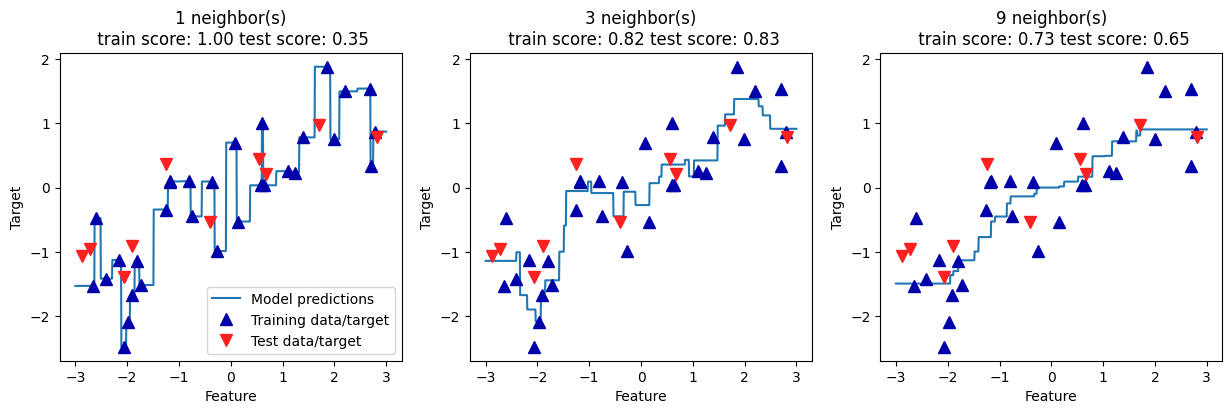
Como se puede ver en la figura de la izquierda, el uso de un solo vecino da como resultado una decisión que sigue de cerca los datos de entrenamiento. La consideración de más vecinos conduce a un límite de decisión más suave. Un límite más suave corresponde a un modelo más sencillo. En otras palabras, el uso de pocos vecinos corresponde a una alta complejidad del modelo (como se muestra en el lado derecho), y el uso de muchos vecinos corresponde a una baja complejidad del modelo.
Si se considera el caso extremo en el que el número de vecinos es el número de todos los puntos de datos del conjunto de entrenamiento, cada punto de prueba tendría exactamente los mismos vecinos (todos puntos de entrenamiento) y todas las predicciones serían las mismas: la clase más frecuente en el conjunto de entrenamiento.
2.5. Aplicación: Breast Cancer Dataset#
Breast Cancer Dataset. Investiguemos si podemos confirmar la conexión entre la complejidad del modelo y la generalización que hemos discutido antes. Lo haremos con el conjunto de datos de cáncer de mama (Breast Cancer) del mundo real.
2.6. Análisis Exploratorio de Datos#
Procedemos a realizar un análisis exploratorio de datos para investigar y resumir principales características de nuestros datos. Primero cargamos nuestro dataset usando la función
load_breast_cancer()desklearn.datasets
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
list(cancer.target_names)
['malignant', 'benign']
list(cancer.feature_names)
['mean radius',
'mean texture',
'mean perimeter',
'mean area',
'mean smoothness',
'mean compactness',
'mean concavity',
'mean concave points',
'mean symmetry',
'mean fractal dimension',
'radius error',
'texture error',
'perimeter error',
'area error',
'smoothness error',
'compactness error',
'concavity error',
'concave points error',
'symmetry error',
'fractal dimension error',
'worst radius',
'worst texture',
'worst perimeter',
'worst area',
'worst smoothness',
'worst compactness',
'worst concavity',
'worst concave points',
'worst symmetry',
'worst fractal dimension']
cancer.data.shape
(569, 30)
cancer.target.shape
(569,)
import pandas as pd
df = pd.DataFrame(cancer.data, columns = cancer.feature_names)
df.insert(0, 'diagnosis', cancer.target)
df.head()
| diagnosis | mean radius | mean texture | mean perimeter | mean area | mean smoothness | mean compactness | mean concavity | mean concave points | mean symmetry | ... | worst radius | worst texture | worst perimeter | worst area | worst smoothness | worst compactness | worst concavity | worst concave points | worst symmetry | worst fractal dimension | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 17.99 | 10.38 | 122.80 | 1001.0 | 0.11840 | 0.27760 | 0.3001 | 0.14710 | 0.2419 | ... | 25.38 | 17.33 | 184.60 | 2019.0 | 0.1622 | 0.6656 | 0.7119 | 0.2654 | 0.4601 | 0.11890 |
| 1 | 0 | 20.57 | 17.77 | 132.90 | 1326.0 | 0.08474 | 0.07864 | 0.0869 | 0.07017 | 0.1812 | ... | 24.99 | 23.41 | 158.80 | 1956.0 | 0.1238 | 0.1866 | 0.2416 | 0.1860 | 0.2750 | 0.08902 |
| 2 | 0 | 19.69 | 21.25 | 130.00 | 1203.0 | 0.10960 | 0.15990 | 0.1974 | 0.12790 | 0.2069 | ... | 23.57 | 25.53 | 152.50 | 1709.0 | 0.1444 | 0.4245 | 0.4504 | 0.2430 | 0.3613 | 0.08758 |
| 3 | 0 | 11.42 | 20.38 | 77.58 | 386.1 | 0.14250 | 0.28390 | 0.2414 | 0.10520 | 0.2597 | ... | 14.91 | 26.50 | 98.87 | 567.7 | 0.2098 | 0.8663 | 0.6869 | 0.2575 | 0.6638 | 0.17300 |
| 4 | 0 | 20.29 | 14.34 | 135.10 | 1297.0 | 0.10030 | 0.13280 | 0.1980 | 0.10430 | 0.1809 | ... | 22.54 | 16.67 | 152.20 | 1575.0 | 0.1374 | 0.2050 | 0.4000 | 0.1625 | 0.2364 | 0.07678 |
5 rows × 31 columns
df_copy = df.copy()
Aquí
0=malignant, 1=benign. Verifiquemos que tipos de datos contiene el dataset. La funcióninfo()proporciona información sobre los tipos de datos, columnas, recuento de valores nulos, uso de memoria, etc.
df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 569 entries, 0 to 568
Data columns (total 31 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 diagnosis 569 non-null int64
1 mean radius 569 non-null float64
2 mean texture 569 non-null float64
3 mean perimeter 569 non-null float64
4 mean area 569 non-null float64
5 mean smoothness 569 non-null float64
6 mean compactness 569 non-null float64
7 mean concavity 569 non-null float64
8 mean concave points 569 non-null float64
9 mean symmetry 569 non-null float64
10 mean fractal dimension 569 non-null float64
11 radius error 569 non-null float64
12 texture error 569 non-null float64
13 perimeter error 569 non-null float64
14 area error 569 non-null float64
15 smoothness error 569 non-null float64
16 compactness error 569 non-null float64
17 concavity error 569 non-null float64
18 concave points error 569 non-null float64
19 symmetry error 569 non-null float64
20 fractal dimension error 569 non-null float64
21 worst radius 569 non-null float64
22 worst texture 569 non-null float64
23 worst perimeter 569 non-null float64
24 worst area 569 non-null float64
25 worst smoothness 569 non-null float64
26 worst compactness 569 non-null float64
27 worst concavity 569 non-null float64
28 worst concave points 569 non-null float64
29 worst symmetry 569 non-null float64
30 worst fractal dimension 569 non-null float64
dtypes: float64(30), int64(1)
memory usage: 137.9 KB
El método
DataFrame.describe()genera estadísticos descriptivos que resumen tendencia central, dispersión y la forma de la distribución de un conjunto de datos, excluyendo los valoresNaN. Una cosa importante es que el método describe() sólo trabaja con valores numéricos. Por lo tanto, si hay algún valor categórico en una columna, el método describe() lo ignorará y mostrará el resumen de las demás columnas, a menos que se pase elparámetro include="all".
df.describe()
| diagnosis | mean radius | mean texture | mean perimeter | mean area | mean smoothness | mean compactness | mean concavity | mean concave points | mean symmetry | ... | worst radius | worst texture | worst perimeter | worst area | worst smoothness | worst compactness | worst concavity | worst concave points | worst symmetry | worst fractal dimension | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 569.000000 | 569.000000 | 569.000000 | 569.000000 | 569.000000 | 569.000000 | 569.000000 | 569.000000 | 569.000000 | 569.000000 | ... | 569.000000 | 569.000000 | 569.000000 | 569.000000 | 569.000000 | 569.000000 | 569.000000 | 569.000000 | 569.000000 | 569.000000 |
| mean | 0.627417 | 14.127292 | 19.289649 | 91.969033 | 654.889104 | 0.096360 | 0.104341 | 0.088799 | 0.048919 | 0.181162 | ... | 16.269190 | 25.677223 | 107.261213 | 880.583128 | 0.132369 | 0.254265 | 0.272188 | 0.114606 | 0.290076 | 0.083946 |
| std | 0.483918 | 3.524049 | 4.301036 | 24.298981 | 351.914129 | 0.014064 | 0.052813 | 0.079720 | 0.038803 | 0.027414 | ... | 4.833242 | 6.146258 | 33.602542 | 569.356993 | 0.022832 | 0.157336 | 0.208624 | 0.065732 | 0.061867 | 0.018061 |
| min | 0.000000 | 6.981000 | 9.710000 | 43.790000 | 143.500000 | 0.052630 | 0.019380 | 0.000000 | 0.000000 | 0.106000 | ... | 7.930000 | 12.020000 | 50.410000 | 185.200000 | 0.071170 | 0.027290 | 0.000000 | 0.000000 | 0.156500 | 0.055040 |
| 25% | 0.000000 | 11.700000 | 16.170000 | 75.170000 | 420.300000 | 0.086370 | 0.064920 | 0.029560 | 0.020310 | 0.161900 | ... | 13.010000 | 21.080000 | 84.110000 | 515.300000 | 0.116600 | 0.147200 | 0.114500 | 0.064930 | 0.250400 | 0.071460 |
| 50% | 1.000000 | 13.370000 | 18.840000 | 86.240000 | 551.100000 | 0.095870 | 0.092630 | 0.061540 | 0.033500 | 0.179200 | ... | 14.970000 | 25.410000 | 97.660000 | 686.500000 | 0.131300 | 0.211900 | 0.226700 | 0.099930 | 0.282200 | 0.080040 |
| 75% | 1.000000 | 15.780000 | 21.800000 | 104.100000 | 782.700000 | 0.105300 | 0.130400 | 0.130700 | 0.074000 | 0.195700 | ... | 18.790000 | 29.720000 | 125.400000 | 1084.000000 | 0.146000 | 0.339100 | 0.382900 | 0.161400 | 0.317900 | 0.092080 |
| max | 1.000000 | 28.110000 | 39.280000 | 188.500000 | 2501.000000 | 0.163400 | 0.345400 | 0.426800 | 0.201200 | 0.304000 | ... | 36.040000 | 49.540000 | 251.200000 | 4254.000000 | 0.222600 | 1.058000 | 1.252000 | 0.291000 | 0.663800 | 0.207500 |
8 rows × 31 columns
Realicemos tabla de frecuencias y diagrama de barras para nuestra variable respuesta
df.diagnosis.value_counts()
diagnosis
1 357
0 212
Name: count, dtype: int64
import seaborn as sns
sns.set_style("whitegrid")
plt.title('Count of cancer type')
sns.countplot(x=df.diagnosis)
plt.xlabel('Diagnosis')
plt.ylabel('Frequency')
plt.show()
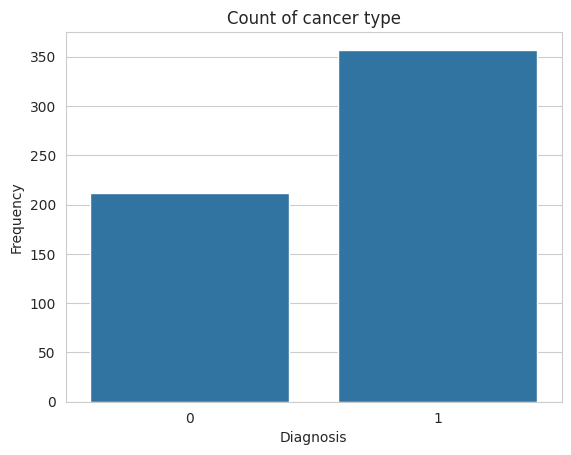
Nótese que nuestro dataset está desbalanceado. Existen técnicas como SMOTE y Stratified sampling, que pueden utilizarse para mejorar el score de clasificación de datos desbalanceados. Utilícela en su proyecto final de investigación. Verifiquemos además si existen datos faltantes en nuestro
Dataframe
df.isnull().sum()
diagnosis 0
mean radius 0
mean texture 0
mean perimeter 0
mean area 0
mean smoothness 0
mean compactness 0
mean concavity 0
mean concave points 0
mean symmetry 0
mean fractal dimension 0
radius error 0
texture error 0
perimeter error 0
area error 0
smoothness error 0
compactness error 0
concavity error 0
concave points error 0
symmetry error 0
fractal dimension error 0
worst radius 0
worst texture 0
worst perimeter 0
worst area 0
worst smoothness 0
worst compactness 0
worst concavity 0
worst concave points 0
worst symmetry 0
worst fractal dimension 0
dtype: int64
Seleccionamos aquellas variables que están correlacionadas con la variable respuesta usando: The Point Biserial Coefficient of Correlation. Para que este método sea efectivo, requiere que las variables explicativas se distribuyan normalmente. Usamos una transformación en el caso que sea necesario
from scipy.stats import pointbiserialr, kstest, norm
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler_params = {}
significant_columns = ['diagnosis']
for column in df.columns[1:]:
D, p_value = kstest(df[column], norm.cdf, args=(df[column].mean(), df[column].std()))
if p_value < 0.05:
scaler.fit(df[column].values.reshape(-1, 1))
scaler_params[column] = (scaler.mean_, scaler.scale_) # Guardar la media y la desviación estándar
df[column] = scaler.transform(df[column].values.reshape(-1, 1))
corr, p_value = pointbiserialr(df[column], df['diagnosis'])
if p_value < 0.05:
significant_columns.append(column)
df_significant = df[significant_columns]
for column, (mean, scale) in scaler_params.items():
if column in df_significant.columns: # Solo revertir las columnas que están en df_significant
df_significant[column] = df_significant[column] * scale + mean # Revertir la normalización
print("\nDataFrame con las columnas significativas y revertidas a su escala original:")
df = df_significant
df.head()
DataFrame con las columnas significativas y revertidas a su escala original:
| diagnosis | mean radius | mean texture | mean perimeter | mean area | mean smoothness | mean compactness | mean concavity | mean concave points | mean symmetry | ... | worst radius | worst texture | worst perimeter | worst area | worst smoothness | worst compactness | worst concavity | worst concave points | worst symmetry | worst fractal dimension | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 17.99 | 10.38 | 122.80 | 1001.0 | 0.11840 | 0.27760 | 0.3001 | 0.14710 | 0.2419 | ... | 25.38 | 17.33 | 184.60 | 2019.0 | 0.1622 | 0.6656 | 0.7119 | 0.2654 | 0.4601 | 0.11890 |
| 1 | 0 | 20.57 | 17.77 | 132.90 | 1326.0 | 0.08474 | 0.07864 | 0.0869 | 0.07017 | 0.1812 | ... | 24.99 | 23.41 | 158.80 | 1956.0 | 0.1238 | 0.1866 | 0.2416 | 0.1860 | 0.2750 | 0.08902 |
| 2 | 0 | 19.69 | 21.25 | 130.00 | 1203.0 | 0.10960 | 0.15990 | 0.1974 | 0.12790 | 0.2069 | ... | 23.57 | 25.53 | 152.50 | 1709.0 | 0.1444 | 0.4245 | 0.4504 | 0.2430 | 0.3613 | 0.08758 |
| 3 | 0 | 11.42 | 20.38 | 77.58 | 386.1 | 0.14250 | 0.28390 | 0.2414 | 0.10520 | 0.2597 | ... | 14.91 | 26.50 | 98.87 | 567.7 | 0.2098 | 0.8663 | 0.6869 | 0.2575 | 0.6638 | 0.17300 |
| 4 | 0 | 20.29 | 14.34 | 135.10 | 1297.0 | 0.10030 | 0.13280 | 0.1980 | 0.10430 | 0.1809 | ... | 22.54 | 16.67 | 152.20 | 1575.0 | 0.1374 | 0.2050 | 0.4000 | 0.1625 | 0.2364 | 0.07678 |
5 rows × 26 columns
Pasamos a verficar si existe correlación entre las características. En caso positivo, removemos multicolinealidad usando el Variance Inflation Factor
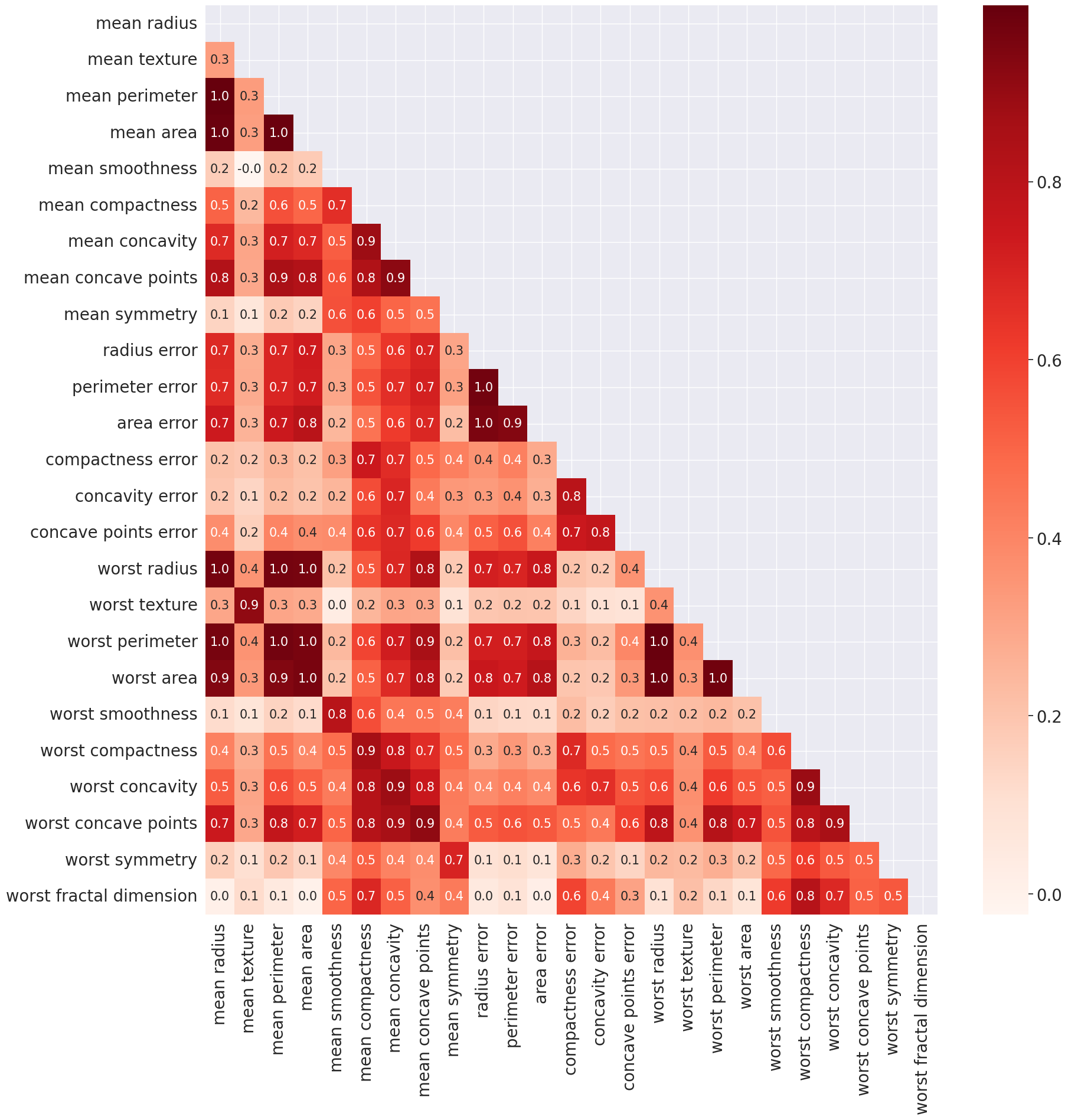
corr = df.iloc[: , 1:].corr()
corr.shape
(25, 25)
import numpy as np
mask = np.zeros_like(corr)
mask[np.triu_indices_from(mask)] = True
sns.set(font_scale=1.8)
plt.figure(figsize=(20,20))
sns.heatmap(corr, mask=mask, cbar=True, fmt='.1f', annot=True, annot_kws={'size':15}, cmap='Reds');
Trazamos histogramas de cada característica en nuestro dataset
melted_data = pd.melt(df, id_vars = "diagnosis",value_vars = ['mean radius', 'mean texture',
'mean perimeter'])
sns.set(font_scale=1.8)
plt.figure(figsize = (20,10))
sns.boxplot(x = "value", y = "variable", hue="diagnosis",data= melted_data);
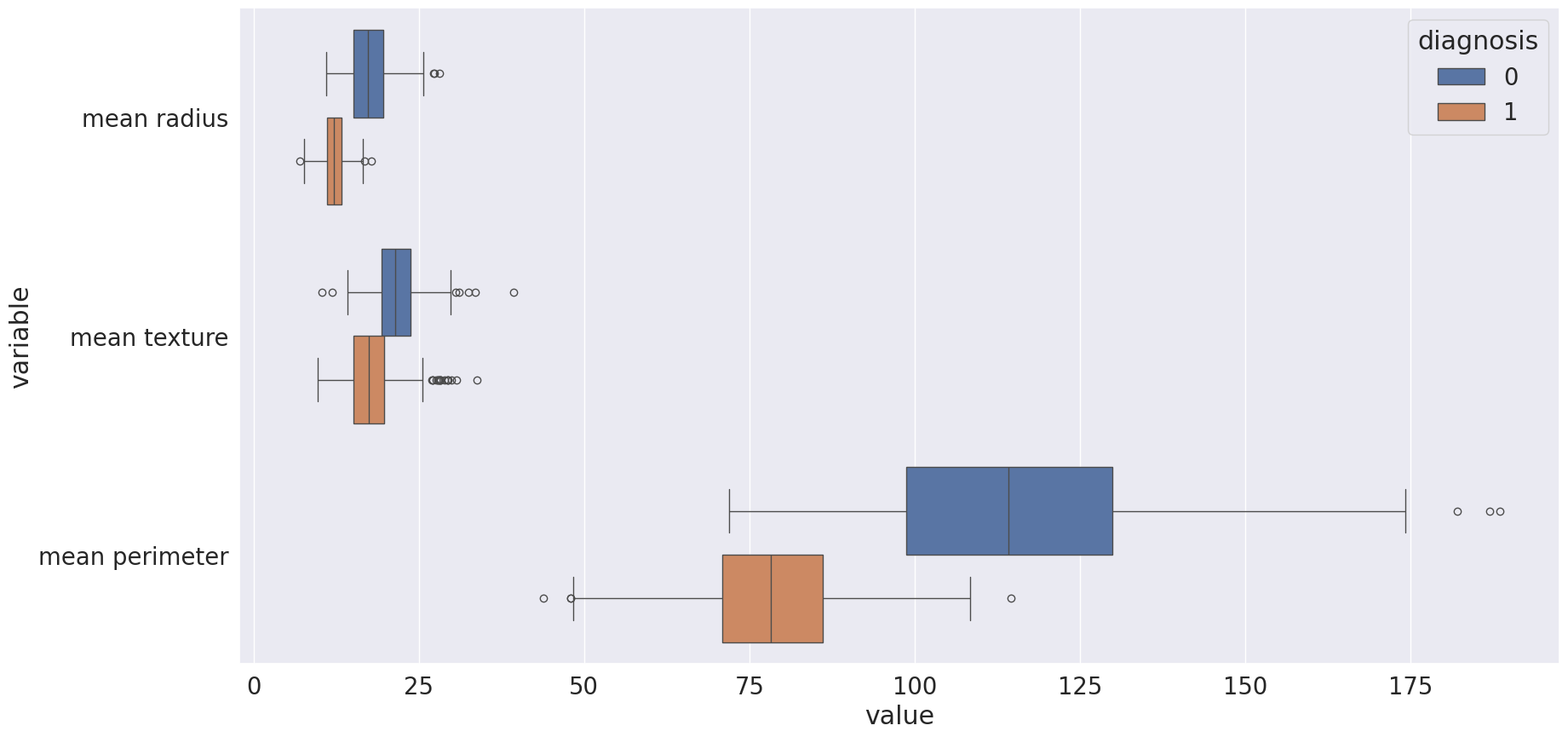
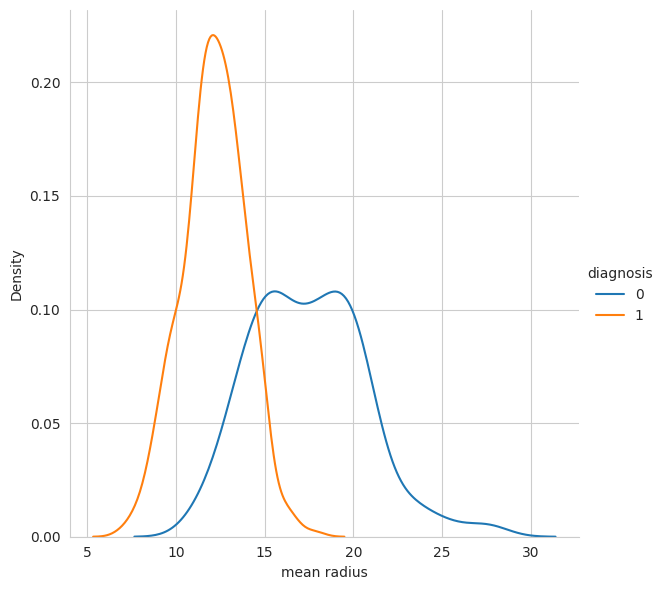
Diagrama de densidad de distribución KDE y distribución mediante el diagrama de dispersión
stripplot()
matplotlib.rc_file_defaults()
sns.set_style("whitegrid")
sns.FacetGrid(df, hue="diagnosis", height=6).map(sns.kdeplot, "mean radius").add_legend();
sns.stripplot(x="diagnosis", y="mean radius", data=df, jitter=True, edgecolor="gray");
¿Debo siempre eliminar variables explicativas no correlacionadas con mi variable respuesta?
No es obligatorio eliminar variables sin correlación con la variable respuesta. La correlación mide solo relaciones lineales, y algunas variables pueden ser útiles en modelos no lineales. Además, algoritmos como Lasso, Random Forest o Gradient Boosting, SVM, ANNs manejan variables irrelevantes automáticamente.
Eliminar prematuramente puede descartar información valiosa. Sin embargo, un análisis de importancia de características sigue siendo recomendable para mejorar eficiencia y evitar ruido innecesario. En su lugar, es mejor aplicar técnicas como SHAP, Permutation Importance, RFE o transformaciones como PCA para evaluar la relevancia de las variables antes de eliminarlas.
2.6.1. Multicolinealidad#
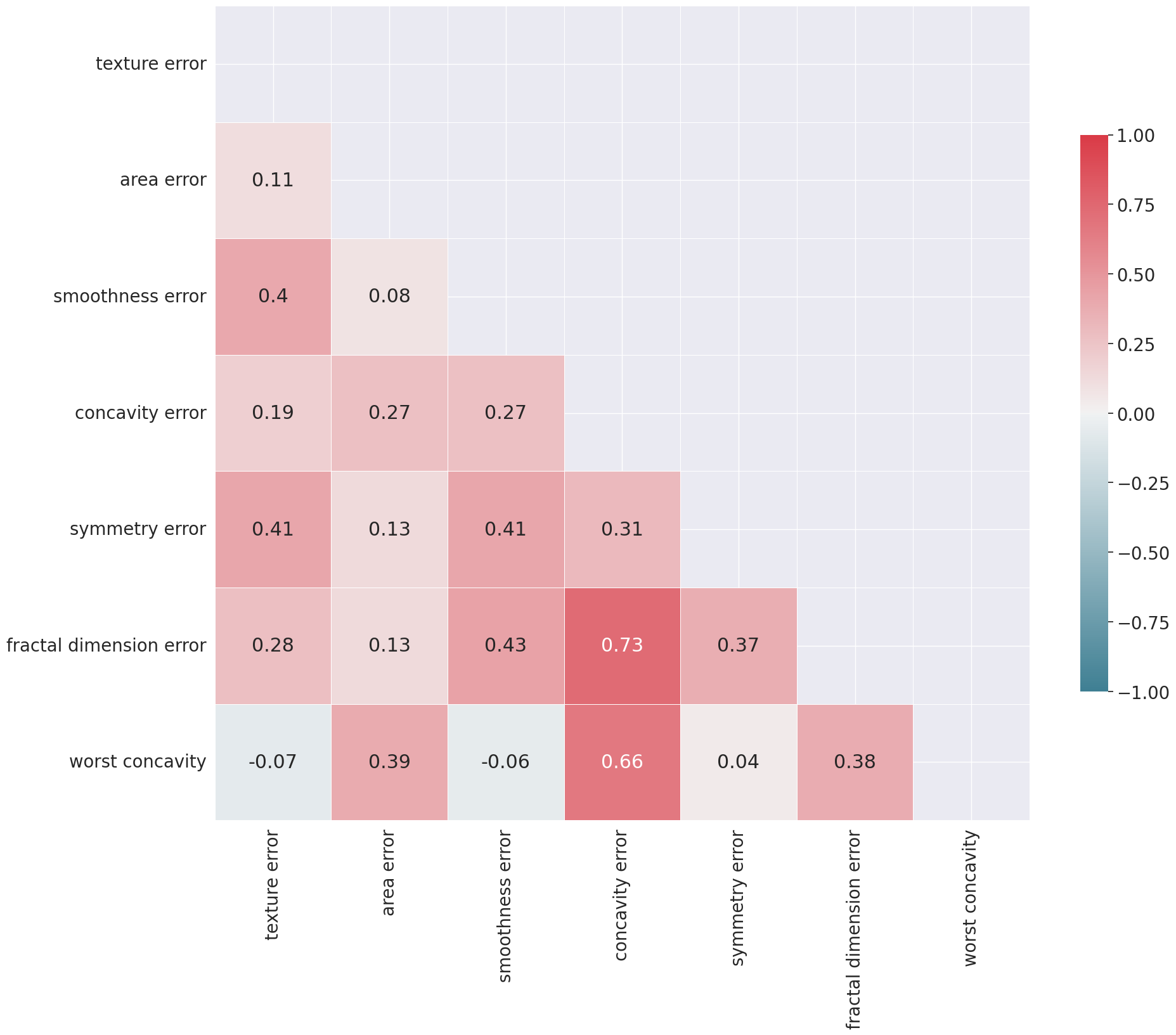
La multicolinealidad es un problema ya que, reduce la importancia de las variables independientes. A fin de solucionar este problema, se eliminan los predictores altamente correlacionados. Podemos comprobar la presencia de multicolinealidad entre algunas de las variables. Por ejemplo, la columna mean radius tiene una correlación de 1.0 con las columnas mean perimeter y mean área, respectivamente. Esto se debe a que las tres columnas contienen esencialmente la misma información, que es el tamaño físico de la observación.
Por lo tanto, sólo debemos elegir una de las tres columnas cuando pasemos al análisis posterior. Otro lugar donde la multicolinealidad es evidente, es entre las columnas
"mean"y"worst". Por ejemplo, la columnamean radiustiene una correlación de 1.0 con la columnaworst radius. También hay multicolinealidad entre los atributoscompactness, concavityyconcave points. Así que podemos elegir solo uno de estos, por ejemplocompactness. De la matriz de correlación sabemos que estas columnas están altamente correlacionadas con las columnasmean radius,perimeter,area.
2.6.2. Factor de Inflación de la Varianza (VIF)#
Para abordar la multicolinealidad, se pueden aplicar técnicas como la regularización o la selección de características para, seleccionar un subconjunto de variables independientes que no estén altamente correlacionadas entre sí. En esta sección, nos centraremos en la más común: VIF (Factores de Inflación de la Varianza).
El
VIFdetermina la fuerza de la correlación entre las variables independientes. Se pronostica tomando una variable y comparándola con todas las demás. La puntuaciónVIFde una variable independiente representa hasta qué punto la variable se explica por otras variables independientes.El valor \(R^2\) se determina para averiguar hasta qué punto una variable independiente es descrita por las demás variables independientes. Un valor alto de \(R^{2}\) significa que la variable está muy correlacionada con las demás variables. Esto se refleja en el
VIF, que se indica a continuación:
Así, cuanto más se acerque el valor de \(R^2\) a 1, mayor será el valor de
VIFy mayor la multicolinealidad con la variable independiente concreta.
Observación
Un valor VIF de 1: Sin multicolinealidad (variable perfectamente independiente).
Un valor VIF entre 1 y 5: Multicolinealidad baja a moderada (no se considera problemática).
Un valor VIF entre 5 y 10: Multicolinealidad moderada a alta (considerada problemática).
Un valor VIF superior a 10: Multicolinealidad alta (preocupación grave, requiere medidas).
from statsmodels.stats.outliers_influence import variance_inflation_factor
def VIF_calculation(X):
VIF = pd.DataFrame()
VIF["variable"] = X.columns
VIF["VIF"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
VIF = VIF.sort_values('VIF', ascending=False).reset_index(drop = True)
return(VIF)
def delete_multicollinearity(df, target_name, VIF_threshold):
X = df.drop(target_name, axis=1)
VIF_mat = VIF_calculation(X)
n_VIF = VIF_mat["VIF"][0]
if (n_VIF <= VIF_threshold):
print("There is no multicollinearity!")
else:
while (n_VIF > VIF_threshold):
X = X.drop(VIF_mat["variable"][0], axis=1)
VIF_mat = VIF_calculation(X)
n_VIF = VIF_mat["VIF"][0]
display(VIF_mat)
return X
df_copy = delete_multicollinearity(df_copy, "diagnosis", 10)
| variable | VIF | |
|---|---|---|
| 0 | symmetry error | 8.648328 |
| 1 | smoothness error | 8.347757 |
| 2 | fractal dimension error | 7.644681 |
| 3 | texture error | 7.103564 |
| 4 | concavity error | 6.666504 |
| 5 | worst concavity | 4.620458 |
| 6 | area error | 2.190762 |
df_copy.head()
| texture error | area error | smoothness error | concavity error | symmetry error | fractal dimension error | worst concavity | |
|---|---|---|---|---|---|---|---|
| 0 | 0.9053 | 153.40 | 0.006399 | 0.05373 | 0.03003 | 0.006193 | 0.7119 |
| 1 | 0.7339 | 74.08 | 0.005225 | 0.01860 | 0.01389 | 0.003532 | 0.2416 |
| 2 | 0.7869 | 94.03 | 0.006150 | 0.03832 | 0.02250 | 0.004571 | 0.4504 |
| 3 | 1.1560 | 27.23 | 0.009110 | 0.05661 | 0.05963 | 0.009208 | 0.6869 |
| 4 | 0.7813 | 94.44 | 0.011490 | 0.05688 | 0.01756 | 0.005115 | 0.4000 |
corr = df_copy.corr().round(2)
cmap = sns.diverging_palette(220, 10, as_cmap=True)
mask = np.zeros_like(corr)
mask[np.triu_indices_from(mask)] = True
sns.set(font_scale=1.8)
f, ax = plt.subplots(figsize=(20, 20))
sns.heatmap(corr, mask=mask, cmap=cmap, vmin=-1, vmax=1, center=0, square=True, linewidths=.5,
cbar_kws={"shrink": .5}, annot=True)
plt.tight_layout()
¿Debo siempre eliminar variables que presentan multicolinealidad?
La multicolinealidad afecta modelos lineales e interpretativos, pero no es un problema en modelos más complejos
Debe eliminarse (afecta estabilidad e interpretación):
Regresión Lineal y Logística → Inestabilidad en coeficientes, detectada con VIF.
Linear Discriminant Analysis (LDA) → Depende de matrices de covarianza, afectadas por multicolinealidad.
Ridge y Lasso → Ridge la mitiga, Lasso selecciona algunas variables.
No es un problema grave (modelos robustos):
Árboles de Decisión (Random Forest, XGBoost) → Seleccionan variables jerárquicamente.
SVM (kernels no lineales) → Puede aumentar costo computacional, pero no afecta resultados.
Redes Neuronales → No dependen de relaciones lineales, pero pueden sobreajustar con muchas variables redundantes.
KNN → No usa coeficientes, multicolinealidad irrelevante.
2.7. Selección del modelo K-NN#
División en entrenamiento (train) y prueba (test). Dividimos la variable objetivo y las variables independientes. A continuación, evaluamos el rendimiento del conjunto de entrenamiento y de prueba con diferentes números de vecinos
from sklearn.model_selection import train_test_split
Utilizaremos en el presente problema las columnas obtenidas luego de aplicar el Factor de Inflación de la Varianza (VIF). Pude verificar que sucede cuando utiliza el dataset inicial, en el cual se retiraron de manera manual varias características, con base en la matriz de correlación
X = df_copy
y = df['diagnosis']
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=cancer.target, random_state=66)
training_accuracy = []
test_accuracy = []
neighbors_settings = range(1, 20)
for n_neighbors in neighbors_settings:
clf = KNeighborsClassifier(n_neighbors=n_neighbors)
clf.fit(X_train, y_train)
training_accuracy.append(clf.score(X_train, y_train))
test_accuracy.append(clf.score(X_test, y_test))
matplotlib.rc_file_defaults()
plt.plot(neighbors_settings, training_accuracy, label="Training accuracy")
plt.plot(neighbors_settings, test_accuracy, label="Test accuracy")
plt.ylabel("Accuracy")
plt.xlabel("n_neighbors")
plt.legend();
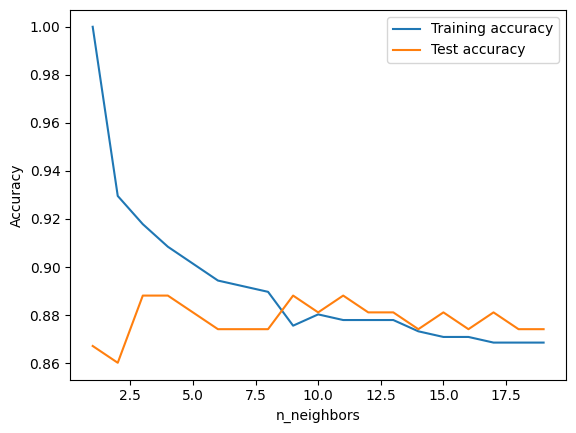
El gráfico muestra accuracy para los conjuntos de entrenamiento y de prueba en el eje \(y\) contra el ajuste de
n_vecinosen el eje \(x\). Aunque los gráficos del mundo real no suelen ser muy suaves, podemos reconocer algunas de las características del sobreajuste (overfitting) y del subajuste (underfitting). Si se considera un solo vecino más cercano, la predicción en el conjunto de entrenamiento es perfecta. Pero cuando se consideran más vecinos, el modelo se simplifica y la precisión del entrenamiento disminuye.La precisión del conjunto de prueba cuando se utiliza un solo vecino es menor que cuando se utilizan más vecinos, lo que indica que el uso de un solo vecino más cercano conduce a una mayor precisión en el conjunto de entrenamiento (modelo demasiado complejo). Pero cuando se consideran más vecinos, el modelo se simplifica y la precisión del entrenamiento disminuye.
clf = KNeighborsClassifier(n_neighbors=9)
clf.fit(X_train, y_train)
KNeighborsClassifier(n_neighbors=9)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
KNeighborsClassifier(n_neighbors=9)
print(clf.score(X_train, y_train), clf.score(X_test, y_test))
0.8755868544600939 0.8881118881118881
Queda como ejercicio para el lector aplicar las técnicas de validación cruzada y grid search para obtener el mejor modelo \(k\)-NN para este problema de aplicación.
from sklearn.model_selection import cross_val_score
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_breast_cancer
import numpy as np
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, stratify=cancer.target, random_state=10)
best_score = 0
for n_neighbors in range(1, 20):
knn = KNeighborsClassifier(n_neighbors=n_neighbors)
scores = cross_val_score(knn, X_train, y_train, cv=5)
score = np.mean(scores)
if score > best_score:
best_score = score
best_parameters = {'n_neighbors': n_neighbors}
print("Best cross-validation accuracy: {:.2f}".format(best_score))
print("Best parameters: ", best_parameters)
Best cross-validation accuracy: 0.94
Best parameters: {'n_neighbors': 5}
knn = KNeighborsClassifier(**best_parameters)
knn.fit(X_train, y_train)
KNeighborsClassifier()In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
KNeighborsClassifier()
print("Train set accuracy:", knn.score(X_train, y_train), "; Test set accuracy:", knn.score(X_test, y_test))
Train set accuracy: 0.9460093896713615 ; Test set accuracy: 0.9230769230769231
2.8. Regresión por \(k\)-vecinos#
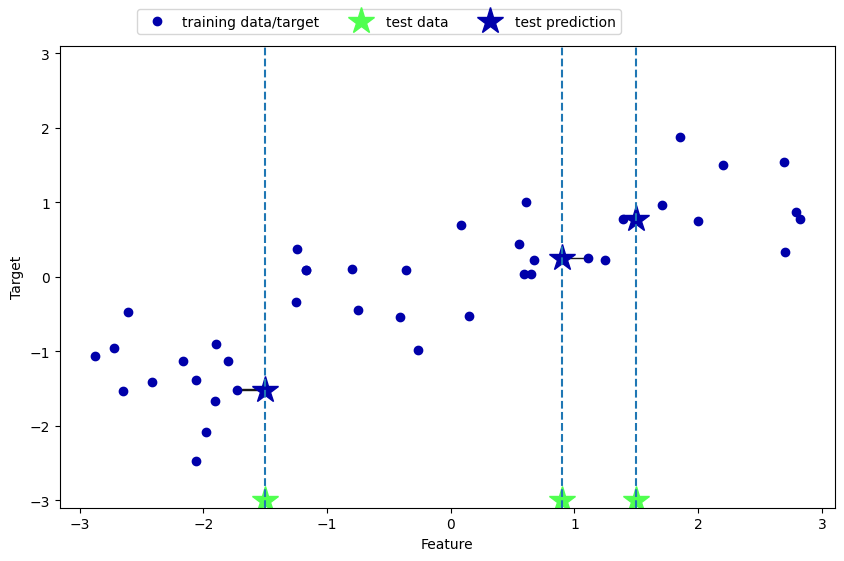
También existe una variante de regresión del algoritmo \(k\)-vecinos más cercanos. Una vez más, vamos a empezar utilizando el vecino más cercano simple, esta vez utilizando el conjunto de datos
wave. Hemos añadido tres puntos de datos de prueba como estrellas verdes en el eje \(x\). La predicción utilizando un solo vecino es sólo el valor objetivo del vecino más cercano
mglearn.plots.plot_knn_regression(n_neighbors=1)
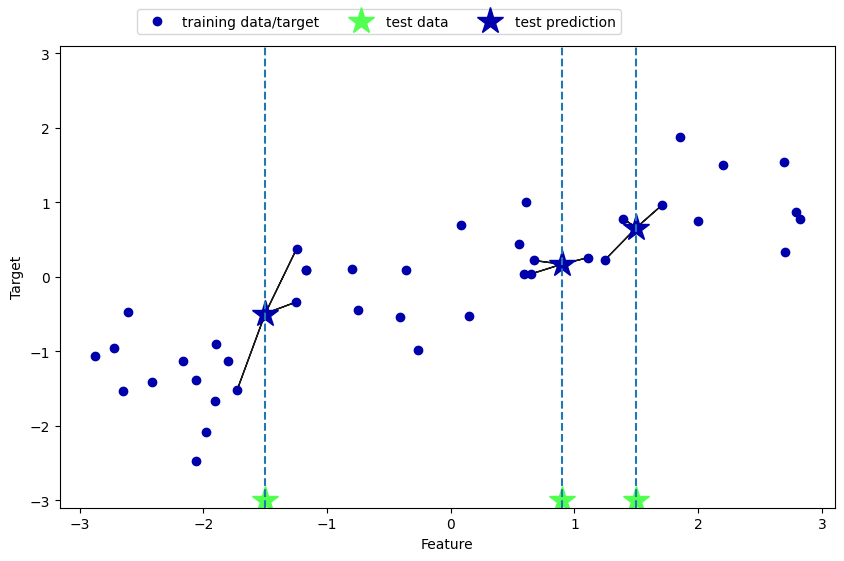
De nuevo, podemos utilizar más que el único vecino más cercano para la regresión. Cuando se utilizan varios vecinos más cercanos, la predicción es el promedio, o la media, de los vecinos
mglearn.plots.plot_knn_regression(n_neighbors=3)
El algoritmo de \(k\)-vecinos más cercanos para la regresión se implementa en la clase
KNeighbors Regressorenscikit-learn. Se utiliza de forma similar aKNeighborsClassifier
from sklearn.neighbors import KNeighborsRegressor
X, y = mglearn.datasets.make_wave(n_samples=40)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
reg = KNeighborsRegressor(n_neighbors=3)
reg.fit(X_train, y_train)
KNeighborsRegressor(n_neighbors=3)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
KNeighborsRegressor(n_neighbors=3)
Ahora podemos hacer predicciones sobre el conjunto de prueba
print("Test set predictions:\n{}".format(reg.predict(X_test)))
Test set predictions:
[-0.05396539 0.35686046 1.13671923 -1.89415682 -1.13881398 -1.63113382
0.35686046 0.91241374 -0.44680446 -1.13881398]
También podemos evaluar el modelo utilizando el método score, que para los regresores devuelve la puntuación \(R^2\). La puntuación \(R^2\), también conocida como coeficiente de determinación, es una medida de predicción de un modelo de regresión, y arroja una puntuación entre 0 y 1. Un valor de 1 corresponde a una predicción perfecta, y un valor de 0 corresponde a un modelo constante que sólo predice la media de las respuestas del conjunto de entrenamiento,
y_train. Aquí, elscorees de 0.83, lo que indica un ajuste del modelo relativamente bueno.
print("Test set R^2: {:.2f}".format(reg.score(X_test, y_test)))
Test set R^2: 0.83
2.9. Análisis de KNeighborsRegressor#
Para nuestro conjunto de datos unidimensional, podemos ver cómo son las predicciones para todos los valores posibles de las características. Para ello, creamos un conjunto de datos de prueba compuesto por muchos puntos de la línea
import numpy as np
fig, axes = plt.subplots(1, 3, figsize=(15, 4))
line = np.linspace(-3, 3, 1000).reshape(-1, 1)
for n_neighbors, ax in zip([1, 3, 9], axes):
reg = KNeighborsRegressor(n_neighbors=n_neighbors)
reg.fit(X_train, y_train)
ax.plot(line, reg.predict(line))
ax.plot(X_train, y_train, '^', c=mglearn.cm2(0), markersize=8)
ax.plot(X_test, y_test, 'v', c=mglearn.cm2(1), markersize=8)
ax.set_title("{} neighbor(s)\n train score: {:.2f} test score: {:.2f}".format(n_neighbors,
reg.score(X_train, y_train),
reg.score(X_test, y_test)))
ax.set_xlabel("Feature")
ax.set_ylabel("Target")
axes[0].legend(["Model predictions", "Training data/target", "Test data/target"], loc="best");
Como podemos ver en el gráfico, al utilizar un solo vecino, cada punto del conjunto de entrenamiento tiene una influencia obvia en las predicciones, y los valores predichos pasan por todos los puntos de datos. Esto conduce a una predicción muy inestable. Tener en cuenta más vecinos conduce a predicciones más suaves, pero éstas no se ajustan tan bien a los datos de entrenamiento.
2.9.1. Aplicación: World Hydropower Generation#
World Hydropower Generation: Esta sección se centra en el uso del modelo \(k\)-NN y sus hiperparamétros, para garantizar una mejor comprensión de este algoritmo. No se utilizan otros recursos como la ingeniería de características, la reducción de dimensionalidad. El conjunto de datos utilizado es una recopilación de la generación de energía de varios países europeos, medida en THh entre 2000 y 2019. Su contenido fue extraído de World in Data.
En primer lugar, se importan las librerías básicas:
pandas, matplotlibynumpyparaDataframes, Gráficosy operaciones numéricas;MinMaxScalerpara normalizar nuestros datos entre 0 y 1,train_test_splitpara ayudar a dividir el conjunto de datos (normalmente 70% entrenamiento/ 30% prueba) yneighborspara generar nuestros modelos usando kNN
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
from sklearn import neighbors
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_squared_log_error
from sklearn.metrics import r2_score
from sklearn.metrics import explained_variance_score
Para medir la eficacia de nuestros modelos generados, utilizamoslas siguientes métricas:
mean_absolute_error (MAE): medida de los errores entre observaciones emparejadas que expresan el mismo fenómeno; \(\text{MAE}=\frac{1}{n}\sum_{j=1}^{n}|y_{j}-\hat{y}_{j}|\)
mean_squared_error (root - RMSE): la desviación estándar de los residuos (errores de predicción); \(\text{RMSE}=\sqrt{\frac{1}{n}\sum_{j=1}^{n}(y_{j}-\hat{y}_{j})^{2}}\)
mean_squared_log_error (root - RMSLE): mide la relación entre lo real y lo predicho; \(\text{RMSLE}=\sqrt{\frac{1}{n}\sum_{j=1}^{n}(\log(y_{j}+1)-\log(\hat{y}_{j}+1))^{2}}\)
r2_score (R2):: coeficiente de determinación, la proporción de la varianza en la variable dependiente que es predecible a partir de la(s) variable(s) independiente(s); \(R^{2}=1-\sum_{j=1}^{n}(y_{j}-\hat{y}_{j})^{2}/\sum_{j=1}^{n}(y_{j}-\overline{y}_{j})^{2}\)
explained_variance_score (EVS): mide la discrepancia entre un modelo y los datos reales \(\text{EVS}=1-\text{Var}(y-\hat{y})/\text{Var}(y).\)
Preprocesamiento de datos: Inicialmente, los datos son importados, y se excluyen las columnas categóricas (en este caso, sólo"Country"). Para transformar el conjunto de datos y mantenerlo como unDataframe, se utiliza la libreríascalerdentro de la librería Dataframe, normalizando los datos entre 0 y 1, y manteniendo las propiedades del dataframe. Después de esto, se llama a la funcióndescribe, para mostrar algunos datos importantes sobre eldataframe, comomean, max, min, stdy otros.
pd.options.display.float_format = '{:.4f}'.format
scaler = MinMaxScaler(feature_range=(0, 1))
df_power = pd.read_csv('https://raw.githubusercontent.com/lihkir/Data/main/Hydropower_Consumption.csv', sep=',')
df_power.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 153 entries, 0 to 152
Data columns (total 21 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Country 153 non-null object
1 2000 153 non-null int64
2 2001 153 non-null int64
3 2002 153 non-null int64
4 2003 153 non-null int64
5 2004 153 non-null int64
6 2005 153 non-null int64
7 2006 153 non-null int64
8 2007 153 non-null int64
9 2008 153 non-null int64
10 2009 153 non-null int64
11 2010 153 non-null int64
12 2011 153 non-null int64
13 2012 153 non-null int64
14 2013 153 non-null int64
15 2014 153 non-null int64
16 2015 153 non-null int64
17 2016 153 non-null int64
18 2017 153 non-null int64
19 2018 153 non-null int64
20 2019 153 non-null int64
dtypes: int64(20), object(1)
memory usage: 25.2+ KB
df_power.head()
| Country | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | ... | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Afghanistan | 312 | 498 | 555 | 63 | 565 | 59 | 637 | 748 | 542 | ... | 751 | 595 | 71 | 804 | 895 | 989 | 1025 | 105 | 105 | 107 |
| 1 | Africa | 75246 | 80864 | 85181 | 82873 | 87405 | 89066 | 92241 | 95341 | 97157 | ... | 107427 | 110445 | 110952 | 117673 | 123727 | 115801 | 123816 | 130388 | 132735 | 0 |
| 2 | Albania | 4548 | 3519 | 3477 | 5117 | 5411 | 5319 | 4951 | 276 | 3759 | ... | 7673 | 4036 | 4725 | 6959 | 4726 | 5866 | 7136 | 448 | 448 | 4018 |
| 3 | Algeria | 54 | 69 | 57 | 265 | 251 | 555 | 218 | 226 | 283 | ... | 173 | 378 | 389 | 99 | 193 | 145 | 72 | 56 | 117 | 152 |
| 4 | Angola | 903 | 1007 | 1132 | 1229 | 1733 | 2197 | 2638 | 2472 | 3103 | ... | 3666 | 3967 | 3734 | 4719 | 4991 | 5037 | 5757 | 7576 | 7576 | 8422 |
5 rows × 21 columns
countries = df_power.Country
df_power = df_power.drop(columns = ["Country"])
df_power = pd.DataFrame(scaler.fit_transform(df_power),
columns=['2000','2001','2002','2003','2004','2005',
'2006','2007','2008','2009','2010','2011',
'2012','2013','2014','2015','2016','2017',
'2018','2019'])
df_power.describe()
| 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 153.0000 | 153.0000 | 153.0000 | 153.0000 | 153.0000 | 153.0000 | 153.0000 | 153.0000 | 153.0000 | 153.0000 | 153.0000 | 153.0000 | 153.0000 | 153.0000 | 153.0000 | 153.0000 | 153.0000 | 153.0000 | 153.0000 | 153.0000 |
| mean | 0.0327 | 0.0353 | 0.0355 | 0.0328 | 0.0419 | 0.0390 | 0.0415 | 0.0434 | 0.0371 | 0.0445 | 0.0328 | 0.0433 | 0.0352 | 0.0290 | 0.0282 | 0.0265 | 0.0306 | 0.0296 | 0.0388 | 0.0259 |
| std | 0.1229 | 0.1262 | 0.1278 | 0.1249 | 0.1372 | 0.1364 | 0.1366 | 0.1440 | 0.1293 | 0.1493 | 0.1208 | 0.1459 | 0.1294 | 0.1121 | 0.1062 | 0.1031 | 0.1117 | 0.1110 | 0.1317 | 0.1043 |
| min | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 25% | 0.0002 | 0.0003 | 0.0003 | 0.0003 | 0.0003 | 0.0004 | 0.0003 | 0.0004 | 0.0004 | 0.0003 | 0.0004 | 0.0002 | 0.0004 | 0.0002 | 0.0003 | 0.0002 | 0.0002 | 0.0002 | 0.0003 | 0.0002 |
| 50% | 0.0027 | 0.0030 | 0.0026 | 0.0027 | 0.0037 | 0.0028 | 0.0031 | 0.0039 | 0.0032 | 0.0035 | 0.0043 | 0.0040 | 0.0034 | 0.0025 | 0.0024 | 0.0019 | 0.0025 | 0.0020 | 0.0029 | 0.0019 |
| 75% | 0.0116 | 0.0128 | 0.0119 | 0.0118 | 0.0155 | 0.0107 | 0.0149 | 0.0151 | 0.0147 | 0.0152 | 0.0145 | 0.0156 | 0.0140 | 0.0096 | 0.0121 | 0.0086 | 0.0117 | 0.0113 | 0.0171 | 0.0097 |
| max | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
Ahora, el objetivo es crear un modelo que prediga la generación de energía para 2019, basándose en los 18 años anteriores (2000 - 2018) con al menos un 75% de precisión. Para ello, el conjunto de datos se separó en
Xey, siendoXdatos de predicción eylo que se pretende predecir. Para ello, se dividen en entrenamiento (70%) y prueba (30%).
X = df_power.drop(columns = ["2019"])
y = df_power["2019"]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
Como ya tenemos seleccionados los datos de entrenamiento y de prueba, es necesario encontrar el factor \(k\) que genere los mejores resultados para el algoritmo. Una de las formas de encontrar este factor \(k\) es realizar una prueba con varios valores y medir los resultados porcentuales. Será necesario agotar un gran número de posibilidades de \(k\)
rmsle_val = []
best_rmsle = 1.0
for k in range(20):
k = k+1
knn = neighbors.KNeighborsRegressor(n_neighbors = k)
knn.fit(X_train, y_train)
y_pred = knn.predict(X_test)
rmsle = np.sqrt(mean_squared_log_error(y_test,y_pred))
if (rmsle < best_rmsle):
best_rmsle = rmsle
best_k = k
rmsle_val.append(rmsle)
print('RMSLE value for k= ' , k , 'is:', rmsle)
print(f"Best RMSLE: {best_rmsle}, Best k: {best_k}")
RMSLE value for k= 1 is: 0.05771085849033799
RMSLE value for k= 2 is: 0.046287824938614094
RMSLE value for k= 3 is: 0.05245290672301628
RMSLE value for k= 4 is: 0.039043708745309796
RMSLE value for k= 5 is: 0.04413545109970342
RMSLE value for k= 6 is: 0.049397885066996064
RMSLE value for k= 7 is: 0.05368842644105438
RMSLE value for k= 8 is: 0.057205532019402504
RMSLE value for k= 9 is: 0.05970971610365409
RMSLE value for k= 10 is: 0.06264220706736036
RMSLE value for k= 11 is: 0.06519555508343818
RMSLE value for k= 12 is: 0.06683376633168203
RMSLE value for k= 13 is: 0.06835697276199447
RMSLE value for k= 14 is: 0.07009875902703569
RMSLE value for k= 15 is: 0.0714815908074978
RMSLE value for k= 16 is: 0.07276108145829546
RMSLE value for k= 17 is: 0.07381745094856672
RMSLE value for k= 18 is: 0.07488933459172763
RMSLE value for k= 19 is: 0.07579673979403485
RMSLE value for k= 20 is: 0.07667076282857414
Best RMSLE: 0.039043708745309796, Best k: 4
Nuestra métrica indica que el menor error se produce cuando tenemos \(k = 4\) (RMSLE de 0.0390), lo que indica un error relativo entre los valores predichos y los actuales del 3,90%. Por lo tanto, presentaremos todos los valores en un gráfico, que nos mostrará visualmente los resultados obtenidos. Esta función se conoce como “función codo”, dada la variación porcentual que se produce entre los valores de \(k\), primero hacia abajo y luego hacia arriba, cuando \(k\) encuentra su mejor valor. Estamos trazando los valores RMSLE frente a los valores de \(k\).
curve = pd.DataFrame(rmsle_val)
curve.plot(figsize=(8,5));
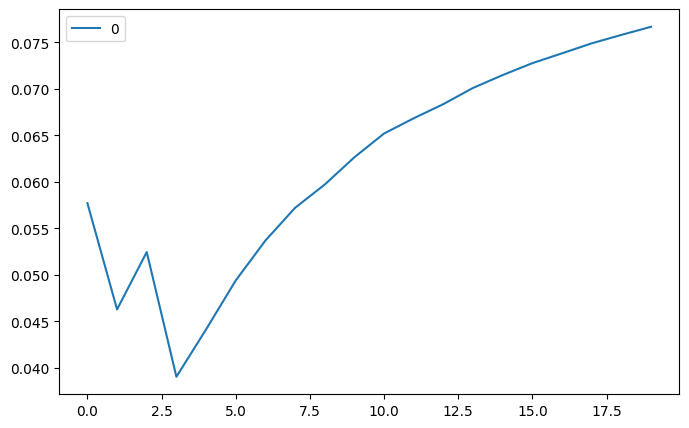
El gráfico muestra una caída brusca del RMSLE a medida que \(k\) avanza hasta 4, momento en el que empieza a aumentar indefinidamente, lo que nos lleva a la conclusión de que 4 es el mejor resultado para \(k\). Una vez encontrado el mejor valor para \(k\), es hora de entrenar el modelo y predecir los resultados. También haremos uso de la función de `score***, que nos permitirá ver la tasa de precisión de nuestro modelo (80,16%).
knn = neighbors.KNeighborsRegressor(n_neighbors = 4)
knn.fit(X_train,y_train)
y_pred = knn.predict(X_test)
knn.score(X_test, y_test)
0.8016285342188538
Una vez se ha construido el modelo y se prueban algunas predicciones, podemos aplicar las métricas y analizar los resultados. Aquí se comparan el conjunto de prueba con las predicciones usando las métricas
R2, EVS, MAE, RMSE, RMSLE, para verificar cuáles son los resultados de cada una de ellas.
r2_valid = r2_score(y_test, y_pred)
mae_valid = mean_absolute_error(y_test, y_pred)
evs_valid = explained_variance_score(y_test, y_pred, multioutput='uniform_average')
rmse_valid = np.sqrt(mean_squared_error(y_test, y_pred))
rmsle_valid = np.sqrt(mean_squared_log_error(y_test, y_pred))
print('R2 Valid:',r2_valid)
print('EVS Valid:', evs_valid)
print('MAE Valid:', mae_valid)
print('RMSE Valid:',rmse_valid)
print('RMSLE Valid:', rmsle_valid)
R2 Valid: 0.8016285342188538
EVS Valid: 0.8131526313306373
MAE Valid: 0.017960057840249434
RMSE Valid: 0.04999229884993785
RMSLE Valid: 0.039043708745309796
Los resultados muestran un
R2 del 80,16%y unEVS del 81,31%, lo que indica que nuestro modelo tiene un gran ajuste a su muestra (R2) y una fuerte asociación entre el modelo y sus datos actuales (EVS). En cuanto al RMSLE, sólo tiene en cuenta el error relativo entre el valor previsto y el real, y la escala del error no es significativa. Por otro lado, el valor RMSE aumenta en magnitud si aumenta la escala del error.
Una vez realizada la predicción y comprobado el modelo, organizamos los resultados uno al lado del otro para poder hacer una comparación.
country_test = countries[len(countries)-len(y_test):]
data_prediction = list(zip(y_test,y_pred))
data_prediction = pd.DataFrame(data_prediction, columns=['Test','Prediction'])
data_prediction = data_prediction.set_index(country_test)
data_prediction.head(10)
| Test | Prediction | |
|---|---|---|
| Country | ||
| Papua New Guinea | 0.0406 | 0.0268 |
| Paraguay | 0.0044 | 0.0039 |
| Peru | 0.0134 | 0.0096 |
| Phillipines | 0.0280 | 0.0128 |
| Poland | 0.0164 | 0.0125 |
| Portugal | 0.0321 | 0.0155 |
| Puerto Rico | 0.4982 | 0.3417 |
| Reunion | 0.5331 | 0.3417 |
| Romania | 0.0007 | 0.0075 |
| Russia | 0.0032 | 0.0039 |
plt.rcParams.update({'font.size': 18});
plt.figure(figsize=(20, 8));
plt.plot(data_prediction.index, data_prediction.Test, label="Test");
plt.plot(data_prediction.index, data_prediction.Prediction, label="Prediction");
plt.xticks(rotation=90);
plt.legend(loc="upper right");
plt.xlabel("Country");
plt.ylabel("Hydropower Generation");
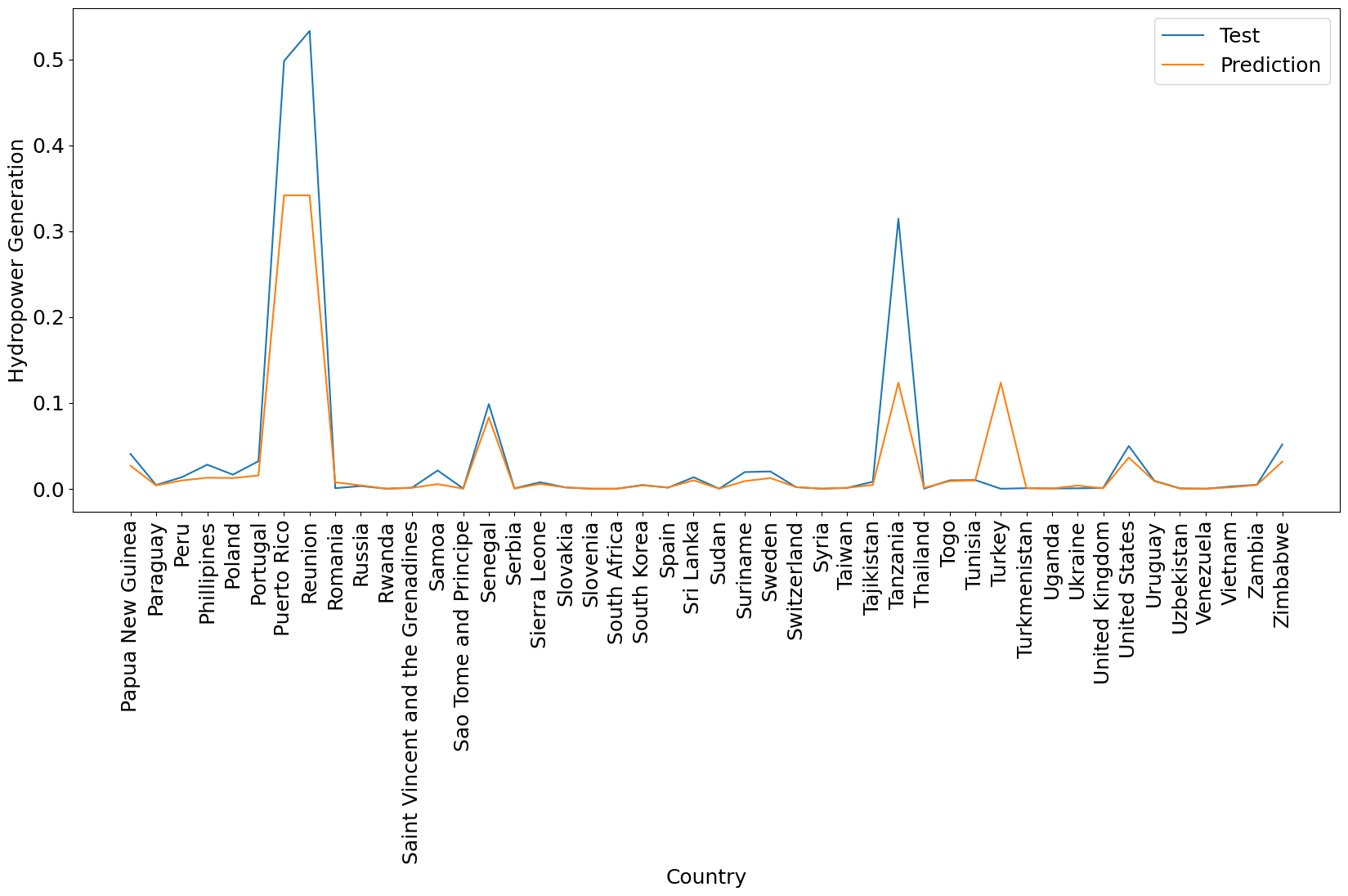
Nótese que el conjunto de prueba para este ejemplo fue tomado como, el último 30% de nuestras observaciones, lo cual corresponde a los últimos 46 países (observaciones) existentes en nuestro dataset. En la sección dedicada a la evaluación de modelos, se abordarán técnicas especificas para que pliegues de prueba sean repartidos proporcionalmente en todas las posiciones posibles en nuestro data set, usando la librería
KFold, así como también hiperparametrización usandoGridSearch.
Puntos fuertes, puntos débiles y parámetros
En principio, hay dos parámetros importantes en el clasificador
KNeighbors: el número de vecinos y cómo se mide la distancia entre los puntos de datos. En la práctica, utilizar un número pequeño de vecinos, como tres o cinco, suele funcionar bien, pero se debería ajustar este parámetro.La elección de la medida de distancia correcta es también crucial. Por defecto,
KNeighborsutiliza la distancia euclidiana, que funciona bien en muchos casos. Uno de los puntos fuertes de \(k\)-NN es que el modelo es muy fácil de entender, y a menudo da un rendimiento razonable sin necesidad de muchos ajustes. El uso de este algoritmo es un buen método de referencia para probar, antes de considerar técnicas más avanzadas.La construcción del modelo de vecinos más cercanos suele ser muy rápida, pero cuando el conjunto de entrenamiento es muy grande (ya sea en número de características o en número de muestras) la predicción puede ser lenta. Cuando se utiliza el algoritmo \(k\)-NN, es importante pre-procesar los datos, tema que revisaremos en secciones posteriores. Este enfoque no suele funcionar bien en conjuntos de datos con muchas características (cientos o más), y lo hace especialmente mal con conjuntos de datos en los que la mayoría de las características son 0 la mayor parte del tiempo (los llamados conjuntos de datos dispersos).
Por lo tanto, aunque el algoritmo de \(k\)-vecinos más cercanos es fácil de entender, no se utiliza a menudo en la práctica, debido a que la predicción es lenta y a su incapacidad para manejar muchas características.