Clasificador Bayesiano

4. Clasificador Bayesiano#

Observación

Naive Bayes es una familia de clasificadores similares a los modelos lineales, pero más rápidos en entrenamiento, aunque con menor rendimiento de generalización que LogisticRegression y LinearSVC.
Son eficientes porque aprenden los parámetros observando cada característica individualmente. scikit-learn ofrece tres variantes:
- GaussianNB asume que las variables explicativas siguen una distribución normal.
- BernoulliNB se usa cuando las variables explicativas son binarias (0 o 1).
- MultinomialNB se aplica cuando las variables explicativas representan conteos enteros (como frecuencia de palabras en texto).
En BernoulliNB, “frecuencia de características distintas de cero” significa que se considera cuántas veces una característica binaria es 1 en cada clase.

4.1. Formulación#

En la clasificación mediante el enfoque Bayesiano, el concepto básico está plasmado en el Teorema de Bayes. Como ejemplo, supongamos que hemos observado la aparición de un síntoma en un determinado paciente en forma de fiebre y necesitamos evaluar si ha sido causado por un resfriado o por la inﬂuenza. Si la probabilidad de que un resfriado sea la causa de la fiebre es mayor que la de la inﬂuenza, entonces podemos atribuir, al menos tentativamente, la fiebre de este paciente a un resfriado.

Este es el concepto subyacente de la clasificación de Bayes. El Teorema de Bayes da la relación entre la probabilidad condicional de un evento basado en la información adquirida, que en este caso puede describirse de la siguiente manera

En primer lugar, denotamos la probabilidad de fiebre (\(D\)) como síntoma de un resfriado (\(G1\) ) y de la inﬂuenza (\(G2\)) por

\[ P(D|G_{1})=\frac{P(D\cap G_{1})}{P(G_{1})},\quad P(D|G_{2})=\frac{P(D\cap G_{2})}{P(G_{2})}, \]

respectivamente. \(P(D|G_{1})\) y \(P(D|G_{2})\) representan las probabilidades de que la fiebre sea el resultado de un resfriado y de la inﬂuenza, respectivamente, y se denominan probabilidades condicionales. Aquí, \(P(G_{1})\) y \(P(G_{2})\) \((P(G_{1})+P(G_{2}) = 1)\), son las incidencias relativas de los resfriados y la inﬂuenza, y se denominan probabilidades a priori. Se supone que estas probabilidades condicionales y a priori pueden estimarse a partir de las observaciones y de la información acumulada. Entonces la probabilidad \(P(D)\) viene dada por

(4.1)#\[ P(D)=P(G_{1})P(D|G_{1})+P(G_{2})P(D|G_{2}), \]

la probabilidad de que la fiebre sea el resultado de un resfriado o de la inﬂuenza, llamada la ley de la probabilidad total.

En nuestro ejemplo, queremos conocer las probabilidades de que la fiebre que se ha producido, haya sido causada por un resfriado o por la inﬂuenza, respectivamente, representadas por las probabilidades condicionales \(P(G_{1}|D)\) y \(P(G_{2}|D)\). El Teorema de Bayes proporciona estas probabilidades sobre la base de las probabilidades concocidas a priori \(P(G_{i})\) y las probabilidades condicionales \(P(D|G_{i})\). Es decir, las probabilidades condicionales \(P(G_{i}|D)\) vienen dadas por

\[\begin{split} \begin{align*} P(G_{i}|D)&=\frac{P(G_{i}\cap D)}{P(D)}\\ &=\frac{P(G_{i})P(D|G_{i})}{P(G_{1})P(D|G_{1})+P(G_{1})P(D|G_{2})},\quad i=1,2, \end{align*} \end{split}\]

donde \(P(D)\) es la probabilidad total Ecuación (4.1). Tras la aparición del resultado \(D\), las probabilidades condicionales \(P(G_{i}|D)\) se convierten en probabilidades posteriores. En general, el Teorema de Bayes se formula como sigue.

Theorem 4.1 (Teorema de Bayes)

Suponga que el espacio muestral \(\Omega\) es divido en \(r\) eventos mutuamente disyuntos \(G_{j}\) como \(\Omega=G_{1}\cup G_{2}\cup\cdots\cup G_{r}~(G_{i}\cap G_{j}=\emptyset)\). Entonces, para cualquier evento \(D\), la probabilidad condicional \(P(G_{i}|D)\) esta dada por

(4.2)#\[ P(G_{i}|D)=\frac{P(G_{i}\cap D)}{P(D)}=\frac{P(G_{i})P(D|G_{i})}{\displaystyle{\sum_{j=1}^{r}P(G_{j})P(D|G_{j})}},~i=1,2,\dots,r, \]

donde \(~\displaystyle{\sum_{j=1}^{r}P(G_{j})=1}\).

En esta sección, el propósito es realizar clasificación para la asignación de clases de datos \(p\)-dimensionales recién observados, basándose en la probabilidad posterior de su pertenencia a cada clase. Discutimos la aplicación del Teorema de Bayes y la expresión de la probabilidad posterior mediante un modelo de de probabilidad, y el método de formulación de análisis discriminante y cuadrático, para la asignación de clases.

Distribuciones de probabilidad y verosimilitud

Supongamos que tenemos \(n_{1}\) datos \(p\)-dimensionales de la clase \(G_{1}\) y \(n_{2}\) datos \(p\)-dimensionales de la clase \(G_{2}\), y representamos el total \(n=(n_{1}+n_{2})\) datos de entrenamiento como

\[ G_{1}:~\boldsymbol{x}_{1}^{(1)}, \boldsymbol{x}_{2}^{(1)},\dots, \boldsymbol{x}_{n_{1}}^{(1)},\quad G_{2}:~\boldsymbol{x}_{1}^{(2)}, \boldsymbol{x}_{2}^{(2)},\dots, \boldsymbol{x}_{n_{2}}^{(2)} \]

Supongamos que los datos de entrenamiento para las clases \(G_{i}~(i=1,2)\) han sido observados de acuerdo a una distribución normal \(p\)-dimensional \(N_{p}(\boldsymbol{\mu}_{i},\Sigma_{i})\) con vector de medias \(\boldsymbol{\mu}_{i}\) y matrices de varianza-covarianza \(\Sigma_{i}\) como sigue:

(4.3)#\[\begin{split} \begin{align*} G_{1}&: N_{p}(\boldsymbol{\mu}_{1}, \Sigma_{1})\sim\boldsymbol{x}_{1}^{(1)},\boldsymbol{x}_{2}^{(1)},\dots, \boldsymbol{x}_{n_{1}}^{(1)},\\ G_{2}&: N_{p}(\boldsymbol{\mu}_{2}, \Sigma_{2})\sim\boldsymbol{x}_{1}^{(2)},\boldsymbol{x}_{2}^{(2)},\dots, \boldsymbol{x}_{n_{2}}^{(1)}. \end{align*} \end{split}\]

Dado este tipo de modelo de distribución de probabilidad, entonces, si suponemos que cierto dato \(\boldsymbol{x}_{0}\) pertenece a la clase \(G_{1}\) o \(G_{2}\), el nivel relativo de ocurrencia de ese dato en cada clase (la verosimilitud o grado de certeza) puede ser cuantificado por \(f(\boldsymbol{x}_{0}|\boldsymbol{\mu}_{i},\Sigma_{i})\), usando la distribución normal \(p\)-dimensional. Esta corresponde a la probabilidad condicional \(P(D|G_{i})\) descrita por el Teorema de Bayes y puede ser denominada la verosimilitud del dato \(\boldsymbol{x}_{0}\).

Por ejemplo, consideremos una observación, extraida de una distribución normal \(N(170, 6^2)\) asociada con alturas de hombres. Entonces, usando la función de densidad de probabilidad, el nivel relativo de ocurrencia de hombres de 178 cm de altura, puede ser determinado como \(f(178|170, 6^2)\) (ver Fig. 4.1).

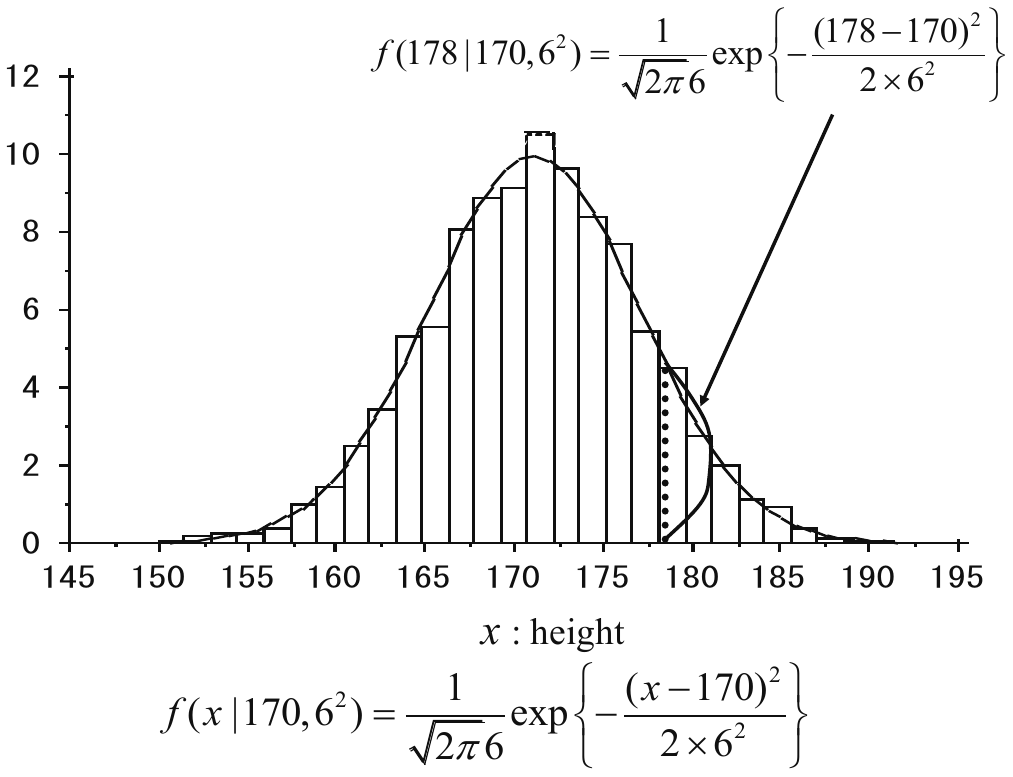
_images/heights_bayes.png — Fig. 4.1 Nivel relativo de ocurrencia \(f(178|170, 6^{2})\). Fuente [Konishi, 2014].#

Para obtener los datos de verosimilitud, reemplazamos los parametros desconocidos, \(\boldsymbol{\mu}_{i}\) y \(\Sigma_{i}\) en Eq. (4.3) con sus respectivas estimaciones de máxima verosimilitud

\[ \overline{\boldsymbol{x}}_{i}=\frac{1}{n_{i}}\sum_{j=1}^{n_{i}}\boldsymbol{x}_{j}^{(i)},\quad S_{i}=\frac{1}{n_{i}}\sum_{j=1}^{n_{i}}(\boldsymbol{x}_{j}^{(i)}-\overline{\boldsymbol{x}}_{i})(\boldsymbol{x}_{j}^{(i)}-\overline{\boldsymbol{x}}_{i})^{T},\quad i=1,2, \]

respectivamente. Aplicando el Teorema de Bayes y utilizando la probabilidad posterior, expresada como una distribución de probabilidad, formulamos la clasificación Bayesiana y derivamos las funciones de discriminación cuadrática y lineal, para la asignación de clases.

Funciones discriminantes

El proposito esencial del análisis discriminante es construir una regla de clasificación basada en datos de entrenamiento, y predecir la pertenencia de datos futuros \(\boldsymbol{x}\) a dos o mas clases predeterminadas.

Pongamos ahora esto en un marco Bayesiano considerando las dos clases \(G_{1}\) y \(G_{2}\). Nuestro objetivo es obtener la probabilidad posterior \(P(G_{i}|D) = P(G_{i}|x)\) cuando el dato \(D = \{x\}\) es observado. Para ello, aplicamos el Teorema de Bayes para obtener la probabilidad posterior, y asignamos los datos futuros \(x\) a la clase con la probabilidad más alta. Así, realizamos una clasificación Bayesiana basada en la razón de las probabilidades posteriores

\[\begin{split} \frac{P(G_{1}|\boldsymbol{x})}{P(G_{2}|\boldsymbol{x})}\quad \begin{cases} \geq 1 & \Rightarrow~\boldsymbol{x}\in G_{1}\\ < 1 & \Rightarrow~\boldsymbol{x}\in G_{2}. \end{cases} \end{split}\]

Tomando logaritmo en ambos lados obtenemos

\[\begin{split} \log\frac{P(G_{1}|\boldsymbol{x})}{P(G_{2}|\boldsymbol{x})}\quad \begin{cases} \geq 0 & \Rightarrow~\boldsymbol{x}\in G_{1}\\ < 0 & \Rightarrow~\boldsymbol{x}\in G_{2}. \end{cases} \end{split}\]

Por el Teorema de Bayes Eq. (4.2), las probabilidades posteriores están dadas por

(4.4)#\[ P(G_{i}|\boldsymbol{x})=\frac{P(G_{i})P(\boldsymbol{x}|G_{i})}{P(G_{1})P(\boldsymbol{x}|G_{1})+P(G_{1})P(\boldsymbol{x}|G_{2})},\quad i=1,2. \]

\(P(G_i \mid \boldsymbol{x})\) es la probabilidad posterior (lo que queremos).
\(P(\boldsymbol{x} \mid G_i)\) es la verosimilitud (probabilidad de ver el dato si perteneciera a \(G_i\)).
\(P(G_i)\) es la probabilidad a priori de esa clase.
\(P(\boldsymbol{x})=P(G_{1})P(\boldsymbol{x}|G_{1})+P(G_{1})P(\boldsymbol{x}|G_{2})\) es la probabilidad total de observar ese dato, sin importar la clase.

Usando las distribuciones normales \(p\)-dimensionales estimadas \(f(\boldsymbol{x}|\overline{\boldsymbol{x}}_{i}, S_{i})~(i=1,2)\), la probabilidad condicional y suponiendo que las clases son igual de probables antes de ver el dato, es decir \(P(G_1) = P(G_2) = 0.5\) se tiene que

\[ P(G_i \mid \boldsymbol{x}) = \frac{P(\boldsymbol{x} \mid G_i)}{P(\boldsymbol{x} \mid G_1) + P(\boldsymbol{x} \mid G_2)} \]

En lugar de escribir \(P(\boldsymbol{x} \mid G_i)\) de forma genérica, dado que cada clase sigue una distribución normal multivariada con media \(\bar{\boldsymbol{x}}_i\) y matriz de covarianza \(S_i\), sustituyendo \(f(\boldsymbol{x} \mid \bar{\boldsymbol{x}}_i, S_i)\) se tiene que

\[ P(G_i \mid \boldsymbol{x}) = \frac{f(\boldsymbol{x} \mid \bar{\boldsymbol{x}}_i, S_i)}{f(\boldsymbol{x} \mid \bar{\boldsymbol{x}}_1, S_1) + f(\boldsymbol{x} \mid \bar{\boldsymbol{x}}_2, S_2)} \]

Cada curva \(f(\boldsymbol{x} \mid \bar{\boldsymbol{x}}_i, S_i)\) representa la densidad de probabilidad de los datos si pertenecieran a cada clase. El valor en el punto \(x\) se usa para comparar qué clase es más probable, y el cociente en la fórmula asegura que la suma de probabilidades posteriores sea

(ver Fig. 4.2) representación del nivel relativo de ocurrencia.

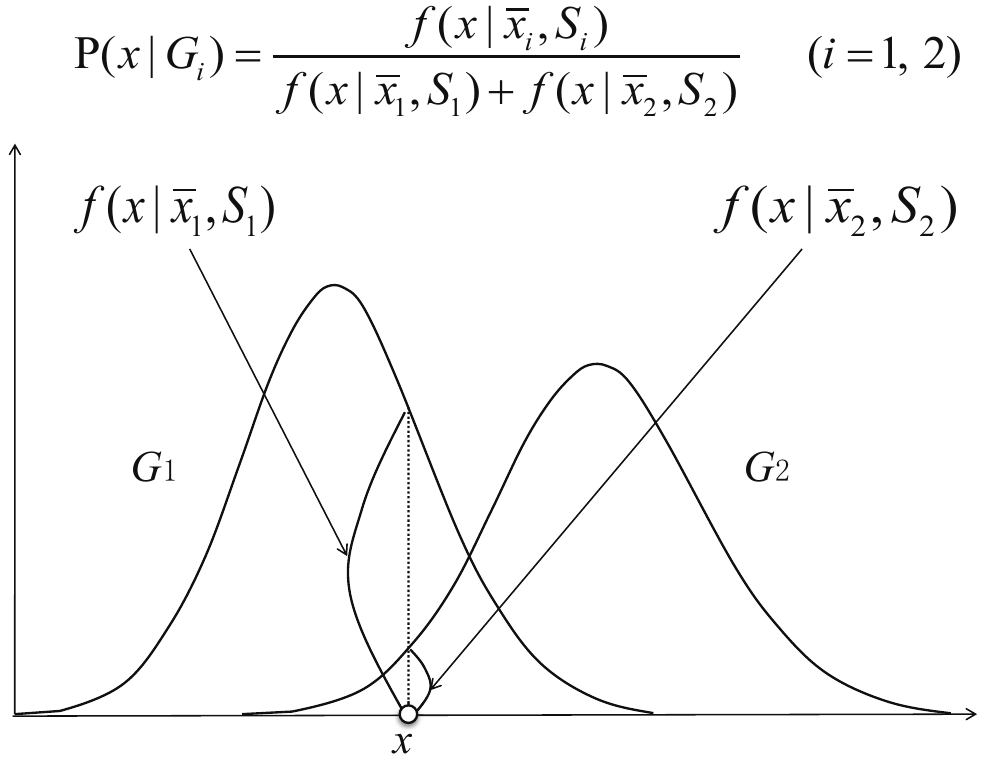
_images/bayes_normal.png — Fig. 4.2 \(P(\boldsymbol{x}|G_{i})\). Nivel relativo de ocurrencia del dato \(\boldsymbol{x}\) en cada clase. Fuente [Konishi, 2014].#

Sustituyendo estas ecuaciones en (4.4), el radio de probabilidades posteriores es expresado como

\[ \frac{P(G_1 \mid \boldsymbol{x})}{P(G_2 \mid \boldsymbol{x})} = \frac{\displaystyle{\frac{P(G_1) P(\boldsymbol{x} \mid G_1)}{P(\boldsymbol{x})}}}{\displaystyle{\frac{P(G_2) P(\boldsymbol{x} \mid G_2)}{P(\boldsymbol{x})}}} = \frac{P(G_1) P(\boldsymbol{x} \mid G_1)}{P(G_2) P(\boldsymbol{x} \mid G_2)} \]

Como se asume que las clases \(G_1\) y \(G_2\) siguen una distribución normal multivariada con media estimada \(\bar{\boldsymbol{x}}_i\) y covarianza estimada \(S_i\), entonces \(P(\boldsymbol{x} \mid G_i) = f(\boldsymbol{x} \mid \bar{\boldsymbol{x}}_i, S_i)\). Por lo tanto

\[ \frac{P(G_1) P(\boldsymbol{x} \mid G_1)}{P(G_2) P(\boldsymbol{x} \mid G_2)} = \frac{P(G_1) f(\boldsymbol{x} \mid \bar{\boldsymbol{x}}_1, S_1)}{P(G_2) f(\boldsymbol{x} \mid \bar{\boldsymbol{x}}_2, S_2)} \]

Tomando el logaritmo de esta expresión, bajo el supuesto de que las probabilidades a priori son iguales, obtenemos la clasificación Bayesiana basada en la distribución de probabilidad

(4.5)#\[\begin{split} h(\boldsymbol{x})=\log\frac{f(\boldsymbol{x}|\overline{\boldsymbol{x}}_{1}, S_{1})}{f(\boldsymbol{x}|\overline{\boldsymbol{x}}_{2}, S_{2})}\quad \begin{cases} \geq 0 &\Rightarrow~\boldsymbol{x}\in G_{1}\\ < 0 &\Rightarrow~\boldsymbol{x}\in G_{2} \end{cases} \end{split}\]

Dada la distribución normal \(p-\)dimensional estimada \(N_{p}(\overline{\boldsymbol{x}}_{i}, S_{i})~(i=1,2)\), se tiene que:

\[ f(\boldsymbol{x}|\boldsymbol{x}_{i}, S_{i})=\frac{1}{(2\pi)^{p/2}|S_{i}|^{1/2}}\exp\left[-\frac{1}{2}(\boldsymbol{x}-\overline{\boldsymbol{x}}_{i})^{T}S_{i}^{-1}(\boldsymbol{x}-\overline{\boldsymbol{x}}_{i})\right] \]

Entonces, la función discriminante \(h(\boldsymbol{x})\) esta dada por:

(4.6)#\[\begin{split} \begin{align*} h(\boldsymbol{x})&=\log f(\boldsymbol{x}|\overline{\boldsymbol{x}}_{1}, S_{1})-\log f(\boldsymbol{x}|\overline{\boldsymbol{x}}_{2}, S_{2})\\[2mm] &=\log\left\{\left[(2\pi)^{p}|S_{1}|\right]^{-1/2}\right\}+\log\left\{\exp\left[-\frac{1}{2}(\boldsymbol{x}-\overline{\boldsymbol{x}}_{1})^{T}S_{1}^{-1}(\boldsymbol{x}-\overline{\boldsymbol{x}}_{1})\right]\right\}\\ &-\log\left\{\left[(2\pi)^{p}|S_{2}|\right]^{-1/2}\right\}-\log\left\{\exp\left[-\frac{1}{2}(\boldsymbol{x}-\overline{\boldsymbol{x}}_{2})^{T}S_{2}^{-1}(\boldsymbol{x}-\overline{\boldsymbol{x}}_{2})\right]\right\}\\ &=\frac{1}{2}\left\{(\boldsymbol{x}-\overline{\boldsymbol{x}}_{2})^{T}S_{2}^{-1}(\boldsymbol{x}-\overline{\boldsymbol{x}}_{2})-(\boldsymbol{x}-\overline{\boldsymbol{x}}_{1})^{T}S_{1}^{-1}(\boldsymbol{x}-\overline{\boldsymbol{x}}_{1})-\log\left(\frac{|S_{1}|}{|S_{2}|}\right)\right\}. \end{align*} \end{split}\]

La función \(h(\boldsymbol{x})\) de la Eq. (4.6) es conocida como función discriminante cuadratica. Reemplazando \(S_{i}\) con la matriz de varianza-covarianza de la muestra conjunta \(S=(n_{1}S_{1}+n_{2}S_{2})/(n_{1}+n_{2})\), la función discriminante es además reducida a la función discriminante lineal (verifíquelo)

\[ h(\boldsymbol{x}) = \frac{1}{2}(\boldsymbol{x} - \boldsymbol{x}_2)^T S^{-1} (\boldsymbol{x} - \boldsymbol{x}_2) - \frac{1}{2}(\boldsymbol{x} - \boldsymbol{x}_1)^T S^{-1} (\boldsymbol{x} - \boldsymbol{x}_1) \]

Expandamos cada término:

\[ (\boldsymbol{x} - \boldsymbol{x}_2)^T S^{-1} (\boldsymbol{x} - \boldsymbol{x}_2) = \boldsymbol{x}^T S^{-1} \boldsymbol{x} - 2 \boldsymbol{x}_2^T S^{-1} \boldsymbol{x} + \boldsymbol{x}_2^T S^{-1} \boldsymbol{x}_2 \]

\[ (\boldsymbol{x} - \boldsymbol{x}_1)^T S^{-1} (\boldsymbol{x} - \boldsymbol{x}_1) = \boldsymbol{x}^T S^{-1} \boldsymbol{x} - 2 \boldsymbol{x}_1^T S^{-1} \boldsymbol{x} + \boldsymbol{x}_1^T S^{-1} \boldsymbol{x}_1 \]

Sustituyendo en la función discriminante dentro de la resta:

\[\begin{split} \begin{aligned} h(\boldsymbol{x}) &= \frac{1}{2} \left( \boldsymbol{x}^T S^{-1} \boldsymbol{x} - 2 \boldsymbol{x}_2^T S^{-1} \boldsymbol{x} + \boldsymbol{x}_2^T S^{-1} \boldsymbol{x}_2 \right) \\ &\quad - \frac{1}{2} \left( \boldsymbol{x}^T S^{-1} \boldsymbol{x} - 2 \boldsymbol{x}_1^T S^{-1} \boldsymbol{x} + \boldsymbol{x}_1^T S^{-1} \boldsymbol{x}_1 \right) \end{aligned} \end{split}\]

Los términos \(\boldsymbol{x}^T S^{-1} \boldsymbol{x}\) se cancelan entre sí, ya que aparecen con el mismo signo y factor. Entonces queda:

\[\begin{split} \begin{aligned} h(\boldsymbol{x}) &= \frac{1}{2} \left( -2 \boldsymbol{x}_2^T S^{-1} \boldsymbol{x} + \boldsymbol{x}_2^T S^{-1} \boldsymbol{x}_2 + 2 \boldsymbol{x}_1^T S^{-1} \boldsymbol{x} - \boldsymbol{x}_1^T S^{-1} \boldsymbol{x}_1 \right) \\ &= \left( \boldsymbol{x}_1^T S^{-1} - \boldsymbol{x}_2^T S^{-1} \right) \boldsymbol{x} + \frac{1}{2} \left( \boldsymbol{x}_2^T S^{-1} \boldsymbol{x}_2 - \boldsymbol{x}_1^T S^{-1} \boldsymbol{x}_1 \right) \end{aligned} \end{split}\]

La expresión anterior se puede reescribir como:

\[ h(\boldsymbol{x}) = \mathbf{w}^T \boldsymbol{x} + w_0 \]

donde:

\(\mathbf{w} = S^{-1} (\boldsymbol{x}_1 - \boldsymbol{x}_2)\)
\(w_0 = \frac{1}{2} \left( \boldsymbol{x}_2^T S^{-1} \boldsymbol{x}_2 - \boldsymbol{x}_1^T S^{-1} \boldsymbol{x}_1 \right)\)

Por lo tanto,

\[ h(\boldsymbol{x}) = (\boldsymbol{x}_1 - \boldsymbol{x}_2)^T S^{-1} \boldsymbol{x} - \frac{1}{2} \left( \boldsymbol{x}_1^T S^{-1} \boldsymbol{x}_1 - \boldsymbol{x}_2^T S^{-1} \boldsymbol{x}_2 \right). \]

De esta forma, obtenemos la regla de clasificación de Bayes (4.5) basada en el signo del logaritmo de la razón entre la distribución de probabilidad estimada que caracteriza la clase. La función \(h(\boldsymbol{x})\) expresada por la distribución normal \(p\)-dimensional entrega las funciones discriminantes, lineales y cuadráticas.

4.2. Aplicación: Titanic Dataset#

El Titanic, barco británico de la White Star Line, se hundió en el Atlántico Norte el 15 de abril de 1912 después de golpear un iceberg en su viaje de Southampton a Nueva York. A bordo había 2,224 personas, incluyendo pasajeros y tripulación, y 1,514 murieron.
El Titanic tenía 16 botes salvavidas de madera y cuatro plegables, suficientes para solo 1,178 personas, un tercio de su capacidad total y el 53% de los pasajeros reales. En ese momento, los botes salvavidas se usaban para trasladar a los sobrevivientes a otros barcos, no para mantener a flote o llevar a todos a la costa.
La pregunta principal es ¿quiénes tenían más probabilidades de sobrevivir en esta tragedia?.

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB, BernoulliNB
from sklearn.metrics import accuracy_score
import numpy as np

import warnings
warnings.filterwarnings('ignore')
import mglearn
import matplotlib

train_data = pd.read_csv('https://raw.githubusercontent.com/lihkir/Data/main/train_titanic.csv')
test_data  = pd.read_csv('https://raw.githubusercontent.com/lihkir/Data/main/test_titanic.csv')

frames = [train_data, test_data]
all_data = pd.concat(frames, sort = False)

print('All data shape: ', all_data.shape)
all_data.head()

All data shape:  (1309, 12)

	PassengerId	Survived	Pclass	Name	Sex	Age	SibSp	Ticket	Fare	Cabin	Embarked
0	1	0.0	3	Braund, Mr. Owen Harris	male	22.0	1	A/5 21171	7.2500	NaN	S
1	2	1.0	1	Cumings, Mrs. John Bradley (Florence Briggs Th...	female	38.0	1	PC 17599	71.2833	C85	C
2	3	1.0	3	Heikkinen, Miss. Laina	female	26.0	0	STON/O2. 3101282	7.9250	NaN	S
3	4	1.0	1	Futrelle, Mrs. Jacques Heath (Lily May Peel)	female	35.0	1	113803	53.1000	C123	S
4	5	0.0	3	Allen, Mr. William Henry	male	35.0	0	373450	8.0500	NaN	S

Análisis Exploratorio de Datos (EDA)

train_data.head()

	PassengerId	Survived	Pclass	Name	Sex	Age	SibSp	Ticket	Fare	Cabin	Embarked
0	1	0	3	Braund, Mr. Owen Harris	male	22.0	1	A/5 21171	7.2500	NaN	S
1	2	1	1	Cumings, Mrs. John Bradley (Florence Briggs Th...	female	38.0	1	PC 17599	71.2833	C85	C
2	3	1	3	Heikkinen, Miss. Laina	female	26.0	0	STON/O2. 3101282	7.9250	NaN	S
3	4	1	1	Futrelle, Mrs. Jacques Heath (Lily May Peel)	female	35.0	1	113803	53.1000	C123	S
4	5	0	3	Allen, Mr. William Henry	male	35.0	0	373450	8.0500	NaN	S

train_data.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 891 entries, 0 to 890
Data columns (total 12 columns):
 #   Column       Non-Null Count  Dtype  
---  ------       --------------  -----  
 0   PassengerId  891 non-null    int64  
 1   Survived     891 non-null    int64  
 2   Pclass       891 non-null    int64  
 3   Name         891 non-null    object 
 4   Sex          891 non-null    object 
 5   Age          714 non-null    float64
 6   SibSp        891 non-null    int64  
 7   Parch        891 non-null    int64  
 8   Ticket       891 non-null    object 
 9   Fare         891 non-null    float64
 10  Cabin        204 non-null    object 
 11  Embarked     889 non-null    object 
dtypes: float64(2), int64(5), object(5)
memory usage: 83.7+ KB

train_data.describe()

	PassengerId	Survived	Pclass	Age	SibSp	Parch	Fare
count	891.000000	891.000000	891.000000	714.000000	891.000000	891.000000	891.000000
mean	446.000000	0.383838	2.308642	29.699118	0.523008	0.381594	32.204208
std	257.353842	0.486592	0.836071	14.526497	1.102743	0.806057	49.693429
min	1.000000	0.000000	1.000000	0.420000	0.000000	0.000000	0.000000
25%	223.500000	0.000000	2.000000	20.125000	0.000000	0.000000	7.910400
50%	446.000000	0.000000	3.000000	28.000000	0.000000	0.000000	14.454200
75%	668.500000	1.000000	3.000000	38.000000	1.000000	0.000000	31.000000
max	891.000000	1.000000	3.000000	80.000000	8.000000	6.000000	512.329200

test_data.head()

	PassengerId	Pclass	Name	Sex	Age	SibSp	Parch	Ticket	Fare	Cabin	Embarked
0	892	3	Kelly, Mr. James	male	34.5	0	0	330911	7.8292	NaN	Q
1	893	3	Wilkes, Mrs. James (Ellen Needs)	female	47.0	1	0	363272	7.0000	NaN	S
2	894	2	Myles, Mr. Thomas Francis	male	62.0	0	0	240276	9.6875	NaN	Q
3	895	3	Wirz, Mr. Albert	male	27.0	0	0	315154	8.6625	NaN	S
4	896	3	Hirvonen, Mrs. Alexander (Helga E Lindqvist)	female	22.0	1	1	3101298	12.2875	NaN	S

test_data.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 418 entries, 0 to 417
Data columns (total 11 columns):
 #   Column       Non-Null Count  Dtype  
---  ------       --------------  -----  
 0   PassengerId  418 non-null    int64  
 1   Pclass       418 non-null    int64  
 2   Name         418 non-null    object 
 3   Sex          418 non-null    object 
 4   Age          332 non-null    float64
 5   SibSp        418 non-null    int64  
 6   Parch        418 non-null    int64  
 7   Ticket       418 non-null    object 
 8   Fare         417 non-null    float64
 9   Cabin        91 non-null     object 
 10  Embarked     418 non-null    object 
dtypes: float64(2), int64(4), object(5)
memory usage: 36.0+ KB

test_data.describe()

	PassengerId	Pclass	Age	SibSp	Parch	Fare
count	418.000000	418.000000	332.000000	418.000000	418.000000	417.000000
mean	1100.500000	2.265550	30.272590	0.447368	0.392344	35.627188
std	120.810458	0.841838	14.181209	0.896760	0.981429	55.907576
min	892.000000	1.000000	0.170000	0.000000	0.000000	0.000000
25%	996.250000	1.000000	21.000000	0.000000	0.000000	7.895800
50%	1100.500000	3.000000	27.000000	0.000000	0.000000	14.454200
75%	1204.750000	3.000000	39.000000	1.000000	0.000000	31.500000
max	1309.000000	3.000000	76.000000	8.000000	9.000000	512.329200

Identifiquemos si existen datos faltantes en el dataset. Antes, veamos una breve descripción de cada variable
- PassengerId: identificador único
- Survived: 0=No, 1=Yes
- Pclass: Clase de tiquete. 1 = 1st: Upper, 2 = 2nd: Middle, 3 = 3rd: Lower
- Name: nombre completo con un título
- Sex: genero
- Age: la edad es una fracción si es inferior a 1. Si la edad es estimada, es en forma de xx.5
- Sibsp: número de hermanos / cónyuges a bordo del Titanic. El conjunto de datos define las relaciones familiares de esta manera:
  - Sibling = hermano, hermana, hermanastro, hermanastra
  - Spouse = marido, mujer (se ignoraba a las amantes y prometidas)
- Parch: Número de padres / hijos a bordo del Titanic. El conjunto de datos define las relaciones familiares de esta manera:
  - Parent = madre, padre
  - Child = hija, hijo, hijastra, hijastro
  - Algunos niños viajaban sólo con niñera, por lo que parch=0 para ellos.
- Ticket: número del tiquete
- Fare: tarifa del pasajero
- Cabin: numero de cabina
- Embarked: puerto de embarque

Comprobamos si hay datos faltantes, NA en el conjunto de datos

all_data_NA = all_data.isna().sum()
train_NA = train_data.isna().sum()
test_NA = test_data.isna().sum()

pd.concat([train_NA, test_NA, all_data_NA], axis=1, sort = False, keys = ['Train NA', 'Test NA', 'All NA'])

	Train NA	Test NA	All NA
PassengerId	0	0.0	0
Survived	0	NaN	418
Pclass	0	0.0	0
Name	0	0.0	0
Sex	0	0.0	0
Age	177	86.0	263
SibSp	0	0.0	0
Parch	0	0.0	0
Ticket	0	0.0	0
Fare	0	1.0	1
Cabin	687	327.0	1014
Embarked	2	0.0	2

En total faltan 263 valores de Edad, 1 de Tarifa, 1014 NA en la variable Cabina y 2 en la variable Embarcado. 418 NA en la variable Survived debido a la ausencia de esta información en el conjunto de datos de prueba.
En este ejemplo, no imputaremos estas pérdidas. Técnicas de imputación de datos serán estudiadas en el curso Visualización de Datos para la Toma de Decisiones.

Calculemos y visualicemos la distribución de nuestra variable objetivo: 'Survived'.

labels = (all_data['Survived'].value_counts())
labels

Survived
0.0    549
1.0    342
Name: count, dtype: int64

ax = sns.countplot(x = 'Survived', data = all_data, palette=["#3f3e6fd1", "#85c6a9"])
plt.xticks(np.arange(2), ['drowned', 'survived'])
plt.title('Overall survival (training dataset)',fontsize= 14)
plt.xlabel('Passenger status after the tragedy')
plt.ylabel('Number of passengers');

for i, v in enumerate(labels):
    ax.text(i, v-40, str(v), horizontalalignment = 'center', size = 14, color = 'w', fontweight = 'bold');

_images/643b21f6def103581edac289b33459b9df67b84b915c74ec37fd087857aedb7b.png

all_data['Survived'].value_counts(normalize = True)

Survived
0.0    0.616162
1.0    0.383838
Name: proportion, dtype: float64

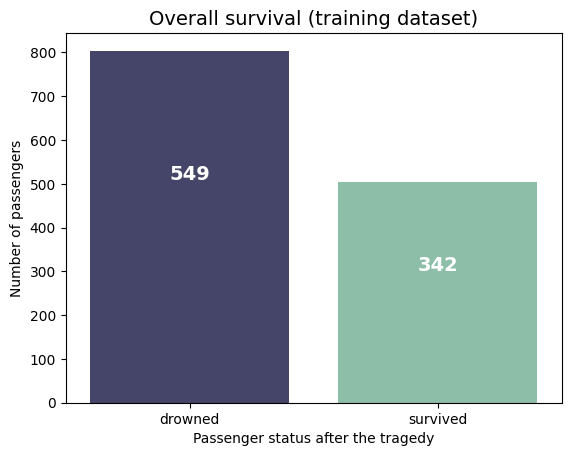
Tenemos 891 pasajeros en el conjunto de datos, 549 (61,6%) de ellos se ahogaron y sólo 342 (38,4%) sobrevivieron. Pero sabemos que los botes salvavidas podían transportar al 53% del total de pasajeros. Veamos la distribución de las edades. Usamos para estimar la distribución de probabilidad el método no paramétrico KDE (ver Kernel density estimation ).

sns.distplot(all_data[(all_data["Age"] > 0)].Age, kde_kws={"lw": 3}, bins = 50)
plt.title('Distrubution of passengers age (all data)',fontsize= 14)
plt.xlabel('Age')
plt.ylabel('Frequency')
plt.tight_layout()

_images/378da6a8ed013c518acf4623f3a1ff678234755d2a0da64775f6a3457908f448.png

age_distr = pd.DataFrame(all_data['Age'].describe())
age_distr.transpose()

	count	mean	std	min	25%	50%	75%	max
Age	1046.0	29.881138	14.413493	0.17	21.0	28.0	39.0	80.0

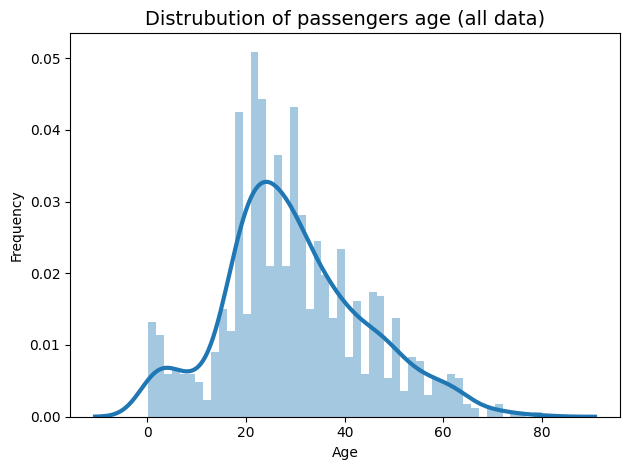
La distribución de la edad está ligeramente sesgada a la derecha. La edad varía entre 0.17 y 80 años, con una media = 29.88. ¿Influyó mucho la edad en las posibilidades de sobrevivir? Visualizamos dos distribuciones de edad, agrupadas por estatus de supervivencia.

plt.figure(figsize=(8, 4))
sns.boxplot(y = 'Survived', x = 'Age', data = train_data, palette=["#3f3e6fd1", "#85c6a9"], fliersize = 0, orient = 'h')
sns.stripplot(y = 'Survived', x = 'Age', data = train_data, linewidth = 0.6, palette=["#3f3e6fd1", "#85c6a9"], orient = 'h')
plt.yticks( np.arange(2), ['drowned', 'survived'])
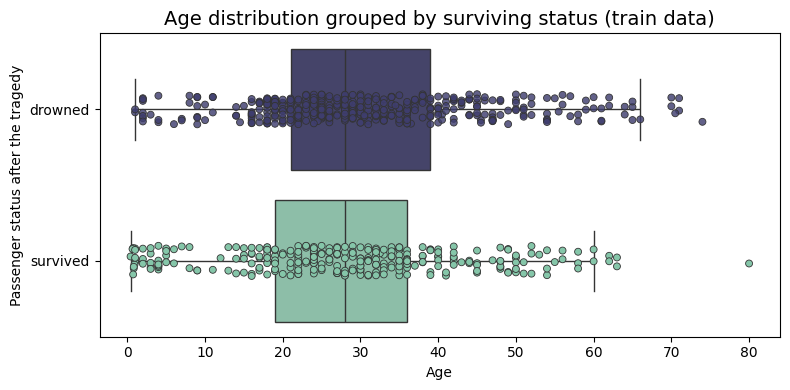
plt.title('Age distribution grouped by surviving status (train data)',fontsize= 14)
plt.ylabel('Passenger status after the tragedy')
plt.tight_layout()

_images/ae9b1b98189ed96c689b505a3aded26b8d07ee183cc35cacead8392bb9337998.png

pd.DataFrame(all_data.groupby('Survived')['Age'].describe())

	count	mean	std	min	25%	50%	75%	max
Survived
0.0	424.0	30.626179	14.172110	1.00	21.0	28.0	39.0	74.0
1.0	290.0	28.343690	14.950952	0.42	19.0	28.0	36.0	80.0

La media de edad de los pasajeros supervivientes es de 28,34 años, 2,28 menos que la media de edad de los pasajeros ahogados (los únicos de los que conocemos su estado de supervivencia). La edad mínima de los pasajeros ahogados es de 1 año, lo que es muy triste. La edad máxima de los pasajeros ahogados es de 80 años. Verifiquemos si existe un error.

all_data[all_data['Age'] == max(all_data['Age'] )]

	PassengerId	Survived	Pclass	Name	Sex	Age	SibSp	Parch	Ticket	Fare	Cabin	Embarked
630	631	1.0	1	Barkworth, Mr. Algernon Henry Wilson	male	80.0	0	0	27042	30.0	A23	S

Sr. Algernon Henry Barkworth nació el 4 de junio de 1864, tenía 48 años en 1912 y murió en 1945 a los 80 años (ver Algernon Henry Wilson Barkworth (1864 - 1945)).

train_data.loc[train_data['PassengerId'] == 631, 'Age'] = 48
all_data.loc[all_data['PassengerId'] == 631, 'Age'] = 48

pd.DataFrame(all_data.groupby('Survived')['Age'].describe())

	count	mean	std	min	25%	50%	75%	max
Survived
0.0	424.0	30.626179	14.172110	1.00	21.0	28.0	39.0	74.0
1.0	290.0	28.233345	14.684091	0.42	19.0	28.0	36.0	63.0

La media de edad de los pasajeros supervivientes es de 28,23 años, 2,39 menos que la media de edad de los pasajeros ahogados(los únicos de los que conocemos el estado de supervivencia). Parece que hay más posibilidades de sobrevivir para los jóvenes.

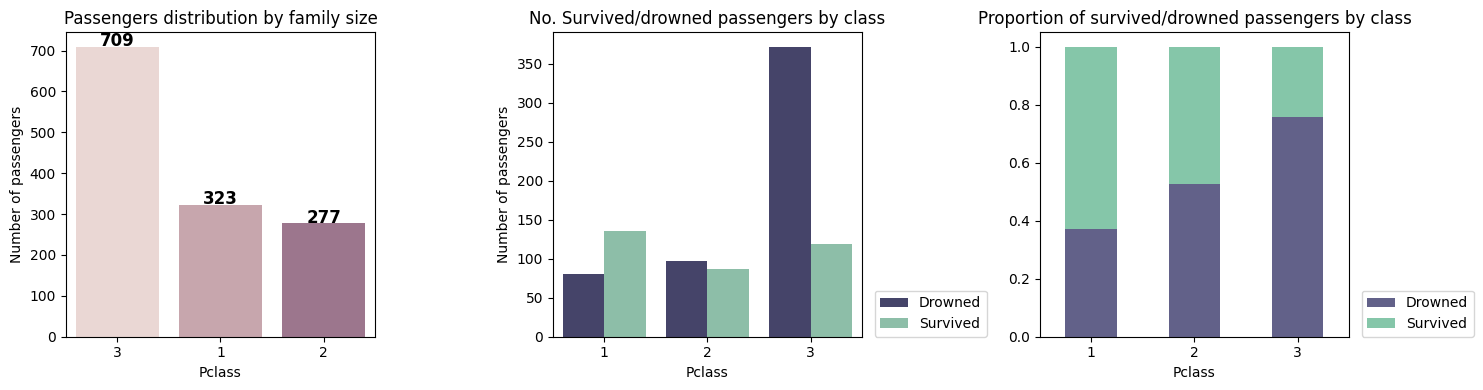
Podemos ahora, verificar cuantos pasajeros existen por cada clase (Pclass), y además, identificar frecuencia y proporción de ahogados, por cada una de las tres clases

fig = plt.figure(figsize = (15,4))

ax1 = fig.add_subplot(131)
ax = sns.countplot(x=all_data['Pclass'], palette = ['#eed4d0', '#cda0aa', '#a2708e'], 
                   order = all_data['Pclass'].value_counts(sort = False).index)
labels = (all_data['Pclass'].value_counts(sort = False))

for i, v in enumerate(labels):
    ax.text(i, v+2, str(v), horizontalalignment = 'center', size = 12, color = 'black', fontweight = 'bold')
    
plt.title('Passengers distribution by family size')
plt.ylabel('Number of passengers')
plt.tight_layout()

ax2 = fig.add_subplot(132)
sns.countplot(x = 'Pclass', hue = 'Survived', data = all_data, palette=["#3f3e6fd1", "#85c6a9"], ax = ax2)
plt.title('No. Survived/drowned passengers by class')
plt.ylabel('Number of passengers')
plt.legend(( 'Drowned', 'Survived'), loc=(1.04,0))
_ = plt.xticks(rotation=False)

ax3 = fig.add_subplot(133)
d = all_data.groupby('Pclass')['Survived'].value_counts(normalize = True).unstack()
d.plot(kind='bar', stacked='True', ax = ax3, color =["#3f3e6fd1", "#85c6a9"])
plt.title('Proportion of survived/drowned passengers by class')
plt.legend(( 'Drowned', 'Survived'), loc=(1.04,0))
_ = plt.xticks(rotation=False)

plt.tight_layout()

_images/f842568175750205ca0b232ea001dc59f064c51a152d27543b8b88c5321c05fb.png

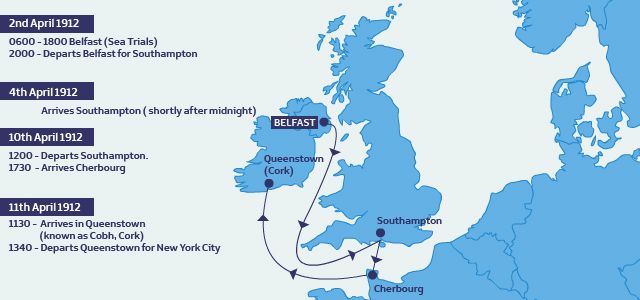
El Titanic tenía 3 puntos de embarque antes de que el buque iniciara su ruta hacia Nueva York
- Southampton
- Cherbourg
- Queenstown

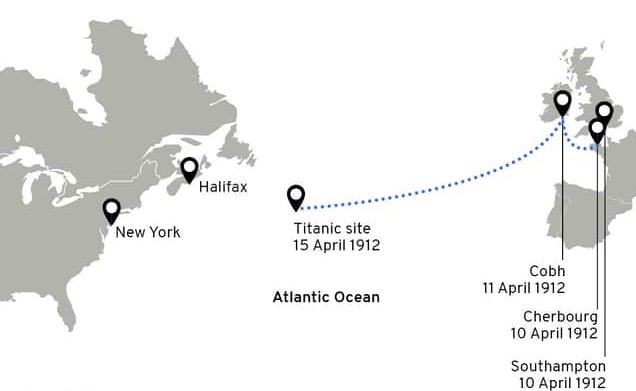
Este análisis explotario se puede extender aún mas, y estudiar por ejemplo, ditribución de pasajeros por títulos, ubicación de las cabinas en el barco, tamaño de las familias, cantidad de pasajeros por clase, genero entre otros. Queda como ejercicio para el estudiante, extender el análisis de cada uno de estos casos.

Creamos dos nuevos dataframe, df_train_ml y df_test_ml sólo tendrán características ordinales y no tendrán datos faltantes. Para que puedan ser utilizados por los algoritmos de ML, realizamos conversión de categórico a numérico mediante pd.get_dummies eliminando todas las características que no parezcan útiles para la predicción. A continuación, utilizamos el escalador estándar y aplicamos la división train/test

df_train_ml = train_data.copy()
df_test_ml  = test_data.copy()

df_train_ml.head()

	PassengerId	Survived	Pclass	Name	Sex	Age	SibSp	Ticket	Fare	Cabin	Embarked
0	1	0	3	Braund, Mr. Owen Harris	male	22.0	1	A/5 21171	7.2500	NaN	S
1	2	1	1	Cumings, Mrs. John Bradley (Florence Briggs Th...	female	38.0	1	PC 17599	71.2833	C85	C
2	3	1	3	Heikkinen, Miss. Laina	female	26.0	0	STON/O2. 3101282	7.9250	NaN	S
3	4	1	1	Futrelle, Mrs. Jacques Heath (Lily May Peel)	female	35.0	1	113803	53.1000	C123	S
4	5	0	3	Allen, Mr. William Henry	male	35.0	0	373450	8.0500	NaN	S

df_train_ml.drop(['PassengerId', 'Name', 'Ticket', 'Cabin'], axis=1, inplace=True)
df_train_ml.dropna(inplace=True)

df_train_ml.head(10)

	Survived	Pclass	Sex	Age	SibSp	Parch	Fare	Embarked
0	0	3	male	22.0	1	0	7.2500	S
1	1	1	female	38.0	1	0	71.2833	C
2	1	3	female	26.0	0	0	7.9250	S
3	1	1	female	35.0	1	0	53.1000	S
4	0	3	male	35.0	0	0	8.0500	S
6	0	1	male	54.0	0	0	51.8625	S
7	0	3	male	2.0	3	1	21.0750	S
8	1	3	female	27.0	0	2	11.1333	S
9	1	2	female	14.0	1	0	30.0708	C
10	1	3	female	4.0	1	1	16.7000	S

df_test_ml.drop(['PassengerId', 'Name', 'Ticket', 'Cabin'], axis=1, inplace=True)
df_test_ml.dropna(inplace=True)

df_test_ml.head(10)

	Pclass	Sex	Age	SibSp	Parch	Fare	Embarked
0	3	male	34.5	0	0	7.8292	Q
1	3	female	47.0	1	0	7.0000	S
2	2	male	62.0	0	0	9.6875	Q
3	3	male	27.0	0	0	8.6625	S
4	3	female	22.0	1	1	12.2875	S
5	3	male	14.0	0	0	9.2250	S
6	3	female	30.0	0	0	7.6292	Q
7	2	male	26.0	1	1	29.0000	S
8	3	female	18.0	0	0	7.2292	C
9	3	male	21.0	2	0	24.1500	S

Con el objetivo de evitar (dummy variable trap), eliminamos la primera columna (puede ser cualquier otra).

Dummy variable trap

La trampa de la variable dummy es un escenario en el que hay atributos que están muy correlacionados (multicolineales) y una variable predice el valor de otras. Cuando utilizamos la codificación de una sola variable para tratar los datos categóricos, una variable dummy (atributo) puede predecirse con la ayuda de otras variables dummy.
La utilización de todas las variables dummies en modelos de ML conduce a una trampa de variables dummy. Por lo tanto, los modelos de ML deben diseñarse para excluir una variable dummy.

cat_columns = ['Sex', 'Embarked', 'Pclass'];

df_train_ml = pd.get_dummies(df_train_ml, columns=cat_columns, drop_first=True)
df_train_ml.replace({False: 0, True: 1}, inplace=True)

df_train_ml.head(10)

	Survived	Age	SibSp	Parch	Fare	Sex_male	Embarked_S	Pclass_2	Pclass_3
0	0	22.0	1	0	7.2500	1	1	0	1
1	1	38.0	1	0	71.2833	0	0	0	0
2	1	26.0	0	0	7.9250	0	1	0	1
3	1	35.0	1	0	53.1000	0	1	0	0
4	0	35.0	0	0	8.0500	1	1	0	1
6	0	54.0	0	0	51.8625	1	1	0	0
7	0	2.0	3	1	21.0750	1	1	0	1
8	1	27.0	0	2	11.1333	0	1	0	1
9	1	14.0	1	0	30.0708	0	0	1	0
10	1	4.0	1	1	16.7000	0	1	0	1

df_test_ml = pd.get_dummies(df_test_ml, columns=cat_columns, drop_first=True)
df_test_ml.replace({False: 0, True: 1}, inplace=True)

df_test_ml.head(10)

	Age	SibSp	Parch	Fare	Sex_male	Embarked_Q	Embarked_S	Pclass_2	Pclass_3
0	34.5	0	0	7.8292	1	1	0	0	1
1	47.0	1	0	7.0000	0	0	1	0	1
2	62.0	0	0	9.6875	1	1	0	1	0
3	27.0	0	0	8.6625	1	0	1	0	1
4	22.0	1	1	12.2875	0	0	1	0	1
5	14.0	0	0	9.2250	1	0	1	0	1
6	30.0	0	0	7.6292	0	1	0	0	1
7	26.0	1	1	29.0000	1	0	1	1	0
8	18.0	0	0	7.2292	0	0	0	0	1
9	21.0	2	0	24.1500	1	0	1	0	1

df_train_ml.info()

<class 'pandas.core.frame.DataFrame'>
Index: 712 entries, 0 to 890
Data columns (total 10 columns):
 #   Column      Non-Null Count  Dtype  
---  ------      --------------  -----  
 0   Survived    712 non-null    int64  
 1   Age         712 non-null    float64
 2   SibSp       712 non-null    int64  
 3   Parch       712 non-null    int64  
 4   Fare        712 non-null    float64
 5   Sex_male    712 non-null    int64  
 6   Embarked_Q  712 non-null    int64  
 7   Embarked_S  712 non-null    int64  
 8   Pclass_2    712 non-null    int64  
 9   Pclass_3    712 non-null    int64  
dtypes: float64(2), int64(8)
memory usage: 61.2 KB

df_test_ml.info()

<class 'pandas.core.frame.DataFrame'>
Index: 331 entries, 0 to 415
Data columns (total 9 columns):
 #   Column      Non-Null Count  Dtype  
---  ------      --------------  -----  
 0   Age         331 non-null    float64
 1   SibSp       331 non-null    int64  
 2   Parch       331 non-null    int64  
 3   Fare        331 non-null    float64
 4   Sex_male    331 non-null    int64  
 5   Embarked_Q  331 non-null    int64  
 6   Embarked_S  331 non-null    int64  
 7   Pclass_2    331 non-null    int64  
 8   Pclass_3    331 non-null    int64  
dtypes: float64(2), int64(7)
memory usage: 25.9 KB

Calculemos ahora matriz de correlación, para el conjunto de entrenamiento df_train_ml

corr = df_train_ml.corr()

f,ax = plt.subplots(figsize=(9,6))
sns.heatmap(corr, annot = True, linewidths=1.5 , fmt = '.2f',ax=ax)
plt.show()

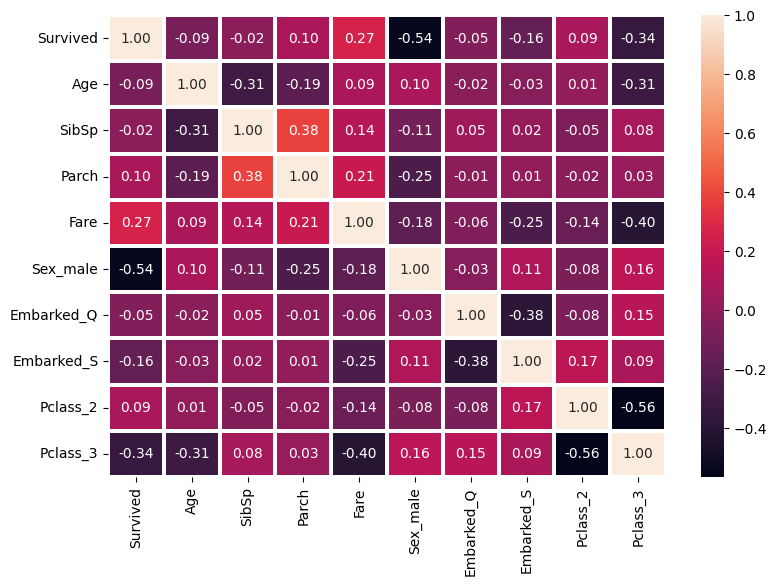
_images/b491d1043db1e724ad51c5deb4525a2e3d4b944cfe108108aa5f6f9f21102447.png

Dividimos nuestro dataset df_train_ml en, conjunto de entrenamiento y de prueba. Posteriormente, escalamos la partición de entrenamiento usando StandardScaler.

from sklearn.pipeline import Pipeline
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.preprocessing import StandardScaler
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import accuracy_score

X = df_train_ml.drop('Survived', axis=1)
y = df_train_ml['Survived']

GaussianNB Es el modelo recomendado para este problema, por las siguientes razones:
- Úsalo cuando tienes variables numéricas continuas, como Age, Fare.
- Funciona bien con mezclas de variables numéricas y discretas.
- Las variables categóricas deben ser convertidas (por ejemplo, con OneHotEncoding o LabelEncoding).
- Es el más adecuado para el dataset Titanic después de preprocesar.

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30, random_state=101)

pipe = Pipeline([
    ('scaler', StandardScaler()),
    ('clf', GaussianNB())
])

param_grid = {}

grid = GridSearchCV(pipe, param_grid, cv=5, scoring='roc_auc')
grid.fit(X_train, y_train)

y_pred = grid.predict(X_test)
acc = accuracy_score(y_test, y_pred)
print(f'Accuracy: {acc:.4f}')

Accuracy: 0.7757

No necesitas escalar manualmente el test, porque el scaler que está dentro del Pipeline se aplica automáticamente cuando llamas a:

grid.predict(X_test)

El flujo es así:

X_test entra al pipeline.
El paso scaler (StandardScaler) transforma los datos usando la media y desviación aprendidas en X_train.
El resultado escalado pasa al clasificador GaussianNB.

Si aun así quisieras usar explícitamente el scaler entrenado (por ejemplo, para inspeccionar o transformar datos fuera del pipeline), el que debes usar es:

modelo_entrenado = grid.best_estimator_.named_steps['clf']
scaler_entrenado = grid.best_estimator_.named_steps['scaler']

X_test_scaled = scaler_entrenado.transform(X_test)
y_pred_scaled = modelo_entrenado.predict(X_test_scaled)

acc = accuracy_score(y_test, y_pred_scaled)
print(f'Accuracy: {acc:.4f}')

Accuracy: 0.7757

Ese scaler_entrenado es exactamente el mismo que el pipeline usa internamente para escalar tu test. Lo importante: nunca se reentrena con el test, solo aplica las estadísticas aprendidas del train.

import pandas as pd
import numpy as np
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import train_test_split
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import OneHotEncoder, StandardScaler
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import classification_report, accuracy_score

import pandas as pd
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import OneHotEncoder, StandardScaler
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import accuracy_score, classification_report

df = pd.read_csv('https://raw.githubusercontent.com/lihkir/Data/main/train_titanic.csv')

df.drop(['PassengerId', 'Name', 'Ticket', 'Cabin'], axis=1, inplace=True)
df.dropna(inplace=True)

X = df.drop("Survived", axis=1)
y = df["Survived"]

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.30, random_state=101
)

categorical_cols = ["Sex", "Embarked", "Pclass"]
numerical_cols = ["Age", "SibSp", "Parch", "Fare"]

preprocessor = ColumnTransformer(transformers=[
    ("cat", OneHotEncoder(drop="first", handle_unknown='ignore'), categorical_cols),
    ("num", StandardScaler(), numerical_cols)
])

pipeline = Pipeline(steps=[
    ("preprocessing", preprocessor),
    ("classifier", GaussianNB())
])

grid_search = GridSearchCV(pipeline, {}, cv=5, scoring='roc_auc')
grid_search.fit(X_train, y_train)

y_pred_hot = grid_search.predict(X_test)
acc = accuracy_score(y_test, y_pred_hot)

print(f"Mejor precisión en validación cruzada: {grid_search.best_score_:.4f}")
print(f"Accuracy en test: {acc:.4f}")
print("\nReporte de clasificación:")
print(classification_report(y_test, y_pred_hot))

Mejor precisión en validación cruzada: 0.8147
Accuracy en test: 0.7757

Reporte de clasificación:
              precision    recall  f1-score   support

           0       0.80      0.83      0.82       128
           1       0.73      0.70      0.71        86

    accuracy                           0.78       214
   macro avg       0.77      0.76      0.76       214
weighted avg       0.77      0.78      0.77       214

Para mostrar codificación de categorías y extraer el OneHotEncoder entrenado, procedemos de la siguiente manera

# Extraer OneHotEncoder entrenado
ohe = grid_search.best_estimator_.named_steps["preprocessing"].named_transformers_["cat"]

# Obtener nombres de columnas después del OneHotEncoder
cat_feature_names = ohe.get_feature_names_out(categorical_cols)

# Combinar con nombres de columnas numéricas
final_feature_names = list(cat_feature_names) + numerical_cols

print("\nNombres finales de las columnas después de codificación:")
print(final_feature_names)

# Mostrar un dataframe transformado
X_train_transformed = grid_search.best_estimator_.named_steps["preprocessing"].transform(X_train)
df_transformed = pd.DataFrame(X_train_transformed, columns=final_feature_names)

print("\nPrimeras filas de X_train ya transformado:")
print(df_transformed.head())

Nombres finales de las columnas después de codificación:
['Sex_male', 'Embarked_Q', 'Embarked_S', 'Pclass_2', 'Pclass_3', 'Age', 'SibSp', 'Parch', 'Fare']

Primeras filas de X_train ya transformado:
   Sex_male  Embarked_Q  Embarked_S  Pclass_2  Pclass_3       Age     SibSp  \
0       1.0         0.0         1.0       1.0       0.0 -0.829469 -0.559914   
1       0.0         0.0         0.0       0.0       0.0 -0.413098 -0.559914   
2       0.0         0.0         0.0       0.0       1.0 -2.026536  1.716308   
3       1.0         0.0         1.0       0.0       0.0  1.078899 -0.559914   
4       1.0         0.0         1.0       0.0       1.0  0.211459 -0.559914   

      Parch      Fare  
0 -0.497747 -0.419331  
1 -0.497747  0.859891  
2  0.711414 -0.280832  
3 -0.497747 -0.115852  
4 -0.497747 -0.455035  

4.3. Codificación de Variables Categóricas#

4.3.1. Codificación de Variables Categóricas: `OneHotEncoder` vs `get_dummies` en Machine Learning#

En los modelos de Machine Learning, es común encontrarse con variables categóricas, las cuales deben transformarse en valores numéricos antes de ser utilizadas por los algoritmos de aprendizaje. Una de las estrategias más utilizadas para ello es la codificación one-hot, que convierte cada categoría en una columna binaria. scikit-learn y pandas ofrecen dos formas populares de realizar esta transformación:

OneHotEncoder (de sklearn.preprocessing)
get_dummies (de pandas)

A continuación, se describen ambos enfoques, sus diferencias y recomendaciones para su uso en el contexto de validación cruzada y pipelines.

4.3.1.1. `pd.get_dummies()`#

Es una función de pandas que convierte variables categóricas en columnas binarias (dummy variables).
Por cada categoría única, crea una nueva columna con 0 o 1 indicando la presencia de esa categoría.
Devuelve un DataFrame listo para usar.

import pandas as pd

df = pd.DataFrame({
    'Color': ['Rojo', 'Azul', 'Verde']
})

dummies = pd.get_dummies(df, columns=['Color'], dtype=int)
print(dummies)

   Color_Azul  Color_Rojo  Color_Verde
         0           1            0
         1           0            0
         0           0            1

Características clave:

Rápido y simple.
No guarda información de codificación para aplicar a datos futuros.
Devuelve columnas independientes, no un solo vector.

4.3.1.2. `OneHotEncoder`#

Es un transformador que convierte categorías en vectores binarios pero mantiene la información de mapeo.
Ideal para usar en pipelines, ya que:
- Aprende el mapeo de categorías durante el .fit().
- Puede aplicarse a nuevos datos con .transform() manteniendo el mismo orden de columnas.
Devuelve un array NumPy o una matriz dispersa (no un DataFrame) — aunque se puede convertir después.

from sklearn.preprocessing import OneHotEncoder

ohe = OneHotEncoder(sparse=False)
X = [['Rojo'], ['Azul'], ['Verde']]
ohe.fit_transform(X)

array([[0., 1., 0.],
       [1., 0., 0.],
       [0., 0., 1.]])

Características clave:

Guarda el orden y posición de cada categoría (ohe.categories_).
Maneja categorías desconocidas con handle_unknown='ignore'.
- Eso de handle_unknown='ignore' aparece como parámetro en OneHotEncoder de scikit-learn, y básicamente sirve para evitar que tu código explote cuando, en datos nuevos, aparezca una categoría que no estaba presente en el conjunto de entrenamiento.

from sklearn.preprocessing import OneHotEncoder

# Ejemplo SIN handle_unknown='ignore'
print("=== SIN handle_unknown='ignore' ===")
try:
    encoder = OneHotEncoder()
    encoder.fit([['Rojo'], ['Azul'], ['Verde']])
    print("Codificación Rojo:", encoder.transform([['Rojo']]).toarray())
    print("Codificación Amarillo:", encoder.transform([['Amarillo']]).toarray())
except Exception as e:
    print("Error:", e)

print("\n=== CON handle_unknown='ignore' ===")
# Ejemplo CON handle_unknown='ignore'
encoder = OneHotEncoder(handle_unknown='ignore')
encoder.fit([['Rojo'], ['Azul'], ['Verde']])
print("Codificación Rojo:", encoder.transform([['Rojo']]).toarray())
print("Codificación Amarillo:", encoder.transform([['Amarillo']]).toarray())

=== SIN handle_unknown='ignore' ===
Codificación Rojo: [[0. 1. 0.]]
Error: Found unknown categories ['Amarillo'] in column 0 during transform

=== CON handle_unknown='ignore' ===
Codificación Rojo: [[0. 1. 0.]]
Codificación Amarillo: [[0. 0. 0.]]

Se integra perfectamente en pipelines con escalado, imputación, modelos, etc.

Conclusión

pd.get_dummies() es rápido para exploración y pruebas, pero no apto para producción si necesitas transformar nuevos datos.
OneHotEncoder es mejor para proyectos reales o cuando trabajas con train/test split o producción, ya que mantiene consistencia en el número y orden de columnas.

4.3.2. Ejemplo Básico con `Pipeline`#

from sklearn.pipeline import Pipeline
from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import OneHotEncoder, StandardScaler
from sklearn.ensemble import RandomForestClassifier

# Variables numéricas y categóricas
num_vars = ['Age', 'Fare']
cat_vars = ['Sex', 'Embarked']

# Preprocesamiento
preprocessor = ColumnTransformer(
    transformers=[
        ('num', StandardScaler(), num_vars),
        ('cat', OneHotEncoder(handle_unknown='ignore'), cat_vars)
    ]
)

# Pipeline completo
pipeline = Pipeline(steps=[
    ('preprocessing', preprocessor),
    ('classifier', RandomForestClassifier())
])

Observación

Si en OneHotEncoder el conjunto de test tiene menos categorías que el train, no pasa nada “malo” siempre y cuando el encoder que uses para transformar el test sea el mismo que fue ajustado con el train (fit en train, transform en test).
Si en el test aparecen categorías que no estaban en el train, OneHotEncoder con handle_unknown=’ignore’ las representará como un vector de ceros, evitando que el pipeline falle. Para mitigar este problema, conviene preprocesar los datos antes de entrenar, agrupando categorías poco frecuentes en una clase “Otros”, de modo que el modelo esté mejor preparado para casos futuros.

from sklearn.preprocessing import OneHotEncoder
import pandas as pd

train = pd.DataFrame({'Color': ['Rojo', 'Azul', 'Verde']}) #Orden aprendido en la codificación
test = pd.DataFrame({'Color': ['Azul', 'Rojo']})

ohe = OneHotEncoder(sparse=False)
ohe.fit(train[['Color']])

train_encoded = ohe.transform(train[['Color']])
test_encoded = ohe.transform(test[['Color']])

print(ohe.get_feature_names_out())
print(train_encoded)
print(test_encoded)

['Color_Azul' 'Color_Rojo' 'Color_Verde']
[[0. 1. 0.]
 [1. 0. 0.]
 [0. 0. 1.]]
[[1. 0. 0.]
 [0. 1. 0.]]

from sklearn.preprocessing import OneHotEncoder
import pandas as pd

# Datos de entrenamiento
train = pd.DataFrame({'Fruta': ['Manzana', 'Pera', 'Manzana', 'Sandía']}) #Manzana frecuencia_minima = 2

# Datos de prueba (incluye fruta nueva: 'Banano')
test = pd.DataFrame({'Fruta': ['Pera', 'Banano', 'Manzana']})

# Agrupar categorías poco frecuentes en 'Otros'
frecuencia_minima = 2
categorias_frecuentes = train['Fruta'].value_counts()[lambda x: x >= frecuencia_minima].index

train['Fruta'] = train['Fruta'].where(train['Fruta'].isin(categorias_frecuentes), 'Otros')
test['Fruta'] = test['Fruta'].where(test['Fruta'].isin(categorias_frecuentes), 'Otros')

# Codificador OneHot con manejo de categorías desconocidas
ohe = OneHotEncoder(sparse=False, handle_unknown='ignore')
ohe.fit(train[['Fruta']])

# Transformar
train_encoded = ohe.transform(train[['Fruta']])
test_encoded = ohe.transform(test[['Fruta']])

# Resultados
print("Categorías aprendidas:", ohe.get_feature_names_out())
print("\nTrain codificado:\n", train_encoded)
print("\nTest codificado:\n", test_encoded)

Categorías aprendidas: ['Fruta_Manzana' 'Fruta_Otros']

Train codificado:
 [[1. 0.]
 [0. 1.]
 [1. 0.]
 [0. 1.]]

Test codificado:
 [[0. 1.]
 [0. 1.]
 [1. 0.]]

4.3.3. `OneHotEncoder` con GPU#

from numpy import array
from sklearn.preprocessing import LabelEncoder
from numpy import argmax
import tensorflow as tf

2025-08-08 22:56:23.148574: I tensorflow/core/util/port.cc:113] oneDNN custom operations are on. You may see slightly different numerical results due to floating-point round-off errors from different computation orders. To turn them off, set the environment variable `TF_ENABLE_ONEDNN_OPTS=0`.
2025-08-08 22:56:23.174977: E external/local_xla/xla/stream_executor/cuda/cuda_dnn.cc:9261] Unable to register cuDNN factory: Attempting to register factory for plugin cuDNN when one has already been registered
2025-08-08 22:56:23.175006: E external/local_xla/xla/stream_executor/cuda/cuda_fft.cc:607] Unable to register cuFFT factory: Attempting to register factory for plugin cuFFT when one has already been registered
2025-08-08 22:56:23.176221: E external/local_xla/xla/stream_executor/cuda/cuda_blas.cc:1515] Unable to register cuBLAS factory: Attempting to register factory for plugin cuBLAS when one has already been registered
2025-08-08 22:56:23.181693: I tensorflow/core/platform/cpu_feature_guard.cc:182] This TensorFlow binary is optimized to use available CPU instructions in performance-critical operations.
To enable the following instructions: AVX2 AVX512F AVX512_VNNI AVX512_BF16 FMA, in other operations, rebuild TensorFlow with the appropriate compiler flags.
2025-08-08 22:56:24.898497: W tensorflow/compiler/tf2tensorrt/utils/py_utils.cc:38] TF-TRT Warning: Could not find TensorRT

df = pd.DataFrame({'label': ['Label1', 'Label4', 'Label2', 'Label2', 'Label1', 'Label3', 'Label3']})
df

	label
0	Label1
1	Label4
2	Label2
3	Label2
4	Label1
5	Label3
6	Label3

le = LabelEncoder()
integer_encoded = le.fit_transform(df.values)
print(integer_encoded)

[0 3 1 1 0 2 2]

encoded = tf.keras.utils.to_categorical(integer_encoded)
print(encoded)

[[1. 0. 0. 0.]
 [0. 0. 0. 1.]
 [0. 1. 0. 0.]
 [0. 1. 0. 0.]
 [1. 0. 0. 0.]
 [0. 0. 1. 0.]
 [0. 0. 1. 0.]]

import numpy as np
inverted = np.argmax(encoded, axis=1)
print(inverted)

[0 3 1 1 0 2 2]

le.inverse_transform(inverted)

array(['Label1', 'Label4', 'Label2', 'Label2', 'Label1', 'Label3',
       'Label3'], dtype=object)

Observaciones

A partir del gráfico KDE de Age, se observa una distribución aproximadamente normal, lo que sugiere que el modelo GaussianNB podría ser adecuado. Este se emplea principalmente con datos de alta dimensión, mientras que MultinomialNB y BernoulliNB son más comunes en datos de texto dispersos. Entre ellos, MultinomialNB suele superar a BernoulliNB cuando hay muchas características no nulas.
Los modelos bayesianos, al igual que los modelos lineales, destacan por su rapidez en entrenamiento y predicción, facilidad de interpretación y buen rendimiento con datos dispersos de alta dimensión. Además, son robustos a los hiperparámetros y resultan especialmente útiles en conjuntos de datos muy grandes, donde entrenar modelos más complejos puede ser computacionalmente costoso.

4.4. Proyecto Integrador de Aprendizaje Automático#

4.4.1. Clasificación de enfermedades cardíacas con modelos bayesianos#

4.4.1.1. Objetivo general#

Aplicar un modelo supervisado de clasificación basado en la probabilidad bayesiana (GaussianNB) para predecir la presencia o ausencia de enfermedad cardíaca en pacientes a partir de indicadores clínicos. El objetivo es:

Construir un pipeline de preprocesamiento y clasificación usando GaussianNB.
Evaluar el desempeño del modelo usando métricas estándar y visualizaciones.
Analizar el impacto de cada variable en la predicción desde la perspectiva probabilística.

4.4.1.2. Contexto aplicado#

Los sistemas de salud buscan modelos interpretables para apoyar el diagnóstico temprano de enfermedades. Uno de los problemas más frecuentes es el diagnóstico de enfermedad cardíaca, donde se tienen múltiples mediciones clínicas, y se requiere estimar el riesgo de forma transparente. Los clasificadores bayesianos son una herramienta adecuada por su rapidez, simplicidad e interpretabilidad.

4.4.1.3. Dataset sugerido#

Heart Disease UCI Dataset

Fuente: UCI Machine Learning Repository
Registros: 303 pacientes
Enlace: https://archive.ics.uci.edu/ml/datasets/Heart+Disease

4.4.1.4. Variables disponibles (ejemplo)#

Tipo	Variables principales
Demográficas	Edad, sexo
Clínicas	Presión arterial, colesterol, frecuencia cardíaca máxima
Síntomas	Dolor torácico, angina inducida por ejercicio, nivel de azúcar en sangre
Diagnóstico	`target` (1 = enfermedad presente, 0 = ausencia de enfermedad)

4.4.1.5. Tareas#

Preprocesamiento
- Limpieza de valores faltantes o codificación de valores especiales
- Codificación de variables categóricas (ChestPain, Thal, etc.)
- Escalado si se combina con otras técnicas comparativas
- División de datos con train_test_split
Modelado
- Implementar un Pipeline con preprocesamiento y GaussianNB
- (Opcional) Comparar con BernoulliNB o MultinomialNB si hay discretización
- Realizar validación cruzada para estimar la robustez del clasificador
Evaluación
- Métricas: matriz de confusión, accuracy, precision, recall, F1-score
- Curva ROC y cálculo de AUC
- Gráficos de distribución de predicciones y probabilidad condicional
- Comparar desempeño con otros clasificadores si se desea (por ejemplo LogisticRegression)
Análisis y reporte
- Analizar cuáles variables son más relevantes según su efecto en las probabilidades
- Discutir fortalezas y limitaciones del modelo bayesiano (asunción de independencia)
- Reflexión sobre interpretabilidad y aplicabilidad médica

4.4.1.6. Restricciones didácticas#

Se debe usar Pipeline de scikit-learn
No se permite el uso de GridSearchCV (ya que GaussianNB no tiene hiperparámetros principales)
El trabajo debe estar documentado, reproducible y visualmente explicado
Se debe justificar el uso del modelo bayesiano en el contexto médico

4.4.1.7. Herramientas sugeridas#

pandas, numpy, scikit-learn
matplotlib, seaborn
Jupyter Notebook o Google Colab

4.4.1.8. Resultado esperado#

Un cuaderno de trabajo completo que incluya:

Preprocesamiento y exploración de los datos
Implementación del clasificador bayesiano con Pipeline
Evaluación del modelo con métricas apropiadas
Análisis crítico de resultados y visualizaciones
Conclusiones orientadas a aplicaciones médicas o clínicas

4.4.1.9. Diseño sugerido del notebook#

Carga y análisis exploratorio del dataset
Preprocesamiento y codificación
Definición del pipeline con GaussianNB
Evaluación de resultados y visualizaciones
Reflexión crítica y conclusiones

4.4.1.10. Resumen#

Dataset	Tarea	Tamaño	Ventajas clave
UCI Heart Disease	Clasificación	303	Real, médico, ideal para modelos interpretables