14. Apéndice

• En este apéndice, resumimos algunas definiciones y teoremas básicos sobre los espacios de Hilbert y el análisis convexo. No se proporcionan pruebas, el lector interesado puede consultar libros más especializados, que se indican en las referencias.

Definition 14.1 (Espacios lineales)

Un conjunto no vacío de elementos, \(V\), se llama espacio lineal si hay definidas dos operaciones, adición y multiplicación escalar, de modo que se cumplen las siguientes propiedades:

• \(\boldsymbol{x}+\boldsymbol{y}=\boldsymbol{y}+\boldsymbol{x},\quad\forall\,\boldsymbol{x},\boldsymbol{y}\in V\)

• \((\boldsymbol{x}+\boldsymbol{y})+\boldsymbol{z}=\boldsymbol{x}+(\boldsymbol{y}+\boldsymbol{z}),\quad\forall~\boldsymbol{x}, \boldsymbol{y}, \boldsymbol{z}\in V\)

• Existe un elemento \(\boldsymbol{0}\in V\), conocido como el vector cero, tal que, \(\forall\boldsymbol{x}\in V,~\boldsymbol{x}+\boldsymbol{0}=\boldsymbol{x}\)

• \(\forall~x\in V\), existe un \(\boldsymbol{y}\in V\) tal que \(\boldsymbol{x}+\boldsymbol{y}=0\).

• Para cada par de escalares \(\alpha, \beta\in\mathbb{C}\) y \(\forall~\boldsymbol{x},\boldsymbol{y}\in V\),

\[(\alpha\beta)\boldsymbol{x}=\alpha(\beta\boldsymbol{x})\quad\text{y}\quad\alpha(\boldsymbol{x}+\boldsymbol{y})=\alpha\boldsymbol{x}+\alpha\boldsymbol{y}.\]

• Para cada par de escalares \(\alpha,\beta\in\mathbb{C},~\forall~\boldsymbol{x}\in V,\quad (\alpha+\beta)\boldsymbol{x}=\alpha\boldsymbol{x}+\beta\boldsymbol{x}\)

• \(\forall\boldsymbol{x}\in V\), y el escalar \(1\in\mathbb{C},\quad 1\boldsymbol{x}=\boldsymbol{x}\)

• Los espacios lineales se denominan a veces espacios vectoriales y los elementos de \(V\) vectores. Si los escalares \(\alpha, \beta\) están restringidos en \(\mathbb{R}\), entonces el espacio lineal se conoce como espacio lineal real; de lo contrario, si \(\alpha, \beta \in\mathbb{C}\), el espacio lineal se conoce como espacio lineal complejo.

Example 14.1 (El espacio vectorial \(\mathbb{R}^{l}\))

El conjunto de \(l-\)tuplas \(\boldsymbol{x}:=(x_{1}, x_{2},\dots, x_{l}),~x_{i}\in\mathbb{R},~i=1,2,\dots,l\), es un espacio vectorial real, donde la adición y la multiplicación están definidas como

\[\begin{split}\begin{align} \boldsymbol{x}+\boldsymbol{y}&=(x_{1}+y_{1}, x_{2}+y_{2},\dots,x_{l}+y_{l})\\ a\boldsymbol{x}&=(ax_{1}, ax_{2},\dots, ax_{l}),\quad a\in\mathbb{R}. \end{align}\end{split}\]

Example 14.2

Sea el conjunto de todas las funciones reales

\[\mathcal{F}=\{\boldsymbol{f}:=f(x) | f:\mathbb{R}\longrightarrow\mathbb{R}\},\]

donde \(\boldsymbol{f}\) denota la función general, en vez de la evaluación en un punto especifico \(x\in\mathbb{R}\). Entonces \(\mathcal{F}(\mathbb{R})\) es un espacio lineal real con respecto a las siguientes operaciones

\[\begin{split}\begin{align} (\boldsymbol{f}+\boldsymbol{h})(x)&=f(x)+h(x),\quad\forall~\boldsymbol{f},\boldsymbol{g}\in\mathcal{F}(\mathbb{R}),\\ (a\boldsymbol{f})(x)&=af(x),\quad\forall~\boldsymbol{f}\in\mathcal{F}(\mathbb{R}),~a\in\mathbb{R}. \end{align}\end{split}\]

Definition 14.2

Sea \(V\) un espacio lineal y \(S\) un conjunto no vacio, \(S\subseteq V\). Entonces \(S\) es llamado un subespacio de \(V\) si

• \(\forall\boldsymbol{x}, \boldsymbol{y}\in S,\quad \boldsymbol{x}+\boldsymbol{y}\in S\)

• \(\forall a\in\mathbb{C}\), y \(\boldsymbol{x}\in S,~a\boldsymbol{x}\in S\)

Definition 14.3 (Independencia Lineal)

Sea \(V\) un subespacio lineal y \(S\subseteq V\). Decimo que \(S\) es linealmente independiente si existe un número finito de elementos distintos, \(x_{k}\in S,~i=1,2,\dots,K\), tal que

\[\sum_{k=1}^{K}a_{k}\boldsymbol{x}_{k}=\boldsymbol{0}\]

para alguna combinación de escalares \(a_{k}\in\mathbb{C},~k=1,2,\dots,K\), los cuales no son todos ceros. Si este no es el caso, el conjunto \(S\) es linealmente independiente

Definition 14.4 (Subespacio generado)

Sea \(S\) un subconjunto no vacio \(S\subseteq V\). El conjunto de todas las combinaciones lineales posibles, denotado como \(\text{span}\{S\}\),

\[ \text{span}\{S\}=\left\{\boldsymbol{x}:~\boldsymbol{x}=\sum_{i=1}^{K}a_{k}\boldsymbol{x}_{k}|x_{k}\in S,~K\in\mathbb{N}\right\} \]

y es conocido como el \(\textbf{generado}\) de \(S\). Note que \(\text{span}\{S\}\) es siempre un subespacio de \(V\). Además si \(\text{span}\{S\}=V\), decimos que \(S\) genera al espacio \(V\).

Definition 14.5 (Bases)

Sea \(V\) un subespacio lineal y \(S\subseteq V\). El conjunto \(S\) es conocido como base de \(V\), si y solo si:

• \(S\) es linealmente independiente

• \(S\) genera a \(V\)

• Si el número de elementos que componen \(S\) es finito, decimos que \(V\) es de dimensión finita y el número de elementos distintos de S define la dimensión de \(V\). Si el número de elementos de \(S\) no es finito, decimos que \(V\) es de dimensión infinita.

• Nótese que no hay una base única en \(V\). Sin embargo, cualquier base de \(V\) tiene el mismo número de elementos. Además, se ha demostrado que todo espacio lineal tiene una base. Esto se conoce como el Lema de Zorn. Sin embargo, encontrar una base no es necesariamente una tarea trivial. La dimensión de \(\mathbb{R}^{l}\) es \(l\), y el espacio lineal \(\mathcal{F}(\mathbb{R})\) es de dimensión infinita.

Espacio vectorial de polinomios en \(x\) con coeficientes racionales

• Sea \(P\) el espacio vectorial de todos los polinomios en \(x\) con coeficientes racionales, con la adición de polinomios habitual como suma de vectores y la multiplicación de un polinomio por un número racional como multiplicación por escalar. Afirmamos que \(P\) es de dimensión infinita.

• En efecto. Supongamos, por el contrario, que \(P\) es generado por \(k\) polinomios en \(P\), \(\{p_{1}, p_{2},\dots,p_{k}\}\). Sea \(m\) el máximo de los grados de estos \(k\) polinomios.

• Entonces \(x^{m+1}\) es un vector en \(P\), pero no puede ser escrito como una combinación lineal de \(\{p_{1}, p_{2}, \dots, p_{k}\}\) porque tomar combinaciones lineales de polinomios de grado como máximo \(m\) no puede dar polinomios de grado mayor que \(m\).

• Por lo tanto, \(x\) no está en el generado de \(\{p_{1}, p_{2},\dots,p_{k}\}\), lo cual es una contradicción.

Definition 14.6 (Espacio con producto interno)

Sea \(V\) un espacio lineal. El producto interno es una función

\[f:V\times V\longmapsto\mathbb{C}\]

la cual asigna un valor en \(\mathbb{C}\), denotado \(\langle\boldsymbol{x}, \boldsymbol{y}\rangle\), para cada punto de elementos \(\boldsymbol{x}, \boldsymbol{y}\in V\), con las siguientes propiedades:

• \(\langle\boldsymbol{x}, \boldsymbol{y}\rangle\geq0\), y \(\langle\boldsymbol{x}, \boldsymbol{y}\rangle=0\) si y solo si \(\boldsymbol{x}=0\)

• \(\langle\boldsymbol{x}+\boldsymbol{y}, \boldsymbol{z}\rangle=\langle\boldsymbol{x}, \boldsymbol{z}\rangle+\langle\boldsymbol{y}, \boldsymbol{z}\rangle\)

• \(\langle a\boldsymbol{x}, \boldsymbol{y}\rangle=a\langle\boldsymbol{x}, \boldsymbol{y}\rangle\)

• \(\langle\boldsymbol{x}, \boldsymbol{y}\rangle=\langle\boldsymbol{y}, \boldsymbol{x}\rangle^{\star}\)

donde \(\star\) denota la conjugación compleja. Un espacio donde un producto interno a sido definido es conocido como un espacio con producto interno.

Definition 14.7

Consideremos el espacio vectorial \(\mathbb{C}^{l}\). Entonces la operación

\[\langle\boldsymbol{x}, \boldsymbol{y}\rangle:=\sum_{i=1}^{l}x_{i}y_{i}^{\star}=\boldsymbol{y}^{H}\boldsymbol{x},\]

es un producto interno con \(\boldsymbol{x}, \boldsymbol{y}\in\mathbb{C}^{l}\).

Definition 14.8 (Norma y espacios normados)

Sea \(V\) un espacio lineal. Una norma es una función

\[f:V\longmapsto[0,\infty),\]

que asigna un número real positivo a cada \(\boldsymbol{x}\in V\), esta es denotada como \(\|\boldsymbol{x}\|\) y tiene las siguientes propiedades

• \(\|\boldsymbol{x}\|\geq0,\quad\) \(\|\boldsymbol{x}\|=0\quad\text{sii}\quad\boldsymbol{x}=\boldsymbol{0}\)

• \(\|a\boldsymbol{x}\|=|a|\|\boldsymbol{x}\|,\quad\forall a\in\mathbb{C},\quad\text{y}\quad\boldsymbol{x}\in V\)

• \(\|\boldsymbol{x}+\boldsymbol{y}\|\leq\|\boldsymbol{x}\|+\|\boldsymbol{y}\|,\quad\forall\boldsymbol{x}, \boldsymbol{y}\in V\).

Dado un espacio lineal, podemos definir diferentes normas. Por ejemplo, el espacio vectorial \(\mathbb{C}^{l}\). Entonces definimos la norma \(l_{p}\) como

\[ \|\boldsymbol{x}\|_{p}=\left(\sum_{i=1}^{l}|x_{i}|^{p}\right)^{1/p},\quad p\geq1 \]

Se puede demostrar que la definición anterior cumple con todas las propiedades requeridas para que una función sea una norma. Para \(p = 1\), nos referimos a la norma \(l_{1}\) y para \(p = 2\) se conoce como \textbf{norma euclidiana} o norma \(l_{2}\). Nótese que esta última resulta de la operación de producto interior, es decir,

(14.1)\[ \|\boldsymbol{x}\|_{2}=\sqrt{\boldsymbol{x}^{H}\boldsymbol{x}}. \]

Esto es válido para cualquier espacio lineal de producto interno. Es decir, dado un espacio lineal con producto interno, \(V\), con \(\langle\cdot,\cdot\rangle\), entonces la operación de producto interior induce una norma, es decir

\[ \|\boldsymbol{x}\|=\langle\boldsymbol{x}, \boldsymbol{x}\rangle,\quad\boldsymbol{x}\in V. \]

Theorem 14.1 (Desigualdad de Cauchy-Schwarz)

Sea \(V\) un espacio de producto interno y el reproductor por la norma del producto interior. Entonces

\[|\langle\boldsymbol{x}, \boldsymbol{y}\rangle|\leq\|\boldsymbol{x}\|\boldsymbol{y}\|,\quad\boldsymbol{x}, \boldsymbol{y}\in V:\quad\text{Desigualdad de Cauchy-Schwarz}.\]

Esta es una de las propiedades más fundamentales e importantes en la teoría de los espacios lineales. Una consecuencia directa de la desigualdad de Cauchy-Schwarz son las siguientes propiedades: Dado un espacio vectorial interior y su norma inducida \(\|\boldsymbol{x}\|\), entonces

• \(\left|\|\boldsymbol{x}\|-\|\boldsymbol{y}\|\right|\leq\|\boldsymbol{x}-\boldsymbol{y}\|\)

• \(\|\boldsymbol{x}+\boldsymbol{y}\|^{2}+\|\boldsymbol{x}-\boldsymbol{y}\|=2\left(\|\boldsymbol{x}\|^{2}+\|\boldsymbol{y}\|^{2}\right)\).

Esta última se conoce como la ley del paralelogramo. Nótese que, todas estas propiedades, que pueden conocerse a partir de la geometría básica, son válidas para cualquier espacio lineal, incluso para los de dimensión infinita.

Example 14.3 (El espacio \(l^{2}\))

Este es el espacio lineal de todas las sucesiones

\[\boldsymbol{x}=(x_{1}, x_{2},\dots,x_{n},\dots),\]

con producto interno

\[\langle\boldsymbol{x}, \boldsymbol{y}\rangle=\sum_{n=1}^{\infty}x_{n}y_{n}^{\star},\]

el cual induce la norma que satisface la siguiente propiedad

\[\|\boldsymbol{x}\|:=\sqrt{\sum_{n=1}^{\infty}|x_{n}|^{2}}<\infty\]

Example 14.4 (El espacio \(L^{2}\))

Este es el espacio lineal de todas las funciones integrables

\[f:\mathbb{R}\mapsto\mathbb{R},\]

con producto interno

\[\langle\boldsymbol{f}, \boldsymbol{h}\rangle:=\int_{-\infty}^{\infty}f(x)h(x)dx,\]

el cual induce la norma que satisface la propiedad

\[\|\boldsymbol{f}\|:=\sqrt{\int_{-\infty}^{\infty}|f(x)|^{2}dx}<+\infty.\]

Definition 14.9 (Convergencia, Sucesiones de Cauchy y Espacios Completos)

Sea \(V\) un espacio lineal normado y sea \(\boldsymbol{x}_{1}, \boldsymbol{x}_{2},\dots,\boldsymbol{x}_{n},\dots\) una sucesión de elementos en \(V\). Decimos que la sucesión converge a \(\boldsymbol{x}\) si

\[\lim_{n\rightarrow\infty}\|\boldsymbol{x}_{n}-\boldsymbol{x}\|=0.\]

Nótese que si \(\boldsymbol{x}\) existe, este es único y es conocido como el límite de \(\boldsymbol{x}_{n}\).

Una sucesión de elementos en un espacio lineal normado \(V\) es llamada una sucesión de Cauchy si esta satisface

\[\lim_{n, m\rightarrow\infty}\|\boldsymbol{x}_{n}-\boldsymbol{x}_{m}\|=0.\]

En otras palabras, la norma de la diferencia de cualquier par de elementos en la sucesión tiende a cero. Se puede demostrar que toda sucesión convergente es de Cauchy, el sentido contrario de esta afirmación no siempre es cierto.

Un espacio lineal normado \(V\), en el que cada sucesión de Cauchy converge en \(V\) se dice que es completo. Nótese que cualquier espacio lineal de dimensión finita es completo. Sin embargo, esto no es siempre verdadero para espacios de dimensión infinita.

Definition 14.10 (Espacios de Hilbert)

Un espacio con producto interno, el cual es completo con respecto a la norma inducida por el producto interno es llamado un espacio de Hilbert.

Ejemplos de espacios de Hilbert son \(l^{2}\) y \(L^{2}\). También los espacios vectoriales \(\mathbb{C}^{l}\) y \(\mathbb{R}^{l}\), equipados con la operación de producto interno Definition 14.7 y la norma Euclideana definida por (14.1), conocidos como espacios Euclidianos son casos especiales de espacios de Hilbert de dimensión finita. Los espacios \(l^{2}\) y \(L^{2}\) son de dimensión infinita. Nótese que \(\mathbb{C}^{l}\), equipado con la norma \(l_{p},~ p\neq2\), no es un espacio de Hilbert, debido a que esta norma no es inducida por un producto interno.

Definition 14.11 (Subsespacio cerrado)

Sea \(H\) un espacio de Hilbert y \(S\subseteq H\). Decimos que \(S\) es un subespacio cerrado de \(H\), si para toda \(\{x_{n}\}\subseteq S\), esto es, cualquier sucesión de elementos de \(S\), que converge a un elemento \(x\in H\), se tiene que \(x\in S\).

Theorem 14.2

Sea \(H\) un espacio de Hilbert y \(\varphi_{1}, \varphi_{2},\dots, \varphi_{m}\in H\) donde \(m<\infty\). Entonces el espacio lineal generado \(\text{span}\{\varphi_{1}, \varphi_{2},\dots, \varphi_{m}\}\) es un subespacio cerrado de \(H\).

Definition 14.12

Sea \(A\) un subconjunto no vacio de un espacio de Hilbert \(H\). Entonces, el conjunto de todos los vectores ortogonales a \(A\), dentoado por \(A^{\perp}\), es llamado el complemento ortogonal de \(A\) y se define de las siguiente manera

\[ A^{\perp}=\{x\in H:~\langle x, y\rangle=0,~\forall~y\in A\}. \]

Theorem 14.3 (Descomposición ortogonal)

Si \(M\) es un subespacio cerrado de un espacio de Hilbert \(H\), entonces

\[ H=M\oplus M^{T}. \]

Definition 14.13

Un subconjunto no vacio \(C\) de un espacio de Hilbert \(H\), esto es \(C\subseteq H\), es llamado convexo, si \(\forall~\boldsymbol{x}_{1}, \boldsymbol{x}_{2}\in C\) y \(\forall\lambda\in [0,1]\) se tiene que

(14.2)\[ \boldsymbol{x}:=\lambda\boldsymbol{x}_{1}+(1-\lambda)\boldsymbol{x}_{2}\in C \]

• Nótese que si \(\lambda=1\) entonces \(\boldsymbol{x}=\boldsymbol{x}_{1}\), y si \(\lambda=0\) entonces \(\boldsymbol{x}=\boldsymbol{x}_{2}\). para cualquier otro \(\lambda\in[0, 1]\) se tiene que \(\boldsymbol{x}\) cae dentro de la línea que conecta \(\boldsymbol{x}_{1}\) con \(\boldsymbol{x}_{2}\). La ecuación (14.2) puede escribirse como

\[ \boldsymbol{x}-\boldsymbol{x}_{2}=\lambda(\boldsymbol{x}_{1}-\boldsymbol{x}_{2}),\quad 0\leq\lambda\leq1. \]

• Por ejemplo, la función \(f:\mathbb{R}\longrightarrow\mathbb{R}\) definida por \(f(x)=|x|\) es una función convexa. Observe que \(\forall x_{1}, x_{2}\in\mathbb{R}\) se tiene que

\[\begin{split} \begin{align*} f(\lambda x_{1}+(1-\lambda)x_{2})&=|\lambda x_{1}+(1-\lambda)x_{2}|\\[2mm] &\leq|\lambda x_{1}|+|(1-\lambda)x_{2}|\\[2mm] &=\lambda|x_{1}|+|1-\lambda||x_{2}|\\[2mm] &=\lambda f(x_{1})+(1-\lambda)f(x_{2}). \end{align*} \end{split}\]

Definition 14.14

Una función \(f:\mathcal{X}\subset\mathbb{R}^{l}\longrightarrow\mathbb{R}^{l}\) es llamada convexa si \(\mathcal{X}\) es convexo y si \(\forall~\boldsymbol{x}_{1}, \boldsymbol{x}_{2}\in\mathcal{X}\) se tiene que:

\[ f(\lambda\boldsymbol{x}_{1}+(1-\lambda)\boldsymbol{x}_{2})\leq\lambda f(\boldsymbol{x}_{1})+(1-\lambda)f(\boldsymbol{x}_{2}),\quad\lambda\in [0, 1]. \]

• Si la desigualdad se mantiene estrica decimos que \(f\) es estrictamente convexa. Además, en este caso el gráfico de la línea queda por encima de \(f(\boldsymbol{x})\)

Theorem 14.4

• Sea \(\mathcal{X}\subset\mathbb{R}^{l}\) convexo y \(f:\mathcal{X}\longrightarrow\mathbb{R}\) diferenciable. Entonces \(f(\cdot)\) es convexa si y solo si, \(\forall~\boldsymbol{x}, \boldsymbol{y}\in\mathcal{X}\),

(14.3)\[ f(\boldsymbol{y})\geq f(\boldsymbol{x})+\nabla^{T}f(\boldsymbol{x})(\boldsymbol{y}-\boldsymbol{x}). \]

• Decimos que el vector \(\nabla^{T}f(\boldsymbol{x})\) es el subgradiente de \(f\) en \(x\) si satisface la desigualdad (14.3).

• Esto es el grafico de la función convexa está ubicado por encima del gráfico de la función afín

  \[\begin{split} \\[1mm] g:y\longrightarrow\nabla^{T}f(\boldsymbol{x})(\boldsymbol{y}-\boldsymbol{x})+f(\boldsymbol{x}), \end{split}\]

  la cual define el hiperplano tangente a la gráfica de \(f\) en \((\boldsymbol{x}, f(\boldsymbol{x}))\).

Theorem 14.5

Sea \(\mathcal{X}\subset\mathbb{R}^{l}\) convexo. Entonces una función doblemente diferenciable \(f:\mathcal{X}\longrightarrow\mathbb{R}\), es convexa (estrictamente convexa) si y solo si la matriz Hessian es semi definida positiva (definida positiva).

• Por ejemplo considere la función cuadratica

  \[\begin{split} \\[1mm] f(\boldsymbol{x}):=\frac{1}{2}\boldsymbol{x}^{T}Q\boldsymbol{x}+\boldsymbol{b}^{T}\boldsymbol{x}+c, \end{split}\]

  donde \(Q\) es una matriz definida positiva. Nótese que el gradiente está dado por

  \[\begin{split} \\[1mm] \nabla f(\boldsymbol{x})=Q\boldsymbol{x}+\boldsymbol{b}, \end{split}\]

  y la matriz Hessiana es igual a \(Q\), la que por hipótesis es definida positiva, por lo tanto \(f\) es una función estrictamente convexa.

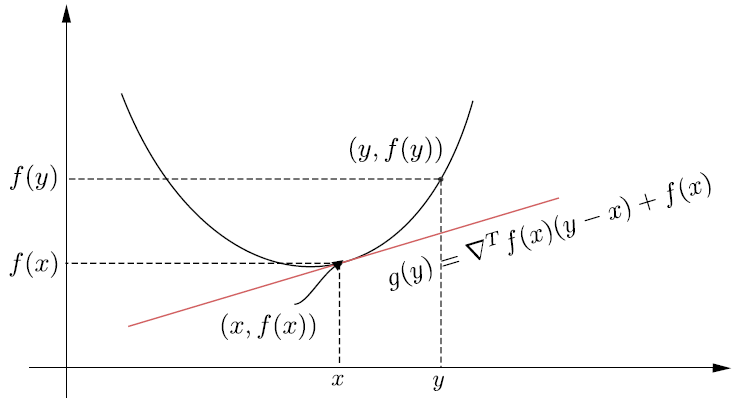
Fig. 14.1 Gráfica de una función convexa.