10. Cadenas de Algoritmos y Pipelines

• El rendimiento de los algoritmos de aprendizaje automático depende de la representación de los datos, desde el escalado hasta el aprendizaje de características no supervisadas. La mayoría de las aplicaciones requieren encadenar múltiples transformaciones y modelos.

• La clase Pipeline simplifica este proceso, permitiendo combinar pasos de preprocesamiento y modelos en un solo flujo. Además, Pipeline puede integrarse con GridSearchCV para optimizar todos los parámetros a la vez. Un ejemplo muestra que el uso de MinMaxScaler mejora significativamente el desempeño de un SVM en el conjunto de datos cancer.

import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import roc_auc_score

np.random.seed(0)
n = 1000
X = np.random.rand(n, 5)
y = np.random.randint(0, 2, size=n)

leaky_feature = y + np.random.normal(0, 0.001, size=n)
X_with_leak = np.hstack([X, leaky_feature.reshape(-1, 1)])

• Primer intento usando el modelo de clasificación LogisticRegression()

scaler = StandardScaler().fit(X_with_leak)
X_scaled = scaler.transform(X_with_leak)

X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.3, random_state=42)

model = LogisticRegression()
model.fit(X_train, y_train)

y_scores = model.predict_proba(X_test)[:, 1]
print("AUC con data leakage: {:.3f}".format(roc_auc_score(y_test, y_scores)))

AUC con data leakage: 1.000

• Segundo intento usando el modelo de clasificación LogisticRegression()

X_clean = X
X_train, X_test, y_train, y_test = train_test_split(X_clean, y, test_size=0.3, random_state=42)

scaler = StandardScaler().fit(X_train)
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)

model = LogisticRegression()
model.fit(X_train_scaled, y_train)

y_scores = model.predict_proba(X_test_scaled)[:, 1]
print("AUC sin data leakage: {:.3f}".format(roc_auc_score(y_test, y_scores)))

AUC sin data leakage: 0.499

10.1. Selección de parámetros con preprocesamiento

• Ahora digamos que queremos encontrar mejores parámetros para el SVC usando GridSearchCV, como se ha discutido en secciones anteriores. ¿Cómo podemos hacerlo? Un enfoque ingenuo podría ser el siguiente

import numpy as np
from sklearn.svm import SVC
from sklearn.pipeline import Pipeline
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import roc_auc_score

np.random.seed(0)
n = 1000
X = np.random.rand(n, 5)
y = np.random.randint(0, 2, size=n)

leaky_feature = y + np.random.normal(0, 0.001, size=n)
X_with_leak = np.hstack([X, leaky_feature.reshape(-1, 1)])

X_train, X_test, y_train, y_test = train_test_split(
    X_with_leak, y, test_size=0.3, random_state=42
)

scaler = MinMaxScaler().fit(X_train)
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)

param_grid = {
    'C': [0.01, 0.1, 1, 10, 100],
    'gamma': [0.01, 0.1, 1, 10, 100]
}

grid_leak = GridSearchCV(SVC(probability=True), param_grid=param_grid, cv=5, scoring="roc_auc")
grid_leak.fit(X_train_scaled, y_train)

y_scores_leak = grid_leak.predict_proba(X_test_scaled)[:, 1]
auc_leak = roc_auc_score(y_test, y_scores_leak)

print("AUC con data leakage (sin pipeline): {:.3f}".format(auc_leak))
print("Mejores parámetros (con leakage):", grid_leak.best_params_)

AUC con data leakage (sin pipeline): 1.000
Mejores parámetros (con leakage): {'C': 0.01, 'gamma': 0.01}

• Se realiza una búsqueda en red (grid-search) sobre los parámetros de SVC utilizando los datos escalados. Al escalar, se usa todo el conjunto de entrenamiento, y los datos escalados se emplean en la búsqueda en red con validación cruzada (cv=5). En cada división, una parte del conjunto de entrenamiento se usa para entrenar y otra para evaluar, simulando cómo el modelo clasificaría nuevos datos.

• Es clave notar que, en la validación cruzada, la parte de prueba sigue perteneciendo al conjunto de entrenamiento y el escalado se calcula con todos los datos de entrenamiento. Sin embargo, en la evaluación final con datos nuevos, estos pueden tener un mínimo y un máximo diferentes, afectando el escalado. El siguiente ejemplo ilustra este proceso en la validación cruzada y la evaluación final.

import mglearn

mglearn.plots.plot_improper_processing()

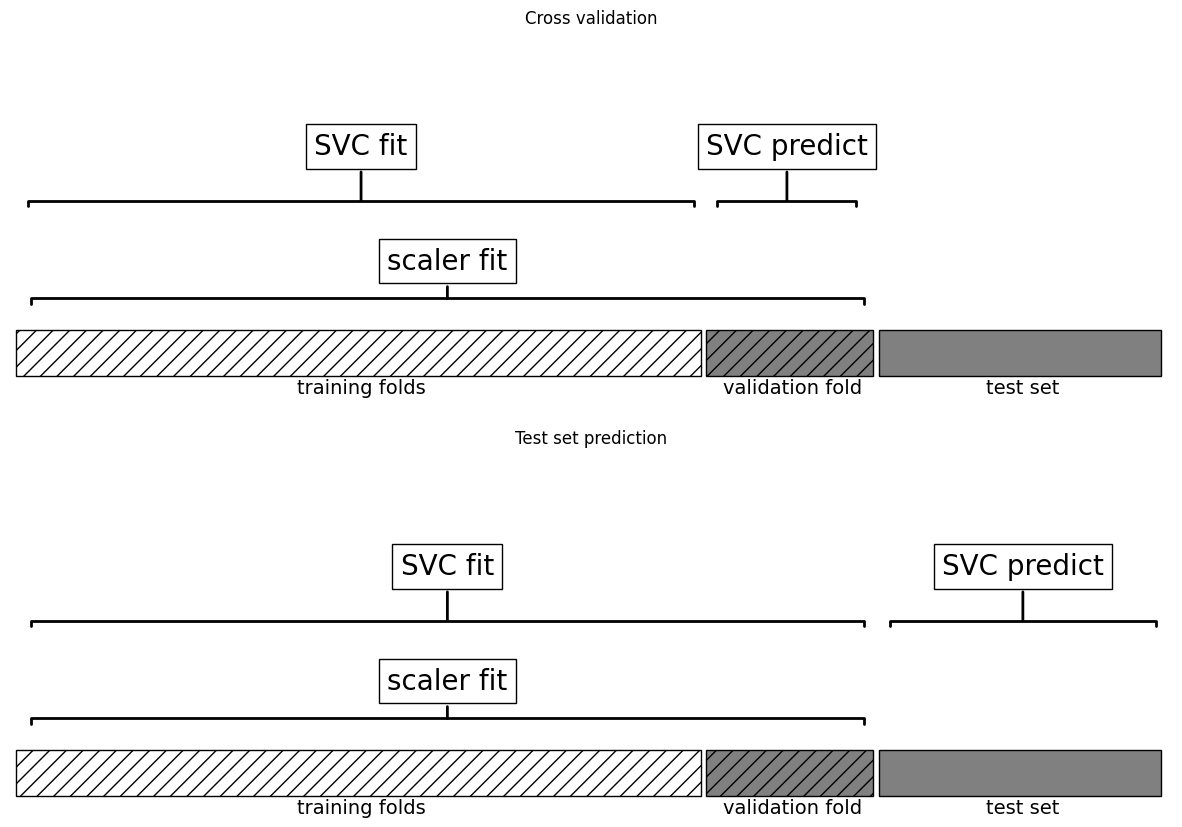
• La validación cruzada puede dar resultados demasiado optimistas si se filtra información antes de la división de los datos, lo que puede llevar a la selección de parámetros subóptimos. Para evitarlo, la división debe hacerse antes del preprocesamiento, asegurando que cualquier conocimiento extraído solo afecte el conjunto de entrenamiento. La validación cruzada debe ser el “bucle más externo” del proceso.

• En scikit-learn, esto se maneja con Pipeline, que permite combinar varios pasos de preprocesamiento y modelado en un solo estimador. Pipeline facilita el ajuste, la predicción y la evaluación, integrando transformaciones como el escalado junto con modelos supervisados.

Observacion

La fuga de datos ocurre cuando el modelo usa información ajena al conjunto de entrenamiento, afectando su evaluación. Si hay datos compartidos entre entrenamiento y prueba, los resultados pueden ser artificialmente altos, ya que el modelo ha sido expuesto previamente a los datos de prueba.

10.2. Construyendo Pipelines with GridSearch

• El impacto de la fuga de información en la validación cruzada depende del preprocesamiento. La estimación de escala en el pliegue de prueba tiene un impacto menor, pero usarlo en la extracción o selección de características puede distorsionar significativamente los resultados.

• A diferencia de la búsqueda en red que hicimos antes, ahora para cada división en la validación cruzada, el MinMaxScaler se reajusta solo con las divisiones de entrenamiento y no se filtra información de la división de prueba en la búsqueda de parámetros`

mglearn.plots.plot_proper_processing()

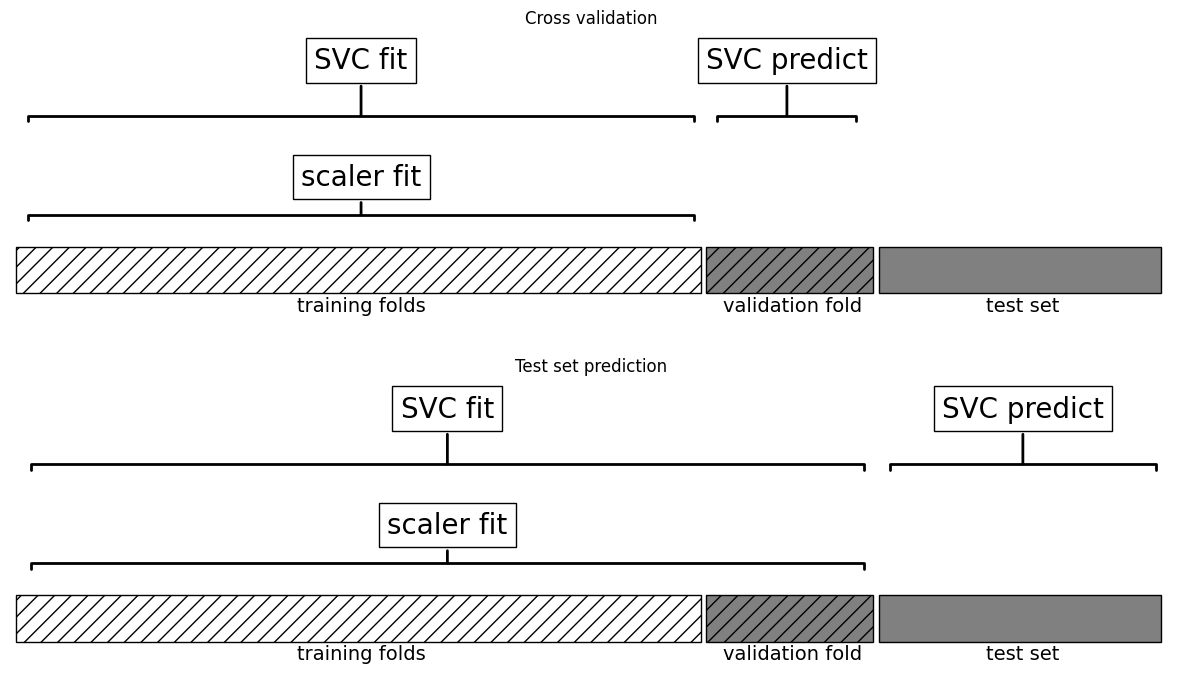
• Veamos cómo podemos utilizar la clase Pipeline para expresar el flujo de trabajo para entrenar una SVM después de escalar los datos con MinMaxScaler (por ahora sin grid-search). Primero, construimos un objeto pipeline proporcionándole una lista de pasos. Cada paso es una tupla que contiene un nombre (cualquier cadena de su elección) y una instancia de un estimador

• El uso de Pipeline en GridSearchCV es como con cualquier estimador: se define un diccionario de parámetros donde cada clave indica el paso y el parámetro usando doble guión bajo, por ejemplo, "svm__C" y "svm__gamma" si el modelo SVC se llama "svm" en el pipeline.

pipe = Pipeline([
    ("scaler", MinMaxScaler()),
    ("svm", SVC(probability=True))
])

param_grid_pipe = {
    'svm__C': [0.01, 0.1, 1, 10, 100],
    'svm__gamma': [0.01, 0.1, 1, 10, 100]
}

grid_pipe = GridSearchCV(pipe, param_grid=param_grid_pipe, cv=5, scoring="roc_auc")
grid_pipe.fit(X_train, y_train)

GridSearchCV(cv=5,
             estimator=Pipeline(steps=[('scaler', MinMaxScaler()),
                                       ('svm', SVC(probability=True))]),
             param_grid={'svm__C': [0.01, 0.1, 1, 10, 100],
                         'svm__gamma': [0.01, 0.1, 1, 10, 100]},
             scoring='roc_auc')

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

• En el paso anterior, hemos creado dos pasos: el primero, llamado "scaler", es una instancia de MinMaxScaler y el segundo, llamado "svm", es una instancia de SVC. Ahora, podemos ajustar nuestro pipeline, como cualquier otro estimador de scikit-learn.

• grid_pipe.fit primero llama a fit en el primer paso (el escalador), luego transforma los datos de entrenamiento usando el escalador, y finalmente ajusta la SVM con los datos escalados. Para evaluar en los datos de prueba, simplemente llamamos a grid_pipe.predict_proba

y_scores_pipe = grid_pipe.predict_proba(X_test)[:, 1]
auc_pipe = roc_auc_score(y_test, y_scores_pipe)

print("AUC sin data leakage (con pipeline): {:.3f}".format(auc_pipe))
print("Mejores parámetros (sin leakage):", grid_pipe.best_params_)

AUC sin data leakage (con pipeline): 0.500
Mejores parámetros (sin leakage): {'svm__C': 0.01, 'svm__gamma': 0.01}

• El impacto de la fuga de información en la validación cruzada depende del preprocesamiento. La estimación de escala en el pliegue de prueba tiene un impacto menor, pero usarlo en la extracción o selección de características puede distorsionar significativamente los resultados.

10.3. Data Leakage

• La fuga de datos (data-leakage) ocurre cuando se utiliza información no disponible en el momento de la predicción, lo que produce estimaciones optimistas y un bajo rendimiento en producción. Suele originarse por una separación incorrecta entre entrenamiento y prueba, permitiendo que el modelo acceda, directa o indirectamente, a datos reservados.

• Las transformaciones de preprocesamiento, como la normalización o la selección de características, deben ajustarse exclusivamente con los datos de entrenamiento; incluir los de prueba introduce sesgo. Esta situación se ilustrará mediante un problema de clasificación binaria con 10,000 características aleatorias.

import numpy as np
n_samples, n_features, n_classes = 200, 10000, 2
rng = np.random.RandomState(42)
X = rng.standard_normal((n_samples, n_features))
y = rng.choice(n_classes, n_samples)

Forma incorrecta

• El uso de todos los datos para la selección de características genera una precisión artificialmente alta, incluso cuando X e y son independientes, lo que debería dar una precisión cercana a 0.5. Esto ocurre porque la selección de características “ve” los datos de prueba, otorgando una ventaja injusta.

• En el enfoque incorrecto, se seleccionan características antes de dividir los datos, lo que infla la precisión del modelo. SelectKBest elige las k mejores características según una función de puntuación (X, y), reteniendo aquellas con mayor relación con y. Si se usa chi2, se evalúa la dependencia entre cada característica e y: valores bajos indican independencia, valores altos sugieren relación no aleatoria. Por defecto, SelectKBest emplea f_regression F-value para medir la relevancia de cada característica.

from sklearn.model_selection import train_test_split
from sklearn.feature_selection import SelectKBest
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.metrics import accuracy_score

• Preprocesamiento incorrecto: se transforman todos los datos

X_selected = SelectKBest(k=25).fit_transform(X, y) #(Dependencia entre cada X[:,i] e y.) -> Reg: F de ANOVA o Class: Chi-cuadrado 

X_train, X_test, y_train, y_test = train_test_split(X_selected, y, random_state=42)
gbc = GradientBoostingClassifier(random_state=1)
gbc.fit(X_train, y_train)

y_pred = gbc.predict(X_test)
accuracy_score(y_test, y_pred)

0.76

Forma correcta

• Para evitar la fuga de datos, primero se deben dividir los datos en entrenamiento y prueba. La selección de características debe realizarse solo con el conjunto de entrenamiento. Al usar fit o fit_transform, se aplica exclusivamente al entrenamiento. Esto garantiza que la puntuación refleje el desempeño real del modelo.

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
select = SelectKBest(k=25)
X_train_selected = select.fit_transform(X_train, y_train)

gbc = GradientBoostingClassifier(random_state=1)
gbc.fit(X_train_selected, y_train)

X_test_selected = select.transform(X_test)
y_pred = gbc.predict(X_test_selected)
accuracy_score(y_test, y_pred)

0.46

• Se recomienda usar un pipeline para encadenar la selección de características y los estimadores, asegurando que solo los datos de entrenamiento se usen en el ajuste y los de prueba solo para evaluar la precisión.

from sklearn.pipeline import make_pipeline

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
pipeline = make_pipeline(SelectKBest(k=25), GradientBoostingClassifier(random_state=1))
pipeline.fit(X_train, y_train)

y_pred = pipeline.predict(X_test)
accuracy_score(y_test, y_pred)

0.46

10.4. Ilustración de la fuga de datos

• Un ejemplo clásico de fuga de información en validación cruzada se encuentra en The Elements of Statistical Learning de Hastie, Tibshirani y Friedman. Reproducimos una versión adaptada: en una tarea de regresión sintética con 100 muestras y 1.000 características, todas se generan de una distribución gaussiana independiente, al igual que la variable respuesta.

import numpy as np

rnd = np.random.RandomState(seed=0)
X = rnd.normal(size=(100, 10000))
y = rnd.normal(size=(100,))

• No hay relación entre los datos \(X\) y el objetivo \(y\) (son independientes), por lo que no debería ser posible aprender nada del conjunto. Se selecciona la característica más informativa con SelectPercentile (elige variables en el percentil más alto de scores) y se evalúa un regresor Ridge mediante validación cruzada.

from sklearn.feature_selection import SelectPercentile, f_regression

select = SelectPercentile(score_func=f_regression, percentile=5).fit(X, y)
X_selected = select.transform(X)
print("X_selected.shape: {}".format(X_selected.shape))

X_selected.shape: (100, 500)

from sklearn.model_selection import cross_val_score
from sklearn.linear_model import Ridge

cross_val_score(Ridge(), X_selected, y, cv=5)

array([0.84834054, 0.94084243, 0.88541709, 0.94012139, 0.91425508])

print("Cross-validation accuracy (cv only on ridge): {:.2f}".format(np.mean(cross_val_score(Ridge(), X_selected, y, cv=5))))

Cross-validation accuracy (cv only on ridge): 0.91

• El score de validación cruzada es 0.91, lo que sugiere un modelo excelente, pero esto es erróneo, ya que los datos son aleatorios. La selección de características eligió, por azar, algunas altamente correlacionadas con el objetivo. Como la selección ocurrió fuera de la validación cruzada, filtró información de los pliegues de prueba, generando resultados poco realistas. Para evitar esto, es necesario aplicar una validación cruzada adecuada con una tubería.

pipe = Pipeline([("select", SelectPercentile(score_func=f_regression, percentile=5)), 
                 ("ridge", Ridge())])

cross_val_score(pipe, X, y, cv=5)

array([-0.97502994, -0.03166358, -0.03989415,  0.03018385, -0.2163673 ])

print("Cross-validation accuracy (pipeline): {:.2f}".format(np.mean(cross_val_score(pipe, X, y, cv=5))))

Cross-validation accuracy (pipeline): -0.25

• La API de scoring siempre maximiza la puntuación. Por ello, las métricas a minimizar (como MSE) se devuelven en negativo, mientras que las que deben maximizarse se mantienen en positivo.

• Pipeline garantiza que la selección de características ocurra dentro de la validación cruzada, evitando la fuga de datos. Esto impide que el modelo seleccione características basadas en información del conjunto de prueba, lo que podría generar resultados engañosos.

10.5. Reduccción de dimensionalidad en el Pipeline

• En tareas de aprendizaje supervisado con datos de alta dimensionalidad, la reducción de dimensionalidad puede ser fundamental para mejorar la eficiencia computacional y evitar el sobreajuste. Una técnica habitual es la aplicación de PCA (Análisis de Componentes Principales) como paso previo al modelado. Para evitar data leakage, estas transformaciones deben integrarse correctamente en un flujo de trabajo reproducible.

• A continuación, se muestra un ejemplo con el conjunto de datos digits donde se implementa un Pipeline que incluye:

  • Estandarización (StandardScaler),

  • Reducción de dimensionalidad (PCA),

  • Clasificación (KNeighborsClassifier),

  junto con una búsqueda de hiperparámetros usando GridSearchCV.

\[ \textsf{StandardScaler}() \Longrightarrow \textsf{PCA}() \Longrightarrow \textsf{KNeighborsClassifier}() \]

from sklearn.decomposition import PCA
from sklearn.neighbors import KNeighborsClassifier
from sklearn.pipeline import Pipeline
from sklearn.model_selection import GridSearchCV
from sklearn.preprocessing import StandardScaler
from sklearn import datasets
import numpy as np
import matplotlib.pyplot as plt

# ==============================
# 1. Datos de ejemplo
# ==============================
X_digits, y_digits = datasets.load_digits(return_X_y=True)

# ==============================
# 2. Definimos el pipeline
# ==============================
pipe = Pipeline(steps=[
    ("scaler", StandardScaler()),
    ("pca", PCA()),
    ("knn", KNeighborsClassifier())
])

# ==============================
# 3. Parámetros para GridSearchCV
# ==============================
param_grid = {
    "pca__n_components": [5, 15, 30, 45, 60],
    "knn__n_neighbors": [3, 5, 7, 9],
    "knn__weights": ["uniform", "distance"]
}

# ==============================
# 4. Búsqueda de hiperparámetros
# ==============================
search = GridSearchCV(pipe, param_grid, n_jobs=-1)
search.fit(X_digits, y_digits)

print(f"Mejor puntuación CV: {search.best_score_:.3f}")
print("Mejores parámetros encontrados:", search.best_params_)

# ==============================
# 5. Extraer PCA y modelo final
# ==============================
best_pca = search.best_estimator_.named_steps["pca"]

# Varianza explicada en proporción
varianza = best_pca.explained_variance_ratio_

# Mostrar las 10 componentes más importantes según PCA
top10 = np.argsort(varianza)[::-1][:10]
print("\nTop 10 componentes PCA por varianza explicada:")
for i in top10:
    print(f"Componente {i+1}: {varianza[i]:.4f}")

# ==============================
# 6. Visualización del espectro PCA
# ==============================
plt.figure(figsize=(6, 4))
plt.plot(np.arange(1, best_pca.n_components_ + 1),
         varianza, marker="+", linewidth=2)
plt.axvline(search.best_estimator_.named_steps["pca"].n_components,
            color='k', linestyle='--', label="n_components elegido")
plt.ylabel("Proporción de varianza explicada")
plt.xlabel("Número de componentes PCA")
plt.legend()
plt.show()

Mejor puntuación CV: 0.948
Mejores parámetros encontrados: {'knn__n_neighbors': 3, 'knn__weights': 'distance', 'pca__n_components': 60}

Top 10 componentes PCA por varianza explicada:
Componente 1: 0.1203
Componente 2: 0.0956
Componente 3: 0.0844
Componente 4: 0.0650
Componente 5: 0.0486
Componente 6: 0.0421
Componente 7: 0.0394
Componente 8: 0.0339
Componente 9: 0.0300
Componente 10: 0.0293

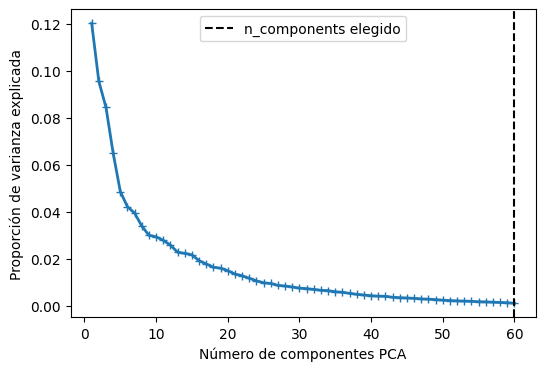
Observación

• Cuando se entrena un pipeline \(\textsf{StandardScaler}() \Longrightarrow \textsf{PCA}() \Longrightarrow \textsf{KNeighborsClassifier}()\) de la siguiente forma:

pipeline.fit(X_train, y_train)

• Ocurre lo siguiente en orden:

1. Paso PCA:

   • El PCA calculó las componentes principales usando X_train.

   • Se quedó con las primeras 60 (por ejemplo) y guardó la matriz de proyección.

2. Paso KNN:

   • Recibió las proyecciones reducidas de X_train (60 columnas en vez de miles).

   • Guardó la posición de cada punto de entrenamiento en ese nuevo espacio.

   • No aprendió “coeficientes”, solo almacenó los puntos (porque KNN es un algoritmo de memoria).

• Cuando llega un nuevo dataset de test

y_pred = pipeline.predict(X_test)

• El pipeline hace automáticamente las mismas transformaciones que usó en entrenamiento, pero sin volver a recalcular nada:

1. Paso PCA:

   • Aplica la misma proyección aprendida con X_train para transformar X_test. Es decir, no vuelve a buscar nuevas componentes, usa las mismas 60 direcciones ya aprendidas.

   • Resta la misma media que usó con X_train. Proyecta X_test sobre las mismas 60 direcciones que aprendió antes.

   • Esto asegura que X_test quede en el mismo espacio de características que X_train.

2. Paso KNN:

   • Calcula la distancia entre cada punto transformado de X_test y todos los puntos de X_train en ese espacio reducido.

   • Busca los k vecinos más cercanos y asigna la clase según weights:

     • "uniform" → todos los vecinos pesan igual.

     • "distance" → vecinos más cercanos pesan más en la votación.

10.6. La interfaz general del Pipeline

• La clase Pipeline no se limita al preprocesamiento y la clasificación, sino que puede combinar múltiples estimadores, como extracción de características, selección, escalado y clasificación, en una secuencia de pasos. También puede incluir regresión o agrupación en lugar de clasificación. El único requisito es que todos los pasos, excepto el último, deben tener un método transform para encadenar su salida con el siguiente paso.

• Durante Pipeline.fit, cada paso aplica fit y transform, excepto el último, que solo usa fit. Internamente, la tubería ejecuta los métodos en secuencia, con pipeline.steps[i][1] representando cada estimador en la lista de pasos.

def fit(self, X, y):
    X_transformed = X
    for name, estimator in self.steps[:-1]:
        # Iterar sobre todo excepto el último paso 
        # Ajustar y transformar los datos
        X_transformed = estimator.fit_transform(X_transformed, y)
    # Ajuste en el último paso
    self.steps[-1][1].fit(X_transformed, y)
    return self

• Cuando se predice utilizando Pipeline, transformamos los datos de forma similar utilizando todos los pasos menos el último paso, y luego llamamos a predict en el último paso

def predict(self, X):
    X_transformed = X
    for step in self.steps[:-1]:
        # Iterar sobre todo excepto el último paso 
        # Ajustar y transformar los datos
        X_transformed = step[1].transform(X_transformed)
    # Ajuste en el último paso
    return self.steps[-1][1].predict(X_transformed)

• El proceso se ilustra en la Fig. 10.1 para dos transformadores, T1, T2, y un classifier (llamado Classifier)

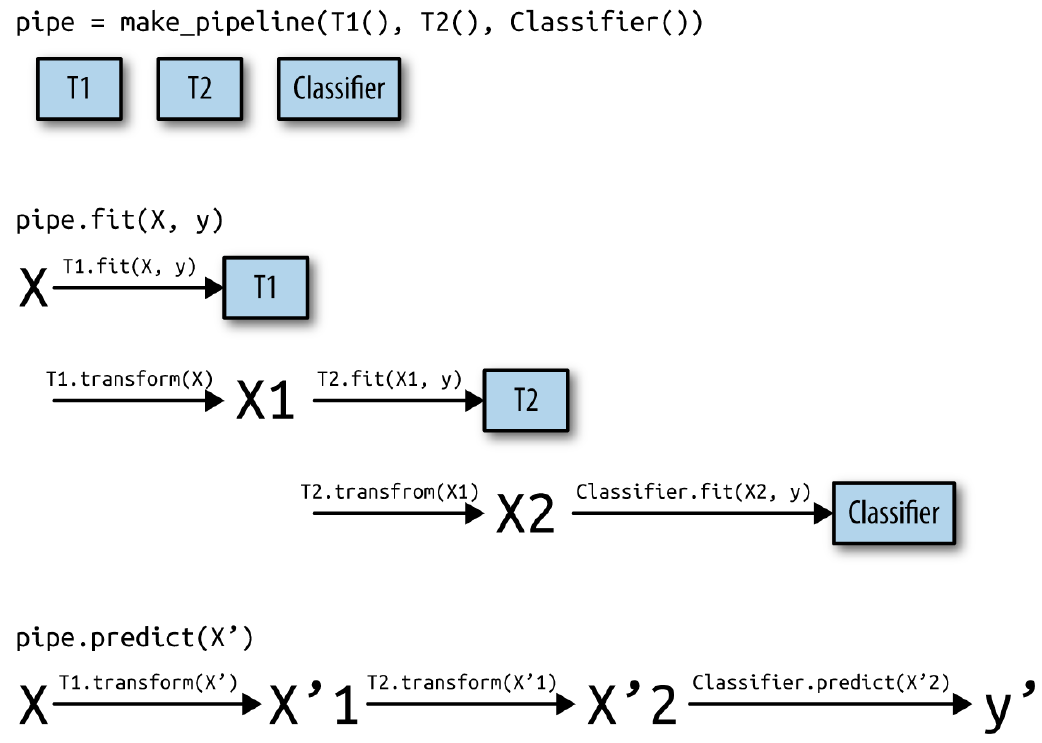
Fig. 10.1 Visión general del proceso de entrenamiento y predicción de la tubería.

• Un Pipeline es más general de lo que parece: no es necesario que el último paso incluya un modelo con función de predicción. Puede componerse solo de transformaciones, como un escalador seguido de un PCA. En ese caso, si el último paso tiene un método transform, el Pipeline también podrá aplicar transform tras procesar los datos en cada etapa previa. Lo único indispensable es que el paso final tenga un método fit.

10.7. Creación cómoda de pipelines con make_pipeline

• La creación de un Pipeline utilizando la sintaxis descrita anteriormente es a veces un poco engorrosa, y a menudo no necesitamos nombres especificados por el usuario para cada paso. Existe una función conveniente make_pipeline, que creará una tubería por nosotros y nombrará automáticamente cada paso basándose en su clase. La sintaxis de make_pipeline es la siguiente

from sklearn.pipeline import make_pipeline

pipe_long = Pipeline([("scaler", MinMaxScaler()), ("svm", SVC(C=100))])
pipe_short = make_pipeline(MinMaxScaler(), SVC(C=100))

• Los objetos pipeline pipe_long y pipe_short hacen exactamente lo mismo, pero pipe_short tiene pasos que fueron nombrados automáticamente. Podemos ver los nombres de los pasos mirando el atributo steps

print("Pipeline steps:\n{}".format(pipe_short.steps))

Pipeline steps:
[('minmaxscaler', MinMaxScaler()), ('svc', SVC(C=100))]

• Los pasos se denominan minmaxscaler y svc. En general, los nombres de los pasos son sólo versiones de los nombres de las clases. Si varios pasos tienen la misma clase, se añade un número

from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA

pipe = make_pipeline(StandardScaler(), PCA(n_components=2), StandardScaler())
print("Pipeline steps:\n{}".format(pipe.steps))

Pipeline steps:
[('standardscaler-1', StandardScaler()), ('pca', PCA(n_components=2)), ('standardscaler-2', StandardScaler())]

• Como puede ver, el primer paso de StandardScaler llamó standardscaler-1 y el segundo standardscaler-2. Sin embargo, en este tipo de configuraciones podría ser mejor utilizar la construcción de tuberías con nombres explícitos, para dar nombres más semánticos a cada paso

10.8. Acceso a los atributos de los pasos

• Para inspeccionar atributos de pasos en un Pipeline, como coeficientes de un modelo o componentes de PCA se utiliza el atributo named_steps, un diccionario que vincula nombres de pasos con sus estimadores. Tras ajustar el pipeline, se pueden extraer, por ejemplo, las dos primeras componentes principales del paso pca aplicado al conjunto de datos cancer.

from sklearn.datasets import load_breast_cancer

cancer = load_breast_cancer()
X = cancer.data
y = cancer.target

pipe.fit(X, y)

components = pipe.named_steps["pca"].components_
print("components.shape: {}".format(components.shape))

components.shape: (2, 30)

10.9. Acceso a los atributos en un Pipeline con GridSearch

• Como hemos comentado anteriormente en este capítulo, una de las principales razones para utilizar pipelines, es para realizar búsquedas en la red. Una tarea común es acceder a algunos de los pasos de una tubería dentro de dentro de una búsqueda en red.

• Busquemos en la red un clasificador LogisticRegression en el conjunto de datos cancer, utilizando Pipeline. Usamos StandardScaler, para escalar los datos antes de pasarlos al clasificador LogisticRegresión. Primero creamos una instancia de nuestro pipeline usando la función make_pipeline.

from sklearn.linear_model import LogisticRegression

pipe = make_pipeline(StandardScaler(), LogisticRegression(max_iter=1000))

• A continuación, creamos un grid de parámetros. Como se explica en la sección anterior, el parámetro de regularización para LogisticRegression es el parámetro C. Utilizamos una red logarítmica para este parámetro, buscando entre 0.01 y 100.

• Como utilizamos la función make_pipeline, el nombre del paso LogisticRegression en el pipeline es el nombre de la clase en minúsculas, logisticregression. Para afinar el parámetro C, tenemos que especificar una red de parámetros para logisticregression__C

param_grid = {'logisticregression__C': [0.01, 0.1, 1, 10, 100]}

• Como es habitual, dividimos el conjunto de datos cancer en conjuntos de entrenamiento y de prueba, y ajustamos una búsqueda en red

X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, random_state=4)
grid = GridSearchCV(pipe, param_grid, cv=5)
grid.fit(X_train, y_train)

GridSearchCV(cv=5,
             estimator=Pipeline(steps=[('standardscaler', StandardScaler()),
                                       ('logisticregression',
                                        LogisticRegression(max_iter=1000))]),
             param_grid={'logisticregression__C': [0.01, 0.1, 1, 10, 100]})

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

• Entonces, ¿cómo accedemos a los coeficientes del mejor modelo LogisticRegression que fue encontrado por GridSearchCV? De los capítulos anteriores sabemos que el mejor modelo encontrado por GridSearchCV, entrenado con todos los datos de entrenamiento, se almacena en grid.best_estimator_

print("Best estimator:\n{}".format(grid.best_estimator_))

Best estimator:
Pipeline(steps=[('standardscaler', StandardScaler()),
                ('logisticregression', LogisticRegression(C=1, max_iter=1000))])

• Este best_estimator_ en nuestro caso es un pipeline con dos pasos, standardcaler y logisticregression. Para acceder al paso de logisticregression, podemos utilizar el atributo named_steps de la tubería, como se ha explicado anteriormente

print("Logistic regression step:\n{}".format(grid.best_estimator_.named_steps["logisticregression"]))

Logistic regression step:
LogisticRegression(C=1, max_iter=1000)

• Ahora que tenemos la instancia de LogisticRegression entrenada, podemos acceder a los coeficientes (pesos) asociados a cada característica de entrada. Para mas información sobre los parámetros que podemos visualizar de este modelo clasificador (ver LogisticRegression). En este caso visualizaremos sus coeficientes usando .coef_. Puede que sea una expresión algo larga, pero a menudo resulta útil para entender los modelos.

print("Logistic regression coefficients:\n{}".format(grid.best_estimator_.named_steps["logisticregression"].coef_))

Logistic regression coefficients:
[[-0.43570655 -0.34266946 -0.40809443 -0.5344574  -0.14971847  0.61034122
  -0.72634347 -0.78538827  0.03886087  0.27497198 -1.29780109  0.04926005
  -0.67336941 -0.93447426 -0.13939555  0.45032641 -0.13009864 -0.10144273
   0.43432027  0.71596578 -1.09068862 -1.09463976 -0.85183755 -1.06406198
  -0.74316099  0.07252425 -0.82323903 -0.65321239 -0.64379499 -0.42026013]]

10.10. Pasos de preprocesamiento GridSearch y Parámetros del Modelo

• Usando pipelines, podemos encapsular todos los pasos de procesamiento en nuestro flujo de trabajo de aprendizaje automático en un único estimador de scikit-learn. Otro beneficio de hacer esto es que ahora podemos ajustar los parámetros de preprocesamiento usando el output de una tarea supervisada, como la regresión o la clasificación. En los capítulos anteriores, utilizamos las funciones polinómicas en el dataset boston antes de aplicar el regresor ridge. Vamos a modelar esto usando un pipeline en su lugar. El proceso contiene tres pasos: escalar los datos, calcular las características polinómicas y la regresión ridge

import pandas as pd

data_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None)
data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
target = raw_df.values[1::2, 2]

X_train, X_test, y_train, y_test = train_test_split(data, target, random_state=0)

from sklearn.preprocessing import PolynomialFeatures

pipe = make_pipeline(StandardScaler(), PolynomialFeatures(), Ridge())

• PolynomialFeatures genera características polinómicas e interacciones hasta un grado especificado. Por ejemplo, para una entrada [a, b] y grado 2, se obtiene [1, a, b, a², ab, b²]. La elección del grado adecuado depende del desempeño del modelo. Se puede optimizar junto con alpha de Ridge usando un param_grid en un pipeline.

param_grid = {'polynomialfeatures__degree': [1, 2, 3], 
              'ridge__alpha': [0.001, 0.01, 0.1, 1, 10, 100]}

• Ahora podemos volver a ejecutar nuestra búsqueda en la red utilizando nuestro param_grid

grid = GridSearchCV(pipe, param_grid=param_grid, cv=5, n_jobs=-1)
grid.fit(X_train, y_train)

GridSearchCV(cv=5,
             estimator=Pipeline(steps=[('standardscaler', StandardScaler()),
                                       ('polynomialfeatures',
                                        PolynomialFeatures()),
                                       ('ridge', Ridge())]),
             n_jobs=-1,
             param_grid={'polynomialfeatures__degree': [1, 2, 3],
                         'ridge__alpha': [0.001, 0.01, 0.1, 1, 10, 100]})

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

• Podemos visualizar el resultado de la validación cruzada utilizando un mapa de calor (ver matshow), como ya se hizo en anteriores secciones

import matplotlib.pyplot as plt

plt.matshow(grid.cv_results_['mean_test_score'].reshape(3, -1), vmin=0, cmap="viridis")
plt.xlabel("ridge__alpha")
plt.ylabel("polynomialfeatures__degree")
plt.xticks(range(len(param_grid['ridge__alpha'])), param_grid['ridge__alpha'])
plt.yticks(range(len(param_grid['polynomialfeatures__degree'])),
param_grid['polynomialfeatures__degree'])
plt.colorbar();

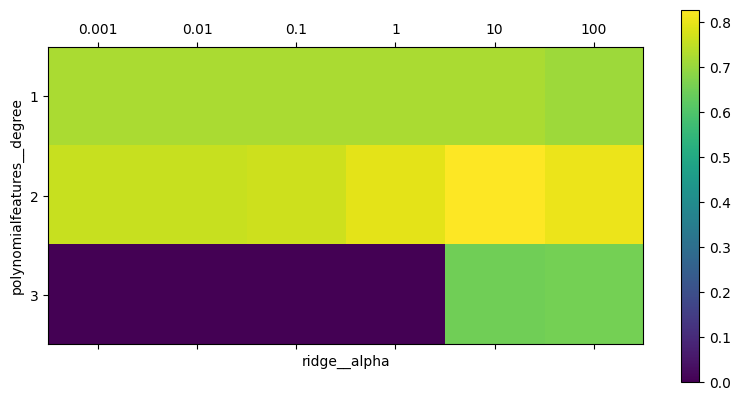
• Observando los resultados producidos por la validación cruzada, podemos ver que el uso de polinomios de grado dos ayuda, pero que los polinomios de grado tres son mucho peores que los de grado uno o dos. Esto se refleja en los mejores parámetros encontrados

print("Best parameters: {}".format(grid.best_params_))

Best parameters: {'polynomialfeatures__degree': 2, 'ridge__alpha': 10}

• Lo que lleva al siguiente score

print("Test-set score: {:.2f}".format(grid.score(X_test, y_test)))

Test-set score: 0.77

• Hagamos una búsqueda en red sin características polinómicas para comparar

param_grid = {'ridge__alpha': [0.001, 0.01, 0.1, 1, 10, 100]}
pipe = make_pipeline(StandardScaler(), Ridge())
grid = GridSearchCV(pipe, param_grid, cv=5)
grid.fit(X_train, y_train)
print("Score without poly features: {:.2f}".format(grid.score(X_test, y_test)))

Score without poly features: 0.63

• El no usar características polinómicas empeora los resultados. Buscar simultáneamente los parámetros del preprocesamiento y del modelo es una estrategia poderosa. Sin embargo, GridSearchCV evalúa todas las combinaciones posibles, por lo que añadir más parámetros incrementa exponencialmente el número de modelos a construir.

10.11. Grid-Searching: ¿Qué modelo usar?

• GridSearchCV puede combinarse con Pipeline para optimizar tanto los hiperparámetros como los pasos de preprocesamiento, como la elección entre StandardScaler o MinMaxScaler, lo cual amplía el espacio de búsqueda y debe aplicarse con cautela.

• Por ejemplo, al comparar SVC y RandomForestClassifier en el conjunto iris, se evalúa si SVC mejora con escalado, mientras que RandomForest no lo requiere. Para ello, se define un Pipeline con dos pasos: preprocesamiento y modelo, utilizando SVC junto con StandardScaler.

pipe = Pipeline([('preprocessing', StandardScaler()), ('classifier', SVC())])

• Definimos parameter_grid para buscar entre RandomForestClassifier y SVC, ajustando sus parámetros y preprocesamiento según el modelo. Usamos una lista de búsqueda para gestionar configuraciones distintas. Para asignar un estimador a un paso, usamos su nombre como parámetro. Si un modelo no requiere preprocesamiento (como RandomForest), configuramos ese paso como None.

from sklearn.ensemble import RandomForestClassifier

param_grid = [{'classifier': [SVC()], 
               'preprocessing': [StandardScaler(), None],
               'classifier__gamma': [0.001, 0.01, 0.1, 1, 10, 100],
               'classifier__C': [0.001, 0.01, 0.1, 1, 10, 100]},
              {'classifier': [RandomForestClassifier(n_estimators=100)],
               'preprocessing': [None], 
               'classifier__max_features': [1, 2, 3]}]

• Ahora podemos instanciar y ejecutar grid search como de costumbre, aquí en el conjunto de datos cancer. Nótes que solo es necesario inicializar pipe con cualquiera de los dos estimadores, luego GridSearchCV se encargará de seleccionar el mejor modelo, basado en el param_grid suministrado.

X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, random_state=0)
grid = GridSearchCV(pipe, param_grid, cv=5)
grid.fit(X_train, y_train)
print("Best params:\n{}\n".format(grid.best_params_))
print("Best cross-validation score: {:.2f}".format(grid.best_score_))
print("Test-set score: {:.2f}".format(grid.score(X_test, y_test)))

Best params:
{'classifier': SVC(C=10, gamma=0.01), 'classifier__C': 10, 'classifier__gamma': 0.01, 'preprocessing': StandardScaler()}

Best cross-validation score: 0.99
Test-set score: 0.98

• El resultado de la búsqueda en la red es que el SVC con el preprocesamiento StandardScaler, C=10 y gamma=0.01 dio el mejor resultado de clasificación, en comparación del el RandomForestClassifier.

Resumen y conclusiones

• La clase Pipeline permite encadenar múltiples pasos de procesamiento en un flujo de trabajo de aprendizaje automático, encapsulándolos en un solo objeto que sigue la interfaz de scikit-learn (fit, predict, transform). Su uso es clave para una evaluación adecuada mediante validación cruzada y búsqueda en red.

• Además, Pipeline simplifica el código y minimiza errores, como olvidar aplicar transformaciones en el conjunto de prueba o desordenar los pasos. La elección de preprocesamiento y modelos requiere ensayo y error, pero Pipeline facilita la experimentación sin excesiva complejidad.

10.12. Proyecto Integrador de Aprendizaje Automático

10.12.1. Contexto del Problema

Las enfermedades cardiovasculares son la principal causa de muerte en todo el mundo, según la OMS. Detectarlas a tiempo es fundamental para evitar complicaciones graves. Con la digitalización de los historiales médicos y la disponibilidad de datos clínicos estructurados, ahora es posible utilizar técnicas de aprendizaje automático para predecir el riesgo de falla cardíaca.

El dataset “Heart Failure Prediction” contiene registros clínicos de pacientes, con variables como presión sanguínea, colesterol, glucosa, edad, entre otras. El objetivo es construir un modelo de clasificación binaria que prediga si un paciente está en riesgo de sufrir una falla cardíaca o no (HeartDisease = 1 o 0).

Este proyecto guía el desarrollo de un flujo completo de Machine Learning Operations (MLOps) de manera local, con herramientas modernas como FastAPI, Docker, Kubernetes, CI/CD con GitHub Actions y monitoreo con Evidently.

10.12.2. Instrucciones para el Desarrollo

1. Descargar el dataset desde Kaggle: Heart Failure Prediction Dataset

2. Crear la estructura de carpetas propuesta en la Etapa 0.

3. Avanza por cada una de las etapas, desde el análisis inicial hasta el monitoreo del modelo en producción.

4. Puedes ejecutar todo localmente (sin necesidad de la nube), usando Docker y Minikube.

5. Cada etapa corresponde a un paso real en el ciclo de vida de un modelo de ML en producción.

10.12.3. Objetivo Final

Desarrollar, evaluar y desplegar un modelo de predicción de falla cardíaca, con control de calidad y monitoreo integrado, aplicando prácticas de MLOps en tu entorno local.

10.12.4. Etapas del Proyecto

Etapa	Descripción
0. Estructura	Crear una estructura modular para alojar código, notebooks, APIs, despliegues y CI/CD.
1. Análisis Exploratorio & Preprocesamiento	Explorar el dataset, tratar valores nulos, evitar data leakage y preparar los datos.
2. Entrenamiento Seguro	Construir un pipeline con GridSearchCV y validación cruzada para evitar errores comunes.
3. Despliegue Local (FastAPI + Docker)	Servir el modelo mediante una API REST. Contenerizar la aplicación con Docker.
4. Orquestación (Kubernetes)	Crear manifiestos de Kubernetes (Deployment y Service) para desplegar el modelo localmente.
5. Integración Continua (GitHub Actions)	Agregar pruebas automáticas, revisión de estilo (linting) y validación del código en cada push.
6. Monitoreo (Evidently)	Generar reportes de deriva de datos (data drift) entre entrenamiento y predicción.

10.12.5. ETAPA 0: Estructura de carpetas

heart-disease-mlops/
├── app/
│   └── api.py
├── docker/
│   ├── Dockerfile
│   └── requirements.txt
├── k8s/
│   ├── deployment.yaml
│   └── service.yaml
├── notebooks/
│   ├── 1_model_leakage_demo.ipynb
│   └── 2_model_pipeline_cv.ipynb
├── .github/
│   └── workflows/
│       └── ci.yml
├── drift_report.html
├── model.joblib
└── README.md

10.12.6. ETAPA 1: Preprocesamiento y detección de Data Leakage

Archivo: notebooks/1_model_leakage_demo.ipynb

Se utiliza el dataset de predicción de enfermedad cardíaca. Puede descargarse desde Kaggle o UCI Machine Learning Repository.

Ejemplo de flujo con y sin data leakage:

import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.svm import SVC
from sklearn.preprocessing import MinMaxScaler
from sklearn.pipeline import Pipeline
from sklearn.metrics import roc_auc_score

# Cargar datos
df = pd.read_csv("heart.csv")

X = df.drop("target", axis=1)
y = df["target"]

# Variable artificial que introduce fuga
np.random.seed(0)
X["leaky_feature"] = y + np.random.normal(0, 0.01, size=len(y))

# Ejemplo con fuga de datos (data leakage)
scaler = MinMaxScaler()
X_scaled = scaler.fit_transform(X)
X_train_l, X_test_l, y_train_l, y_test_l = train_test_split(X_scaled, y, test_size=0.2, random_state=42)

grid_l = GridSearchCV(SVC(probability=True), param_grid={"C": [0.1, 1, 10], "gamma": [0.01, 0.1]}, cv=5, scoring="roc_auc")
grid_l.fit(X_train_l, y_train_l)
auc_l = roc_auc_score(y_test_l, grid_l.predict_proba(X_test_l)[:, 1])

# Flujo correcto (sin fuga)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

pipe = Pipeline([("scaler", MinMaxScaler()), ("svc", SVC(probability=True))])
param_grid = {"svc__C": [0.1, 1, 10], "svc__gamma": [0.01, 0.1]}
grid = GridSearchCV(pipe, param_grid, cv=5, scoring="roc_auc")
grid.fit(X_train, y_train)
auc = roc_auc_score(y_test, grid.predict_proba(X_test)[:, 1])

print(f"AUC con fuga: {auc_l:.3f}")
print(f"AUC sin fuga: {auc:.3f}")

1. Implementar todos los modelos vistos hasta esta sección. Sugerencia: Agrega al menos tres clasificadores adicionales al flujo sin fuga (RandomForest, KNN, LogisticRegression, etc.) utilizando Pipeline y GridSearchCV, y compara sus resultados (AUC) con los obtenidos por SVC.

Modelos recomendados:

• LogisticRegression

• RandomForestClassifier

• KNeighborsClassifier

• GradientBoostingClassifier

Requisitos:

• Implementar cada modelo dentro de un Pipeline

• Utilizar GridSearchCV para optimizar hiperparámetros

• Comparar AUC y Accuracy

• Presentar un ranking comparativo

2. Separar código en funciones reutilizables. Sugerencia: Encapsula la lógica de entrenamiento y evaluación en funciones claras y reutilizables.

Ejemplo:

def train_pipeline(X_train, y_train, model, param_grid):
    pipe = Pipeline([("scaler", MinMaxScaler()), ("clf", model)])
    grid = GridSearchCV(pipe, param_grid, cv=5, scoring="roc_auc")
    grid.fit(X_train, y_train)
    return grid

10.12.7. ETAPA 2: Modelado con validación segura

Archivo: notebooks/2_model_pipeline_cv.ipynb

Este cuaderno debe contener:

• División de los datos antes del escalado

• Implementación de Pipeline con GridSearchCV

• Evaluación del modelo con matriz de confusión, curva ROC y AUC

10.12.8. ETAPA 3: Despliegue con FastAPI y Docker

Archivo: app/api.py

API para predicciones en tiempo real:

from fastapi import FastAPI
from pydantic import BaseModel
import joblib
import numpy as np

model = joblib.load("app/model.joblib")
app = FastAPI()

class Input(BaseModel):
    features: list

@app.post("/predict")
def predict(data: Input):
    X = np.array(data.features).reshape(1, -1)
    proba = model.predict_proba(X)[0][1]
    return {"heart_disease_probability": proba, "prediction": int(proba > 0.5)}

Exportación del modelo:

import joblib
joblib.dump(grid.best_estimator_, "app/model.joblib")

Archivo: docker/Dockerfile

FROM python:3.10-slim
WORKDIR /app
COPY docker/requirements.txt .
RUN pip install --no-cache-dir -r requirements.txt
COPY app/ ./app/
CMD ["uvicorn", "app.api:app", "--host", "0.0.0.0", "--port", "8000"]

Archivo: docker/requirements.txt

fastapi
uvicorn
scikit-learn
joblib
pydantic

Construcción y ejecución local:

docker build -t heart-api -f docker/Dockerfile .
docker run -p 8000:8000 heart-api

10.12.9. ETAPA 4: Despliegue en Kubernetes local

Archivo: k8s/deployment.yaml

apiVersion: apps/v1
kind: Deployment
metadata:
  name: heart-model
spec:
  replicas: 1
  selector:
    matchLabels:
      app: heart-model
  template:
    metadata:
      labels:
        app: heart-model
    spec:
      containers:
      - name: model
        image: <TU_USUARIO_DOCKER>/heart-api
        ports:
        - containerPort: 8000

Archivo: k8s/service.yaml

apiVersion: v1
kind: Service
metadata:
  name: heart-service
spec:
  selector:
    app: heart-model
  ports:
    - protocol: TCP
      port: 80
      targetPort: 8000
  type: LoadBalancer

Comandos para desplegar:

kubectl apply -f k8s/deployment.yaml
kubectl apply -f k8s/service.yaml
kubectl get svc

10.12.10. ETAPA 5: Integración continua con GitHub Actions

Archivo: .github/workflows/ci.yml

name: CI
on: [push]
jobs:
  build:
    runs-on: ubuntu-latest
    steps:
      - uses: actions/checkout@v3
      - name: Set up Python
        uses: actions/setup-python@v4
        with:
          python-version: '3.10'
      - name: Install dependencies
        run: |
          pip install -r docker/requirements.txt
          pip install flake8 pytest
      - name: Lint
        run: flake8 app/
      - name: Tests
        run: pytest tests/

10.12.11. ETAPA 6: Monitoreo de deriva de datos

Uso de Evidently para monitoreo:

from evidently.report import Report
from evidently.metric_preset import DataDriftPreset

report = Report(metrics=[DataDriftPreset()])
report.run(reference_data=X_train, current_data=X_test)
report.save_html("drift_report.html")

10.12.12. README.md

# Data Lake + Forecasting + Dashboard (MLOps local con Docker)

Este proyecto es una arquitectura local basada en herramientas open source y Docker para construir un **Data Lake local**, realizar **modelos de forecasting** y desplegar un **dashboard interactivo**. Está orientado a escenarios comerciales como análisis SELL IN / SELL OUT y toma de decisiones predictivas.

## Arquitectura y tecnologías utilizadas

- **MinIO**: almacenamiento de datos tipo S3 (Data Lake local)
- **Apache Spark**: procesamiento de datos y modelos de ML
- **Prophet (Facebook)**: modelos de forecasting de series temporales
- **Streamlit**: visualización interactiva
- **Airflow**: orquestación de pipelines
- **Docker**: contenedores para todas las herramientas
- **Jupyter Notebooks**: desarrollo y pruebas de los pasos