Errores comunes y Tratamiento de Datos Faltantes y Atípicos#
Objetivos
Identificar los errores que se cometen al crear visualizaciones
Aplicar técnicas para corregir los errores y crear visualizaciones eficaces
Seleccionar y diseñar las visualizaciones adecuadas para determinados tipos de datos
Describir las diferentes bibliotecas y herramientas disponibles para producir visualizaciones
Introducción#
En éste capítulo se enumera y explica los posibles fallos y errores que se cometen durante varias etapas del proceso de visualización de datos, como la visualización de elementos no correlacionados de un conjunto de datos para mostrar una relación o crear una característica interactiva inapropiada.
El proceso de visualización de datos puede parecer sencillo: tome algunos datos, trace algunos gráficos, añadir algunas características interactivas, y el trabajo está hecho. O, tal vez, no lo sea: podría haber varios lugares durante el trayecto en los que se pueden cometer errores. Estos errores terminan por dar lugar a una visualización defectuosa que no puede de manera fácil y eficaz transmitir lo que dicen los datos, lo que hace que sea completamente inútil para el público que lo está viendo.
Formato e interpretación de datos#
La primera fase de la visualización de datos es entender los datos frente a ti: entender lo que es, lo que significa y lo que transmite. Solo cuando entiendas los datos serás capaz de diseñar una visualización que ayude a otros a entenderlos.
Además, es importante asegurarse de que los datos tienen sentido y contienen suficiente información, ya sea categórica, numérica o una mezcla de ambas, para ser visualizados. Por lo tanto, si tratas con datos erróneos o sucios, es probable que la visualización sea defectuosa.
En esta siguiente sección, veremos algunas formas de evitar los errores comunes que se suelen cometidos en esta fase de los datos y cómo evitarlos.
¿Cómo evitar los errores más comunes al tratar con datos sucios?
Garbage In, Garbage Out: Este es un dicho popular en el campo de la ciencia de datos, especialmente con respecto a la visualización de datos. Básicamente, significa que si utilizas datos desordenados y ruidosos, vas a obtener una visualización defectuosa y poco informativa. Los datos desordenados, ruidosos y sucios corresponden a una serie de problemas que se encuentran en los datos. Vamos a discutir los problemas uno por uno y las formas de tratar este tipo de datos.
Valores atípicos
Los datos que contienen valores inexactos o instancias que son significativamente diferentes del resto de los datos de un dataset se denominan valores atípicos. Estos valores atípicos pueden ser auténticos, es decir, parecen incorrectos, pero en realidad no lo son, o son errores que se cometen al recoger o almacenar los datos.
Veamos un ejemplo de un error cometido al recoger o almacenar los datos. La siguiente tabla muestra la edad, el peso y el sexo de los clientes que acuden a un determinado gimnasio. La columna de sexo consta de tres valores discretos 0, 1 y 2 que corresponden todos a una clase: hombre, mujer y otro, respectivamente. La columna de la edad se expresa en años y la columna de peso está en kilogramos
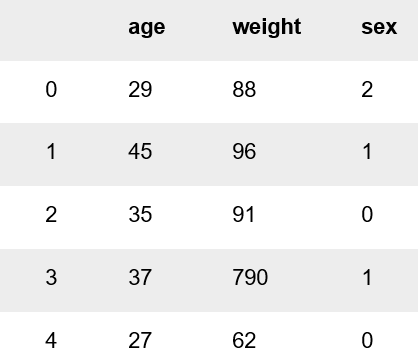
Todo parece correcto hasta que llegamos a la cuarta instancia (índice 3), donde el peso es de 790 kg. Esto parece extraño porque nadie puede pesar realmente 790 kg, especialmente alguien cuya estatura es de 1,5 metros y 7 pulgadas. Quien haya almacenado estos datos debe haber querido decir 79 kg y haber añadido un 0 por error.
Este es un caso de un valor atípico en el conjunto de datos. Esto puede parecer trivial en este momento, sin embargo, esto puede resultar en visualizaciones y predicciones o patrones de modelos de aprendizaje automático defectuosos, especialmente si hay múltiples repeticiones de esos datos. Ahora, veamos un ejemplo de un auténtico valor atípico en la siguiente tabla.
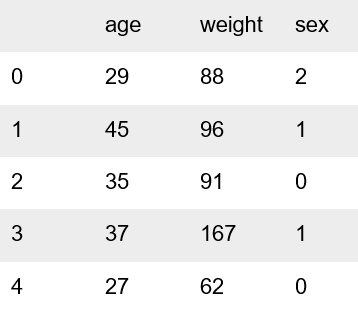
El peso en el cuarto caso (índice 3) es de 167 kilogramos, lo que parece extrañamente alto. Sin embargo, sigue siendo un valor verosímil, ya que es posible que alguien tenga un peso de 167 kilogramos a los 37 años. Por lo tanto, se trata de un verdadero valor atípico. Mientras que en los ejemplos anteriores es fácil detectar el valor atípico, ya que solo hay 5 casos, en realidad, nuestros conjuntos de datos son masivos, por lo que comprobar cada caso es una tarea tediosa y poco práctica.
En consecuencia, en la vida real, podemos utilizar visualizaciones estáticas básicas, como los gráficos de caja, para observar la existencia de valores atípicos. Los gráficos de caja son visualizaciones de datos sencillas, pero informativas que pueden decirnos mucho sobre la forma en que se distribuyen nuestros datos. Muestran el rango de nuestros datos basándose en cinco valores clave:
El valor mínimo de la columna
El primer cuartil
La mediana
El tercer cuartil
El valor máximo de la columna
Esto es lo que hace que sean excelentes para mostrar los valores atípicos, además de describir la simetría de los datos, el grado de agrupación de los mismos (si todos los valores están repartidos en un amplio rango), y si están o no sesgados.
Visualización de valores atípicos en un conjunto de datos con un gráfico de cajas#
En este ejercicio, vamos a crear un gráfico de caja para comprobar si nuestro conjunto de datos contiene valores atípicos. Vamos a utilizar el conjunto de datos gym.csv, que contiene información sobre los clientes de un determinado gimnasio.
Importar las librerías necesarias
import warnings
warnings.filterwarnings('ignore')
import pandas as pd
import numpy as np
import plotly.express as px
Guarda el archivo gym.csv en un DataFrame llamado gym, e imprime las cinco primeras filas del mismo para ver cómo son los datos
gym = pd.read_csv('https://raw.githubusercontent.com/lihkir/Uninorte/main/AppliedStatisticMS/DataVisualizationRPython/Lectures/Python/PythonDataSets/gym.csv')
gym.head()
| age | weight | sex | |
|---|---|---|---|
| 0 | 29 | 88 | 2 |
| 1 | 45 | 96 | 1 |
| 2 | 35 | 91 | 0 |
| 3 | 37 | 790 | 1 |
| 4 | 27 | 62 | 0 |
Como puede ver, nuestros datos tienen tres columnas:
age, weight, sex. La columna sexo consta de tres valores discretos que corresponden a tres clases discretas:0 es hombre,1 es mujery2 es otro.Cree un gráfico de caja con el eje \(x\) como columna de sexo y el eje \(y\) como peso
fig = px.box(gym, x = 'sex', y = 'weight', notched = False)
fig.show()
La escala del eje \(y\) es extrañamente grande, ya que todos los gráficos de caja están comprimidos en la octava parte inferior del gráfico, por lo que no representa una visualización clara de los datos. Esto se debe al valor atípico en la cuarta instancia de nuestro
DataFrame790 kgTodos los valores parecen estar bien, excepto ese valor atípico en la parte superior del gráfico con max=790. Ahora, veremos las formas de tratar los valores atípicos.
Cómo tratar los valores atípicos
Hay tres formas principales de tratar los valores atípicos:
Eliminación: Si sólo hay unas pocas instancias (filas) que poseen valores atípicos, entonces esas instancias pueden ser eliminadas completamente del conjunto de datos, dejando así un conjunto de datos con cero valores atípicos. También hay ocasiones en las que una determinada característica (columna) contiene un gran número de valores atípicos. En tal caso, esa característica concreta puede eliminarse del conjunto de datos pero sólo si esa característica es insignificante. Sin embargo, la eliminación de datos no siempre es la mejor idea.
Imputación: La imputación es una opción mejor que la eliminación, especialmente si hay muchos valores atípicos en el conjunto de datos. Esto puede hacerse de tres maneras:
La forma más común es imputar los valores atípicos con la media, la mediana o la moda de la columna. Sin embargo, en el caso de muchos valores atípicos, estos valores pueden no ser lo suficientemente bueno, ya que cada valor atípico será un problema, debido a que cada uno de estos valores será sustituido por el mismo valor (la media, la mediana o la moda)
El otro método para obtener mejores valores para los valores atípicos, especialmente en el caso de series temporales, es la interpolación lineal, es decir, el uso de polinomios lineales para crear nuevos puntos de datos dentro de un rango definido de puntos conocidos para reemplazar valores atípicos.
Un modelo de regresión lineal también puede utilizarse para predecir un valor que falta si es numérico, y en el caso de que el valor que falta sea categórico, se puede utilizar un modelo de regresión logística.
Por ejemplo, supongamos que tiene un conjunto de datos del que necesita mostrar una relación entre la altura y el peso. La columna de la altura tiene varios valores perdidos, pero, como es una característica significativa, no puede eliminarla, ni tampoco puede imputar la media de la columna, ya que eso podría llevar a una relación falsa. El conjunto de datos puede dividirse en dos conjuntos de datos
El conjunto de datos de entrenamiento, que contiene instancias sin valores perdidos
El nuevo conjunto de datos, que contiene solo los casos en los que faltan valores en la columna de altura.
A continuación, se puede utilizar un modelo de regresión lineal en el conjunto de datos de entrenamiento. El modelo aprenderá de estos datos y, cuando se le proporcione el nuevo conjunto de datos, podrá predecir los valores de la columna de altura. Ahora, los dos conjuntos de datos pueden fusionarse juntos y ser utilizados para crear visualizaciones, ya que no hay valores perdidos.
Cómo tratar los valores atípicos#
Detección de valores atípicos
Si nuestro conjunto de datos es pequeño, podemos detectar el valor atípico simplemente mirando el conjunto de datos. Pero si tenemos un conjunto de datos enorme, ¿cómo podemos identificar los valores atípicos? Tenemos que utilizar técnicas de visualización y matemáticas. A continuación se presentan algunas de las técnicas de detección de valores atípicos
Boxplots
Puntuación \(Z\)
Rango intercuantil (IQR)
Detección de valores atípicos mediante las puntuaciones \(Z\)
Criterio: Cualquier dato cuya puntuación \(Z\) esté fuera de la tercera desviación estándar es un valor atípico

Implementación:
Recorrer todos los datos y calcular la puntuación \(Z\) mediante la fórmula \((X_{i}-\mu)/\sigma\). Definir un valor de umbral de 3 y marcar los puntos de datos cuyo valor absoluto de puntuación \(Z\) sea mayor que el umbral como valores atípicos. Recuerde que por el Teorema de Chebyshev un 99.7% de los datos están contenidos en el intervalo \(\mu\pm 3\sigma\).
import numpy as np
outliers = []
def detect_outliers_zscore(data):
thres = 3
mean = np.mean(data)
std = np.std(data)
for i in data:
z_score = (i - mean)/std
if (np.abs(z_score) > thres):
outliers.append(i)
return outliers
sample_outliers = detect_outliers_zscore(gym.weight)
print("Outliers from Z-scores method: ", sample_outliers)
Outliers from Z-scores method: [790]
Detección de valores atípicos mediante el rango intercuantil (IQR)
Criterio: Los datos que se sitúan 1.5 veces del IQR por encima de \(Q_{3}\) y por debajo de \(Q_{1}\) son valores atípicos.
Implementación
Ordenar el conjunto de datos de forma ascendente
Calcular los cuartiles 1 y 3 \((Q_{1}, Q_{3})\)
Calcular \(IQR=Q_{3}-Q_{1}\)
Calcular el límite inferior = \((Q_{1}-1.5*IQR)\), el límite superior = \((Q_{3}+1.5*IQR)\), recorrer los valores del conjunto de datos y comprobar los que están por debajo del límite inferior y por encima del límite superior y marcarlos como valores atípicos
outliers = []
def detect_outliers_iqr(data):
data = sorted(data)
q1 = np.percentile(data, 25)
q3 = np.percentile(data, 75)
IQR = q3-q1
lwr_bound = q1-(1.5*IQR)
upr_bound = q3+(1.5*IQR)
for i in data:
if (i<lwr_bound or i>upr_bound):
outliers.append(i)
return outliers
sample_outliers = detect_outliers_iqr(gym.weight)
print("Outliers from IQR method: ", sample_outliers)
Outliers from IQR method: [790]
Tratamiento de los valores atípicos#
Eliminación
En este ejercicio, vamos a eliminar la instancia que contiene el valor atípico del conjunto de datos que utilizamos en el ejercicio previo, y visualizamos el conjunto de datos de nuevo generando un gráfico de caja basado en el nuevo conjunto de datos.
Importar las librerías necesarias
import pandas as pd
import numpy as np
import plotly.express as px
Guarda el archivo gym.csv en un DataFrame llamado gym, e imprime las cinco primeras filas del mismo para ver cómo son los datos
gym = pd.read_csv('https://raw.githubusercontent.com/lihkir/Uninorte/main/AppliedStatisticMS/DataVisualizationRPython/Lectures/Python/PythonDataSets/gym.csv')
gym.head()
| age | weight | sex | |
|---|---|---|---|
| 0 | 29 | 88 | 2 |
| 1 | 45 | 96 | 1 |
| 2 | 35 | 91 | 0 |
| 3 | 37 | 790 | 1 |
| 4 | 27 | 62 | 0 |
Modificar el DataFrame del gimnasio para que solo esté formado por los casos en los que el peso sea inferior a 104 e imprimir las cinco primeras filas:
gym_del = gym[gym.weight < 104]
gym_del.head()
| age | weight | sex | |
|---|---|---|---|
| 0 | 29 | 88 | 2 |
| 1 | 45 | 96 | 1 |
| 2 | 35 | 91 | 0 |
| 4 | 27 | 62 | 0 |
| 5 | 58 | 55 | 0 |
Vamos a crear un boxplot para ver el aspecto de los datos
fig1 = px.box(gym_del, x = 'sex', y = 'weight', notched = True)
fig1
Imputación por medio de la media, mediana o moda
Como el valor medio es sensible a valores atípicos, se aconseja sustituirlos por la mediana
median = np.median(gym.weight)
print("median: ", median)
for outlier in sample_outliers:
gym.weight = np.where(gym.weight == outlier, median, gym.weight)
median: 76.0
gym.head()
| age | weight | sex | |
|---|---|---|---|
| 0 | 29 | 88.0 | 2 |
| 1 | 45 | 96.0 | 1 |
| 2 | 35 | 91.0 | 0 |
| 3 | 37 | 76.0 | 1 |
| 4 | 27 | 62.0 | 0 |
fig1 = px.box(gym, x = 'sex', y = 'weight', notched = True)
fig1
Tratamiento de los valores faltantes#
Datos faltantes
Los datos perdidos son, como su nombre indica, valores que están en blanco (NaN, -, 0 cuando no deberían ser 0, etc.). Al igual que los valores atípicos, los valores perdidos pueden ser problemáticos tanto en el caso de las visualizaciones como en el de los modelos predictivos.
Los valores faltantes en las visualizaciones pueden mostrar una tendencia que en realidad no existe o no representa una relación entre dos variables que, en realidad, es significativa. Aunque es posible crear visualizaciones con un conjunto de datos que contenga valores perdidos, no se recomienda hacerlo. Al hacerlo, se ignoran los casos en los que se encuentran esos valores perdidos, creando así una visualización basada en algunos de los datos pero no en todos.
Por lo tanto, el tratamiento de los valores perdidos es de suma importancia. Existen dos enfoques principales para tratar los valores perdidos: la supresión y la imputación, ambos discutidos en términos de tratamiento de los valores atípicos. La misma lógica se aplica a los valores faltantes.
En este ejercicio, vamos a trabajar con un conjunto de datos que tiene siete valores perdidos en forma de 0s. En primer lugar, eliminaremos las instancias que contienen estos valores perdidos y se genera un gráfico de caja para ver el impacto que la eliminación de un gran número de instancias en nuestra visualización. A continuación, imputaremos el valor de la mediana de la columna que contiene los valores perdidos y generaremos un gráfico de caja basado en este conjunto de datos imputados.
Importar las librerías necesarias
import pandas as pd
import numpy as np
import plotly.express as px
Guarda el archivo weight.csv en un
DataFramellamado weight, e imprime las cinco primeras filas del mismo para ver cómo son los datos y utiliza la función.describe()para mostrar información sobre ella
w = pd.read_csv('https://raw.githubusercontent.com/lihkir/Uninorte/main/AppliedStatisticMS/DataVisualizationRPython/Lectures/Python/PythonDataSets/weight.csv')
w.head()
| weight | sex | |
|---|---|---|
| 0 | 47 | 2 |
| 1 | 0 | 1 |
| 2 | 35 | 0 |
| 3 | 34 | 1 |
| 4 | 0 | 0 |
w.describe()
| weight | sex | |
|---|---|---|
| count | 62.000000 | 62.000000 |
| mean | 33.887097 | 0.838710 |
| std | 15.683451 | 0.813685 |
| min | 0.000000 | 0.000000 |
| 25% | 25.000000 | 0.000000 |
| 50% | 35.000000 | 1.000000 |
| 75% | 46.000000 | 1.750000 |
| max | 56.000000 | 2.000000 |
Como podemos ver, el valor de peso mínimo en nuestro conjunto de datos es 0; sin embargo, nadie puede pesar 0 kgs, lo que significa que tenemos valores faltantes en forma de 0s. Intentemos eliminar estas instancias.
Cree un nuevo
DataFrameque conste sólo de las instancias en las que el peso no sea igual a 0. Muestre información sobre este nuevoDataFrame
doc_w = w[w.weight != 0]
doc_w.describe()
| weight | sex | |
|---|---|---|
| count | 55.00000 | 55.000000 |
| mean | 38.20000 | 0.836364 |
| std | 10.49056 | 0.811118 |
| min | 21.00000 | 0.000000 |
| 25% | 31.00000 | 0.000000 |
| 50% | 36.00000 | 1.000000 |
| 75% | 46.50000 | 1.500000 |
| max | 56.00000 | 2.000000 |
Crea un
boxplotcon este nuevoDataFrame, con el eje \(x\) como sexo y el eje \(y\) como peso
fig1 = px.box(doc_w, x = 'sex', y = 'weight', notched = True)
fig1
Ahora, el valor del peso mínimo es 21, lo que tiene más sentido. Sin embargo, nuestro conteo se ha reducido a 55 de 62, lo que significa que se han eliminado 7 instancias de nuestro conjunto de datos. Esto puede parecer pequeño en este ejemplo, pero en realidad, esto puede tener repercusiones serias en la información obtenida.
Además, en el gráfico de caja anterior, el extremo inferior de la caja para el sexo 0 y el extremo superior de la caja para el sexo 2 es ligeramente anormal. Por lo tanto, sustituyamos los valores 0 de la columna de peso por el valor medio de la columna. Recuerde que tenemos que calcular la media de la columna ¡columna sin tener en cuenta esos valores 0! Si los tenemos en cuenta, entonces nuestra media será incorrecta.
Calcular la mediana de la columna de pesos del
DataFrameque consiste en sólo valores de peso distintos de cero
median_w = doc_w['weight'].median()
median_w
36.0
Utilice la función
.replace()para sustituir los valores 0 presentes en la columna weight delDataFrameoriginal por la mediana de la columna weight del modificado. Guarde esto en un nuevoDataFrame
w_new = w.replace({'weight': {0: median_w}})
Muestra la información del nuevo
DataFrame
w_new.describe()
| weight | sex | |
|---|---|---|
| count | 62.000000 | 62.000000 |
| mean | 37.951613 | 0.838710 |
| std | 9.895234 | 0.813685 |
| min | 21.000000 | 0.000000 |
| 25% | 31.250000 | 0.000000 |
| 50% | 36.000000 | 1.000000 |
| 75% | 46.000000 | 1.750000 |
| max | 56.000000 | 2.000000 |
Nuestro recuento es de 62, lo que significa que tenemos todas las instancias, y nuestro peso mínimo es 21, lo que significa que no tenemos ningún 0.
Cree un gráfico de caja con este nuevo
DataFrame, con el eje \(x\) como sex y el eje \(y\) como weight.
fig2 = px.box(w_new, x = 'sex', y = 'weight', notched = True)
fig2
Imputación múltiple iterativa#
Ahora, tenemos una visualización que no tiene valores perdidos y representa todas las instancias que están presentes en el conjunto de datos. Veamos el tercer problema que puede generar una visualización defectuosa. Otras técnicas de imputación de datos fueron estudiadas en R, y se pueden importar a Python. En Python,
MICEse puede ejecutar en un paquete llamado IterativeImputer, el cual está en fase experimental y está disponible en el paquetesklearn.impute.La siguiente figura describe como funciona la imputación múltiple iterativa, la cual seguiremos analizando también usando el lenguaje
R
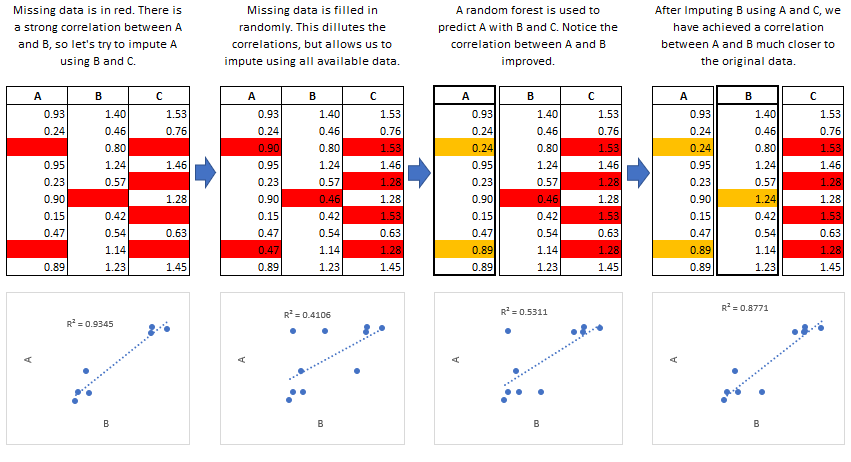
Fig. 1 Funcionamiento del método de imputación múltiple por ecuaciones encadenadas.#

Fig. 2 Funcionamiento del método de imputación por emparejamiento predictivo medio.#
Aplicación de IterativeImputer#
El conjunto de datos del presente ejemplo, describe las características médicas de caballos con cólico y si sobrevivieron o murieron (ver horse-colic). Hay 300 filas y 26 variables de entrada con una variable de salida. Es una tarea de predicción de clasificación binaria que implica predecir 1 si el caballo vivió y 2 si el caballo murió.
Hay muchos campos que podríamos seleccionar para predecir en este conjunto de datos. En este caso, predeciremos si el problema fue quirúrgico o no (índice de columna 23), convirtiéndolo en un problema de clasificación binaria.
23: outcomewhat eventually happened to the horse?
possible values:
1 =
lived2 =
died3 =
was euthanized
El conjunto de datos tiene muchos valores faltantes para muchas de las columnas, donde cada valor faltante está marcado con un carácter de interrogación (“?”).
Podemos cargar el conjunto de datos usando la función
read_csv()y especificar losna_valuespara cargar los valores de'?'como datos faltantes, marcados con un valorNaN
dataframe = pd.read_csv("https://raw.githubusercontent.com/lihkir/Data/main/horse-colic.csv", header=None, na_values='?')
dataframe.head()
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ... | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2.0 | 1 | 530101 | 38.5 | 66.0 | 28.0 | 3.0 | 3.0 | NaN | 2.0 | ... | 45.0 | 8.4 | NaN | NaN | 2.0 | 2 | 11300 | 0 | 0 | 2 |
| 1 | 1.0 | 1 | 534817 | 39.2 | 88.0 | 20.0 | NaN | NaN | 4.0 | 1.0 | ... | 50.0 | 85.0 | 2.0 | 2.0 | 3.0 | 2 | 2208 | 0 | 0 | 2 |
| 2 | 2.0 | 1 | 530334 | 38.3 | 40.0 | 24.0 | 1.0 | 1.0 | 3.0 | 1.0 | ... | 33.0 | 6.7 | NaN | NaN | 1.0 | 2 | 0 | 0 | 0 | 1 |
| 3 | 1.0 | 9 | 5290409 | 39.1 | 164.0 | 84.0 | 4.0 | 1.0 | 6.0 | 2.0 | ... | 48.0 | 7.2 | 3.0 | 5.3 | 2.0 | 1 | 2208 | 0 | 0 | 1 |
| 4 | 2.0 | 1 | 530255 | 37.3 | 104.0 | 35.0 | NaN | NaN | 6.0 | 2.0 | ... | 74.0 | 7.4 | NaN | NaN | 2.0 | 2 | 4300 | 0 | 0 | 2 |
5 rows × 28 columns
dataframe.describe()
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ... | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 299.000000 | 300.000000 | 3.000000e+02 | 240.000000 | 276.000000 | 242.000000 | 244.000000 | 231.000000 | 253.000000 | 268.000000 | ... | 271.000000 | 267.000000 | 135.000000 | 102.000000 | 299.000000 | 300.000000 | 300.000000 | 300.000000 | 300.000000 | 300.000000 |
| mean | 1.397993 | 1.640000 | 1.085889e+06 | 38.167917 | 71.913043 | 30.417355 | 2.348361 | 2.017316 | 2.853755 | 1.305970 | ... | 46.295203 | 24.456929 | 2.037037 | 3.019608 | 1.551839 | 1.363333 | 3657.880000 | 90.226667 | 7.363333 | 1.670000 |
| std | 0.490305 | 2.173972 | 1.529801e+06 | 0.732289 | 28.630557 | 17.642231 | 1.045054 | 1.042428 | 1.620294 | 0.477629 | ... | 10.419335 | 27.475009 | 0.804905 | 1.968567 | 0.737187 | 0.481763 | 5399.513513 | 649.569234 | 127.536674 | 0.470998 |
| min | 1.000000 | 1.000000 | 5.184760e+05 | 35.400000 | 30.000000 | 8.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | ... | 23.000000 | 3.300000 | 1.000000 | 0.100000 | 1.000000 | 1.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 |
| 25% | 1.000000 | 1.000000 | 5.289040e+05 | 37.800000 | 48.000000 | 18.500000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | ... | 38.000000 | 6.500000 | 1.000000 | 2.000000 | 1.000000 | 1.000000 | 2111.750000 | 0.000000 | 0.000000 | 1.000000 |
| 50% | 1.000000 | 1.000000 | 5.303055e+05 | 38.200000 | 64.000000 | 24.500000 | 3.000000 | 2.000000 | 3.000000 | 1.000000 | ... | 45.000000 | 7.500000 | 2.000000 | 2.250000 | 1.000000 | 1.000000 | 2673.500000 | 0.000000 | 0.000000 | 2.000000 |
| 75% | 2.000000 | 1.000000 | 5.347275e+05 | 38.500000 | 88.000000 | 36.000000 | 3.000000 | 3.000000 | 4.000000 | 2.000000 | ... | 52.000000 | 57.000000 | 3.000000 | 3.900000 | 2.000000 | 2.000000 | 3209.000000 | 0.000000 | 0.000000 | 2.000000 |
| max | 2.000000 | 9.000000 | 5.305629e+06 | 40.800000 | 184.000000 | 96.000000 | 4.000000 | 4.000000 | 6.000000 | 3.000000 | ... | 75.000000 | 89.000000 | 3.000000 | 10.100000 | 3.000000 | 2.000000 | 41110.000000 | 7111.000000 | 2209.000000 | 2.000000 |
8 rows × 28 columns
Luego podemos enumerar cada columna y reportar el número de filas con valores faltantes para esa columna.
for i in range(dataframe.shape[1]):
n_miss = dataframe[[i]].isnull().sum()
perc = n_miss / dataframe.shape[0] * 100
print('> %d, Missing: %d (%.1f%%)' % (i, n_miss, perc))
> 0, Missing: 1 (0.3%)
> 1, Missing: 0 (0.0%)
> 2, Missing: 0 (0.0%)
> 3, Missing: 60 (20.0%)
> 4, Missing: 24 (8.0%)
> 5, Missing: 58 (19.3%)
> 6, Missing: 56 (18.7%)
> 7, Missing: 69 (23.0%)
> 8, Missing: 47 (15.7%)
> 9, Missing: 32 (10.7%)
> 10, Missing: 55 (18.3%)
> 11, Missing: 44 (14.7%)
> 12, Missing: 56 (18.7%)
> 13, Missing: 104 (34.7%)
> 14, Missing: 106 (35.3%)
> 15, Missing: 247 (82.3%)
> 16, Missing: 102 (34.0%)
> 17, Missing: 118 (39.3%)
> 18, Missing: 29 (9.7%)
> 19, Missing: 33 (11.0%)
> 20, Missing: 165 (55.0%)
> 21, Missing: 198 (66.0%)
> 22, Missing: 1 (0.3%)
> 23, Missing: 0 (0.0%)
> 24, Missing: 0 (0.0%)
> 25, Missing: 0 (0.0%)
> 26, Missing: 0 (0.0%)
> 27, Missing: 0 (0.0%)
Podemos observar que algunas columnas (por ejemplo, los índices de columna 1 y 2) no tienen valores faltantes, mientras que otras columnas (por ejemplo, los índices de columna 15 y 21) tienen muchos o incluso la mayoría de los valores faltantes.
Transformación de Datos con IterativeImputer: Es una transformación de datos configurada según el método utilizado para estimar los valores faltantes. Por defecto, se emplea un modelo
BayesianRidge()que utiliza una función de todas las demás características de entrada. Las características se completan en orden ascendente, desde aquellas con menos valores faltantes hasta aquellas con más.
from numpy import isnan
from pandas import read_csv
from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import IterativeImputer
imputer = IterativeImputer(n_nearest_features=None, imputation_order='ascending')
En la función
IterativeImputer, el parámetron_nearest_features=Nonese usa para especificar cuántas características vecinas considerar al imputar un valor faltante. Al establecerlo enNone, se indica que el algoritmo utilizará todas las características disponibles para estimar el valor faltante.
data = dataframe.values
ix = [i for i in range(data.shape[1]) if i != 23]
X, y = data[:, ix], data[:, 23]
print('Missing: %d' % sum(isnan(X).flatten()))
Missing: 1605
El imputador se ajusta a un conjunto de datos. Luego, el imputador ajustado se aplica a un conjunto de datos para crear una copia del conjunto de datos con todos los valores faltantes de cada columna reemplazados por un valor estimado. La clase
IterativeImputerno se puede utilizar directamente porque es experimental.
imputer = IterativeImputer()
imputer.fit(X)
Xtrans = imputer.transform(X)
print('Missing: %d' % sum(isnan(Xtrans).flatten()))
Missing: 0
IterativeImputer y evaluación de modelos#
Para aplicar correctamente la imputación iterativa de datos faltantes y evitar la fuga de datos, se crea un
pipelinede modelado donde el primer paso sea la imputación iterativa, y el segundo paso sea el modelo. Esto se puede lograr utilizando la clasePipeline. Por ejemplo, elPipelinea continuación utiliza unIterativeImputercon la estrategia predeterminada, seguido de un modelo de bosque aleatorio.Podemos evaluar el conjunto de datos imputado y el
pipelinede modelado de bosque aleatorio para el conjunto de datos con validación cruzada repetida de 10 pliegues.
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.ensemble import RandomForestClassifier
from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import IterativeImputer
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.pipeline import Pipeline
model = RandomForestClassifier()
imputer = IterativeImputer()
pipeline = Pipeline(steps=[('i', imputer), ('m', model)])
url = 'https://raw.githubusercontent.com/lihkir/Data/main/horse-colic.csv'
dataframe = read_csv(url, header=None, na_values='?')
data = dataframe.values
ix = [i for i in range(data.shape[1]) if i != 23]
X, y = data[:, ix], data[:, 23]
model = RandomForestClassifier()
imputer = IterativeImputer()
pipeline = Pipeline(steps=[('i', imputer), ('m', model)])
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
scores = cross_val_score(pipeline, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise')
print('Mean Accuracy: %.3f (%.3f)' % (mean(scores), std(scores)))
Mean Accuracy: 0.870 (0.046)
Recuerde que
StratifiedKFoldgarantiza que cada subconjunto de entrenamiento y prueba tenga una distribución similar de clases. El parámetron_repeats=3enRepeatedStratifiedKFoldindica cuántas veces se repite la validación cruzada estratificada. Esto significa que se ejecutará la validación cruzada estratificada 3 veces, y en cada repetición se utilizarán 10 divisiones diferentes de los datos.En este caso,
error_score='raise'significa que si ocurre algún error durante el ajuste o la evaluación del modelo en un pliegue, se generará una excepción (Exception) y se detendrá el proceso de validación cruzada. Esto ayuda a identificar y abordar problemas potenciales con el modelo o los datos.
Los resultados pueden variar debido a la naturaleza estocástica del algoritmo o del procedimiento de evaluación, o diferencias en la precisión numérica. Considera ejecutar el ejemplo varias veces y comparar el resultado promedio.
El pipeline se evalúa utilizando tres repeticiones de validación cruzada de 10 pliegues y reporta una precisión media de clasificación en el conjunto de datos de aproximadamente 86.3 por ciento, lo cual es un buen puntaje. ¿Cómo sabemos que usar una estrategia iterativa predeterminada es buena o la mejor para este conjunto de datos?
IterativeImputer y diferente orden de imputación#
Por defecto, la imputación se realiza en orden ascendente, desde la característica con menos valores faltantes hasta la característica con más valores faltantes. Sin embargo, podemos experimentar con diferentes estrategias de orden de imputación, como descendente, de derecha a izquierda (árabe), de izquierda a derecha (romano) y aleatorio.
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.ensemble import RandomForestClassifier
from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import IterativeImputer
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.pipeline import Pipeline
from matplotlib import pyplot
dataframe = read_csv(url, header=None, na_values='?')
data = dataframe.values
ix = [i for i in range(data.shape[1]) if i != 23]
X, y = data[:, ix], data[:, 23]
results = list()
strategies = ['ascending', 'descending', 'roman', 'arabic', 'random']
for s in strategies:
pipeline = Pipeline(steps=[('i', IterativeImputer(imputation_order=s)), ('m', RandomForestClassifier())])
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
scores = cross_val_score(pipeline, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
results.append(scores)
print('>%s %.3f (%.3f)' % (s, mean(scores), std(scores)))
>ascending 0.862 (0.054)
>descending 0.870 (0.051)
>roman 0.872 (0.052)
>arabic 0.876 (0.048)
>random 0.868 (0.056)
pyplot.boxplot(results, labels=strategies, showmeans=True)
pyplot.xticks(rotation=45)
pyplot.show()
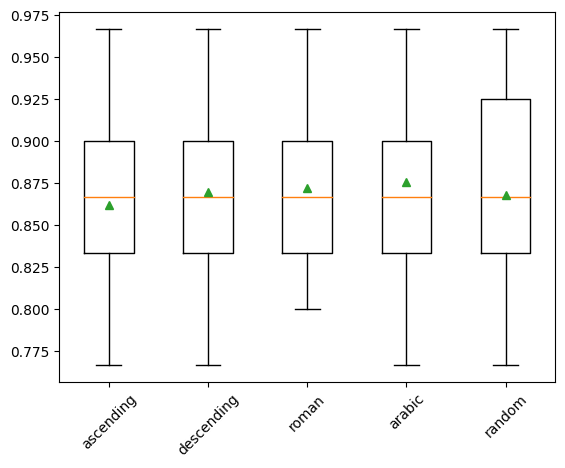
Los resultados sugieren pocas diferencias entre la mayoría de los métodos, con el orden descendente (opuesto al predeterminado) obteniendo el mejor rendimiento. Los resultados sugieren que el orden árabe (de derecha a izquierda) o romano podría ser mejor para este conjunto de datos con una precisión de aproximadamente 87.2 por ciento.
IterativeImputer y diferente número de iteraciones#
Por defecto,
IterativeImputerrepetirá el número de iteraciones 10 veces. Es posible que un gran número de iteraciones comience a sesgar o distorsionar la estimación y que se prefieran pocas iteraciones. El número de iteraciones del procedimiento se puede especificar mediante el argumento"max_iter". El siguiente ejemplo compara diferentes valores para"max_iter"desde 1 hasta 20.
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.ensemble import RandomForestClassifier
from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import IterativeImputer
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.pipeline import Pipeline
from matplotlib import pyplot
dataframe = read_csv(url, header=None, na_values='?')
data = dataframe.values
ix = [i for i in range(data.shape[1]) if i != 23]
X, y = data[:, ix], data[:, 23]
results = list()
strategies = [str(i) for i in range(1, 21)]
for s in strategies:
pipeline = Pipeline(steps=[('i', IterativeImputer(max_iter=int(s))), ('m', RandomForestClassifier())])
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
scores = cross_val_score(pipeline, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
results.append(scores)
print('>%s %.3f (%.3f)' % (s, mean(scores), std(scores)))
>1 0.869 (0.049)
>2 0.879 (0.051)
>3 0.872 (0.054)
>4 0.866 (0.053)
>5 0.869 (0.054)
>6 0.873 (0.051)
>7 0.869 (0.052)
>8 0.877 (0.050)
>9 0.872 (0.053)
>10 0.877 (0.050)
>11 0.878 (0.051)
>12 0.869 (0.050)
>13 0.870 (0.053)
>14 0.872 (0.055)
>15 0.867 (0.051)
>16 0.869 (0.050)
>17 0.864 (0.046)
>18 0.871 (0.055)
>19 0.870 (0.051)
>20 0.871 (0.053)
pyplot.boxplot(results, labels=strategies, showmeans=True)
pyplot.xticks(rotation=45)
pyplot.show()
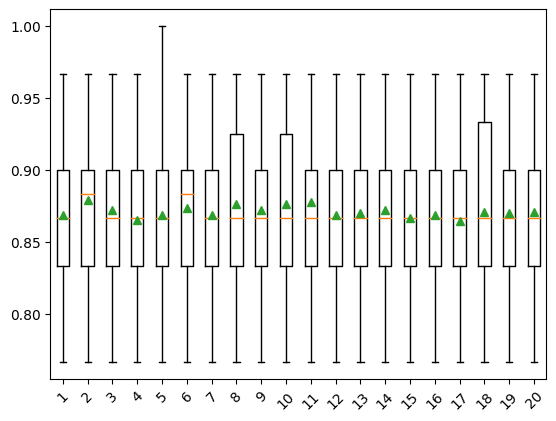
Los resultados sugieren que muy pocas iteraciones, como 3, podrían ser igual de efectivas o más que 9-12 iteraciones en este conjunto de datos.
IterativeImputer al hacer una predicción#
Podemos desear crear un
pipelinede modelado final con la imputación iterativa y el algoritmo de bosque aleatorio, y luego hacer una predicción para nuevos datos. Esto se puede lograr definiendo elpipeliney ajustándolo en todos los datos disponibles, luego llamando a la funciónpredict(), pasando los nuevos datos como argumento. Es importante destacar que la fila de nuevos datos debe marcar cualquier valor faltante utilizando el valorNaN.
from numpy import nan
dataframe = read_csv(url, header=None, na_values='?')
data = dataframe.values
X, y = data[:, :-1], data[:, -1]
pipeline = Pipeline(steps=[('i', IterativeImputer()), ('m', RandomForestClassifier())])
pipeline.fit(X, y)
Pipeline(steps=[('i', IterativeImputer()), ('m', RandomForestClassifier())])In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
Pipeline(steps=[('i', IterativeImputer()), ('m', RandomForestClassifier())])IterativeImputer()
RandomForestClassifier()
row = [2, 1, 530101, 38.50, 66, 28, 3, 3, nan, 2, 5, 4, 4, nan, nan, nan, 3, 5, 45.00, 8.40, nan, nan, 2, 11300, 00000, 00000, 2]
yhat = pipeline.predict([row])
print('Predicted Class: %d' % yhat[0])
Predicted Class: 1
Instancias y/o funciones duplicadas#
El tercer problema es la presencia de instancias y/o características duplicadas en un conjunto de datos. Se trata de elementos innecesarios en el conjunto de datos y, si no se eliminan, pueden afectar a las tendencias y a los conocimientos que se muestran en una visualización.
Por ejemplo, puede crear una visualización que muestre la relación entre el género de un adolescente y si toca el piano. Con un conjunto de datos sin valores atípicos, anomalías o valores perdidos, obtendrá una gran visualización.
A partir de la visualización, podrá también concluir que hay más mujeres que tocan el piano que hombres. Sin embargo, digamos que la visualización proviene del conjunto de datos siguiente
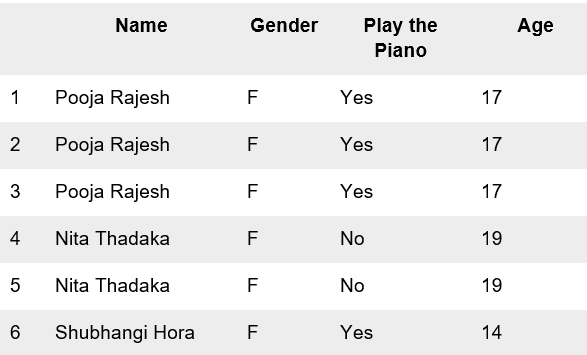
Hay dos instancias para Nita Thadaka y tres instancias para Pooja Rajesh, lo que significa que hay tres instancias duplicadas en total. Esto significa que la información que la visualización está proporcionando es inexacta. La forma de tratar los duplicados es sencilla: eliminarlos. Con este fin puede utlizar la función:
.drop_duplicates()
Mala selección de características#
Con respecto a un conjunto de datos, una característica es una columna en el conjunto de datos, mientras que una instancia es una fila en el conjunto de datos. Por ejemplo, en la tabla anterior, nombre, sexo, tocar el piano y la edad son características, mientras que Pooja Rajesh, F, Yes y 17 es una instancia.
Dado que el objetivo de una visualización es mostrar una tendencia, un patrón, una relación o algún vínculo entre dos o más características en un conjunto de datos, es importante que la selección de esas características se haga con cuidado. Por lo tanto, este es un punto crucial en la visualización de datos.
Si el objetivo es transmitir que existe una fuerte relación entre dos características, entonces hay que asegurarse de que están fuertemente correlacionadas antes de proceder a su visualización. La selección de características insignificantes dará lugar a una visualización sin sentido y no transmitirá ninguna información concreta. Por ejemplo, en cuanto al conjunto de datos co2.csv, el conjunto de datos contiene información sobre las emisiones de dióxido de carbono por país y el PIB por país. Comprobamos la correlación entre las emisiones de CO2 y el PIB antes de visualizar el conjunto de datos, garantizando que íbamos a crear una una visualización que valiera la pena.
Ejercicio para entregar#
Determine las características que se visualizan en un gráfico de dispersión. Se le da el conjunto de datos co2.csv y se le pide que proporcione información sobre él, como por ejemplo, qué tipo de patrones existen, si hay tendencias entre las características, etc. Es necesario que su visualización final transmita información significativa. Para conseguirlo, va a crear visualizaciones para diferentes emparejamientos de características para entender están correlacionadas y, por lo tanto, vale la pena visualizarlas.
Pasos principales
Importe las bibliotecas necesarias.
Vuelva a crear el
DataFrame. Desde elDataFramegm incluya las columnaspopulation,fertility, ylifeVisualiza la relación entre el
co2ylifeutilizando un gráfico de dispersión, con el nombre del país como información en la herramienta hover y el año como deslizador.Comprueba la correlación entre
co2ylife.Visualiza la relación entre
co2yfertilitymediante un gráfico de dispersión, con el nombre del país como información en la herramienta hover y el año como deslizador.Comprueba la correlación entre
co2yfertility
Realicé un EDA para el siguiente conjunto de datos (ver Diabetes Dataset). El conjunto de datos consta de varias variables médicas predictoras (independientes) y una variable objetivo (diagnóstico, dependiente), resultado. Las variables independientes incluyen el número de embarazos que ha tenido la paciente, BMI (
Body mass index(peso enkg/(height in m)^2), nivel de insulina, edad, etc. En este dataset, sustituimos todos los valores nulos “faltantes” por NAN y realizamos el respectivo análisis de datos faltantes.
df.loc[df["Glucose"] == 0.0, "Glucose"] = np.NAN
df.loc[df["BloodPressure"] == 0.0, "BloodPressure"] = np.NAN
df.loc[df["SkinThickness"] == 0.0, "SkinThickness"] = np.NAN
df.loc[df["Insulin"] == 0.0, "Insulin"] = np.NAN
df.loc[df["BMI"] == 0.0, "BMI"] = np.NAN
Aplique imputación de datos usando las diferentes opciones de estimadores (ver iterative-imputer-variants-comparison). Identifique si el problema es de clasificación o regresión previamente.
Identifique datos atípicos para cada variable en el dataset usando las técnicas estudiadas en clase. Además, realice imputación de los datos atípicos con base en lo desarrollado en el ítem anterior (ver IterativeImputer).
Imputación/Capping/Predicción
Use los siguientes tests para detectar valores atípicos: Test de Rosner, Dixon, Grubbs, Hampel, Percentiles, Boxplots, Histograms, Descriptivos
