1. Introducción a las Series de Tiempo

• En esta sección se presentan algunos métodos estadísticos básicos, los cuales son esenciales para modelar, analizar y predecir datos de series temporales. Se presentan gráficos y resúmenes numéricos de las propiedades de los datos de series temporales. También se analiza el uso de transformaciones y ajustes de datos en la predicción y algunos métodos ampliamente utilizados para caracterizar y controlar el rendimiento de un modelo predictivo.

• Algunos aspectos de como las medidas de rendimiento pueden usarse para seleccionar entre técnicas de predicción son presentados. Las predicciones se basan en datos u observaciones sobre la variable de interés. Estos datos suelen adoptar la forma de una serie temporal.

1.1. Diferentes tipos de datos

Los analistas de negocio y científicos de datos se encuentran con diferentes tipos de datos en sus proyectos de análisis. La mayoría de los datos que se suelen encontrar en proyectos académicos e industriales se pueden clasificar a grandes rasgos en las siguientes categorías:

• Datos transversales

• Datos de series temporales

• Datos de panel

Comprender qué tipo de datos se necesitan para resolver un problema y qué tipo de datos pueden obtenerse de las fuentes disponibles es importante para formular el problema y elegir el tipo de modelo más adecuado.

1.2. Datos transversales

• Los datos transversales o de corte transversal de una población se obtienen tomando observaciones de múltiples individuos en el mismo momento. Los datos transversales pueden incluir observaciones tomadas en distintos momentos, pero en estos casos el tiempo no desempeña ningún papel significativo en el análisis. Los resultados de la selectividad de los estudiantes es un ejemplo de datos transversales. El producto interno bruto de los países y los datos para el análisis de pérdida de clientes es otro ejemplo de datos transversales.

Observación

• En esencia, los datos transversales representan un instante o momento dado. Sin embargo, los datos de clientes para el análisis de rotación pueden obtenerse a lo largo de un periodo de tiempo, como años y meses. Pero, a efectos de análisis, el tiempo puede no desempeñar un papel importante y, por lo tanto, aunque los datos de rotación de clientes pueden obtenerse de múltiples puntos en el tiempo, pueden seguir considerándose como un conjunto de datos transversal.

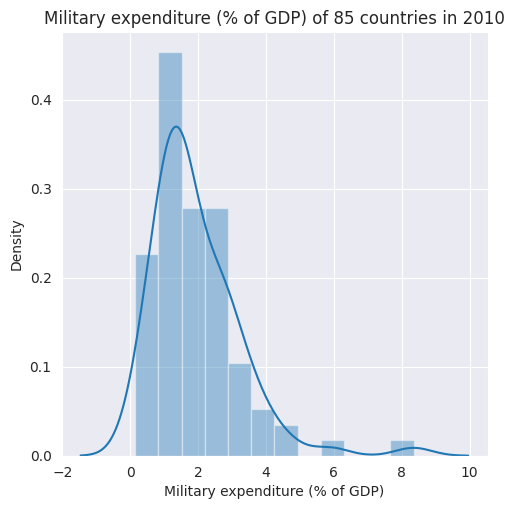
• A menudo, el análisis de datos transversales comienza con un gráfico de las variables, para visualizar sus propiedades estadísticas como la tendencia central, la dispersión, la asimetría y la curtosis. En el siguiente ejemplo univariado se muestra el Gasto militar como porcentaje del Producto Interno Bruto de 85 países en el año 2010. Los datos usados en el presente curso se encuentran en el repositorio Dataset for TSF.

• Al tomar los datos de un solo año aseguramos su naturaleza transversal. La figura combina un histograma normalizado y un gráfico de densidad de kernel para resaltar las diferentes propiedades estadísticas de los datos de gasto militar. Utilizaremos seaborn en este caso para realizar las visualizaciones. Para temas diferentes al seleccionado (ver seaborn templates). Para descargar todos los datos que serán utilizados en este curso (ver Dataset for TSF)

import warnings
warnings.filterwarnings("ignore")

import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns

sns.set_style("darkgrid")

data = pd.read_csv('/home/lihkir/Data/WDIData.csv')
print('Column names:', data.columns)

Column names: Index(['Country Name', 'Country Code', 'Indicator Name', 'Indicator Code',
       '1960', '1961', '1962', '1963', '1964', '1965', '1966', '1967', '1968',
       '1969', '1970', '1971', '1972', '1973', '1974', '1975', '1976', '1977',
       '1978', '1979', '1980', '1981', '1982', '1983', '1984', '1985', '1986',
       '1987', '1988', '1989', '1990', '1991', '1992', '1993', '1994', '1995',
       '1996', '1997', '1998', '1999', '2000', '2001', '2002', '2003', '2004',
       '2005', '2006', '2007', '2008', '2009', '2010', '2011', '2012', '2013',
       '2014', '2015', '2016', 'Unnamed: 61'],
      dtype='object')

• También podemos hacernos una idea del tamaño de los datos en número de filas y columnas ejecutando la siguiente línea

print('No. of rows, columns:', data.shape)

No. of rows, columns: (401016, 62)

• Este conjunto de datos tiene, 401016 filas porque recoge indicadores de desarrollo mundial para cada país. Esta información sobre el número único de indicadores y países puede obtenerse ejecutando las líneas siguientes

nb_countries = data['Country Code'].unique().shape[0]
print('Unique number of countries:', nb_countries)

Unique number of countries: 264

• Como se desprende de la estructura de los datos, cada fila ofrece las observaciones sobre un indicador, que se identifica mediante las columnas Indicator Name y Indicator Code, y sobre el país, que se indica mediante las columnas Country Name y Country Code.

data.dtypes

Country Name       object
Country Code       object
Indicator Name     object
Indicator Code     object
1960              float64
                   ...   
2013              float64
2014              float64
2015              float64
2016              float64
Unnamed: 61       float64
Length: 62, dtype: object

• Las columnas de 1960 a 2016 tienen los valores de un indicador durante el mismo periodo de tiempo. En esta comprensión de cómo se disponen los datos en el DataFrame, ahora estamos preparados para extraer las filas y columnas que son relevantes para nuestra visualización.

• Comencemos preparando otros dos DataFrame que obtengan las filas correspondientes a los indicadores Total Central Government Debt (as % of GDP) y Military expenditure (% of GDP) para todos los países. Esto se hace por medio del DataFrame original de la siguiente manera

central_govt_debt = data.loc[data['Indicator Name']=='Central government debt, total (% of GDP)']
military_exp = data.loc[data['Indicator Name']=='Military expenditure (% of GDP)']

• Las dos líneas anteriores crean dos nuevos DataFrame, a saber, central_govt_debt y militar_exp. Una comprobación rápida de la forma de estos DataFrame puede hacerse ejecutando las dos líneas siguientes

print('Shape of central_govt_debt:', central_govt_debt.shape)
print('Shape of military_exp:', military_exp.shape)

Shape of central_govt_debt: (264, 62)
Shape of military_exp: (264, 62)

• Estos DataFrame contienen toda la información que necesitamos. Para trazar los datos univariantes y transversales necesitaremos la columna 2010. Antes de ejecutar el código para el trazado, comprobemos rápidamente si falta la columna 2010. Esto se hace mediante las dos líneas siguientes

central_govt_debt['2010'].describe()

count     94.000000
mean      53.048479
std       29.790674
min        0.519665
25%       28.357797
50%       49.540245
75%       75.259012
max      161.596402
Name: 2010, dtype: float64

military_exp['2010'].describe()

count    192.000000
mean       1.988556
std        1.354856
min        0.000000
25%        1.190287
50%        1.613407
75%        2.624711
max        8.565679
Name: 2010, dtype: float64

• Además, queremos que la columna Country Code sea el índice de las filas. Así que se ejecuta el siguiente par de líneas

central_govt_debt.index = central_govt_debt['Country Code']
military_exp.index = military_exp['Country Code']

• A continuación, creamos dos pandas.Series tomando columnas 2010 no vacías de central_govt_debt y military_exp. Los objetos Series recién creados se unifican para formar un único DataFrame

central_govt_debt_2010 = central_govt_debt['2010'].loc[~pd.isnull(central_govt_debt['2010'])]
military_exp_2010 = military_exp['2010'].loc[~pd.isnull(military_exp['2010'])]

central_govt_debt_2010

Country Code
CEB    47.446156
EMU    72.414709
ECS    63.137736
ECA    22.338687
TEC    27.287492
         ...    
UGA    27.552595
UKR    29.969556
GBR    83.406797
USA    85.601594
URY    44.222702
Name: 2010, Length: 94, dtype: float64

military_exp_2010

Country Code
ARB    5.117807
CEB    1.482543
EAR    2.335511
EAS    1.563325
EAP    1.724963
         ...   
VEN    0.853924
VNM    2.305049
YEM    4.685557
ZMB    1.382593
ZWE    0.977841
Name: 2010, Length: 192, dtype: float64

data_to_plot = pd.concat((central_govt_debt_2010, military_exp_2010), axis=1)
data_to_plot.columns = ['central_govt_debt', 'military_exp']

data_to_plot.head()

	central_govt_debt	military_exp
Country Code
CEB	47.446156	1.482543
EMU	72.414709	1.618759
ECS	63.137736	1.860343
ECA	22.338687	2.933044
TEC	27.287492	2.785617

data_to_plot.shape

(202, 2)

• Podemos visualizar, por ejemplo, el top 10 de países con mayor Central government debt, total (% of GDP). Nótese que la cantidad real invertida, va a depender de que tan grande es ese porcentaje GDP, y está fijada de manera transversal al año 2010.

df_ordenado = data_to_plot.sort_values(by='military_exp', ascending=False)
df_ordenado.head(10)

	central_govt_debt	military_exp
Country Code
SAU	NaN	8.565679
OMN	5.039094	8.347635
ISR	NaN	6.228475
ARE	NaN	6.038592
JOR	61.373457	5.895421
TCD	NaN	5.778139
ARB	NaN	5.117807
MEA	NaN	4.804054
YEM	NaN	4.685557
USA	85.601594	4.665615

• Para graficar, tenemos que tomar solo aquellos países que tienen las columnas central_govt_debt y military_exp diferentes de cero. Ejecute la línea siguiente para filtrar las filas con valores omitidos

data_to_plot = data_to_plot.loc[(~pd.isnull(data_to_plot.central_govt_debt)) & (~pd.isnull(data_to_plot.military_exp)), :]

data_to_plot.head()

	central_govt_debt	military_exp
Country Code
CEB	47.446156	1.482543
EMU	72.414709	1.618759
ECS	63.137736	1.860343
ECA	22.338687	2.933044
TEC	27.287492	2.785617

data_to_plot.shape

(84, 2)

• La tabla anterior solo tiene valores no vacíos y ya estamos listos para generar los gráficos para los datos transversales. Las siguientes líneas de código generan el gráfico de los datos univariantes transversales sobre el gasto militar

• Podemos visualizar, por ejemplo, el top 10 de países con mayor Central government debt, total (% of GDP). Nótese que la cantidad real invertida, va a depender de que tan grande es ese porcentaje GDP, y está fijada de manera transversal al año 2010.

df_ordenado = data_to_plot.sort_values(by='military_exp', ascending=False)
df_ordenado.head(10)

	central_govt_debt	military_exp
Country Code
OMN	5.039094	8.347635
JOR	61.373457	5.895421
USA	85.601594	4.665615
NAC	82.576224	4.328041
GEO	36.799720	3.902453
RUS	9.098114	3.850719
COL	72.337793	3.631149
NAM	16.944972	3.514744
SGP	102.903421	3.429849
MAR	50.962499	3.390796

• Podemos visualizar, por ejemplo, el top 10 de países con mayor Central government debt, total (% of GDP). Nótese que la cantidad real invertida, va a depender de que tan grande es ese porcentaje GDP, y está fijada de manera transversal al año 2010.

df_ordenado = data_to_plot.sort_values(by='military_exp', ascending=False)
df_ordenado.head(10)

	central_govt_debt	military_exp
Country Code
OMN	5.039094	8.347635
JOR	61.373457	5.895421
USA	85.601594	4.665615
NAC	82.576224	4.328041
GEO	36.799720	3.902453
RUS	9.098114	3.850719
COL	72.337793	3.631149
NAM	16.944972	3.514744
SGP	102.903421	3.429849
MAR	50.962499	3.390796

• Realizamos algunos tests de normalidad por ejemplo para military expenditure

military_exp_np = np.array(data_to_plot.military_exp)

plt.figure(figsize=(5.5, 5.5))
g = sns.distplot(military_exp_np, norm_hist=False)
g.set_title('Military expenditure (% of GDP) of 85 countries in 2010');
plt.xlabel("Military expenditure (% of GDP)");

from statsmodels.graphics.gofplots import qqplot
qqplot(military_exp_np, line='s');

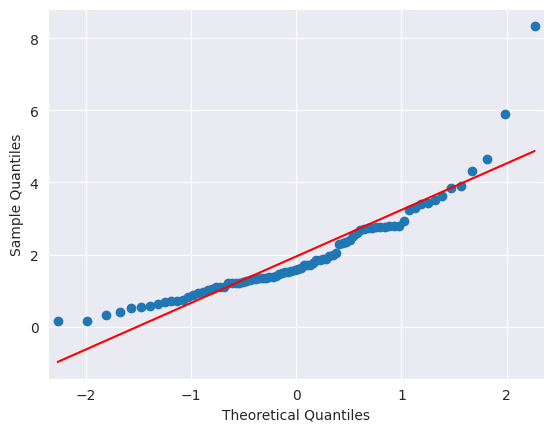
Prueba de Shapiro-Wilk y Kolmogorov-Smirnov

• La prueba de Shapiro-Wilk evalúa una muestra de datos y cuantifica la probabilidad de que los datos procedan de una distribución gaussiana, en honor a Samuel Shapiro y Martin Wilk. En la práctica, se cree que la prueba de Shapiro-Wilk es una prueba fiable de normalidad, aunque hay algunos indicios de que la prueba puede ser adecuada para muestras de datos más pequeñas (\(n < 50\) idealmente), por ejemplo, miles de observaciones o menos.

• El test de Kolmogorov-Smirnov (KS) es menos afectado por el tamaño muestral en comparación con el test de Shapiro-Wilk. Por lo tanto, puede ser más apropiado para muestras grandes, donde el test de Shapiro-Wilk tiende a volverse más conservador. El test de KS es más general y no se limita únicamente a la normalidad. Puede utilizarse para comparar cualquier distribución empírica con una distribución teórica.

• La función shapiro() SciPy calcula la prueba de Shapiro-Wilk (ver Shapiro-Wilk test) en un conjunto de datos determinado. La función devuelve tanto el estadístico \(W\) calculado por la prueba como el \(p\)-value. A continuación se muestra el ejemplo completo de realización de la prueba de Shapiro-Wilk en el conjunto de datos.

\[\begin{split} \begin{align*} H_{0}&:\quad\textsf{La variable presenta una distribución normal}\\ H_{1}&:\quad\textsf{La variable presenta una distribución no normal} \end{align*} \end{split}\]

from scipy.stats import shapiro

print('Shapiro-Wilk Test:')
stat, p = shapiro(military_exp_np)
print('Statistics=%.6f, p=%e' % (stat, p))

alpha = 0.05
if p > alpha:
 print('Sample looks Normal (fail to reject H0)')
else:
 print('Sample does not look Normal (reject H0)')

Shapiro-Wilk Test:
Statistics=0.857023, p=1.646573e-07
Sample does not look Normal (reject H0)

import numpy as np
from scipy import stats

print('Kolmogorov-Smirnov:')
stat, p = stats.kstest(military_exp_np, stats.norm.cdf)
print('Statistics=%.6f, p=%e' % (stat, p))

alpha = 0.05
if p > alpha:
 print('Sample looks Normal (fail to reject H0)')
else:
 print('Sample does not look Normal (reject H0)')

Kolmogorov-Smirnov:
Statistics=0.659326, p=2.320049e-36
Sample does not look Normal (reject H0)

Prueba \(K^2\) de D'Agostino

• La prueba \(K^2\) de D’Agostino calcula los estadísticos de resumen de los datos, es decir, la curtosis y la asimetría, para determinar si la distribución de los datos se aparta de la distribución normal, llamada así por Ralph D'Agostino. La asimetría (skew) es una cuantificación del grado en que una distribución se desplaza hacia la izquierda o hacia la derecha, es una medida de la asimetría de la distribución.

• La curtosis (kurtosis) cuantifica la proporción de la distribución que se encuentra en cierta cola lateral (ver Fig. 1.1). Es una prueba estadística de normalidad sencilla y de uso común. La prueba \(K^2\) de D’Agostino está disponible a través de la función SciPy normaltest() y devuelve el estadístico de la prueba y el \(p\)-value

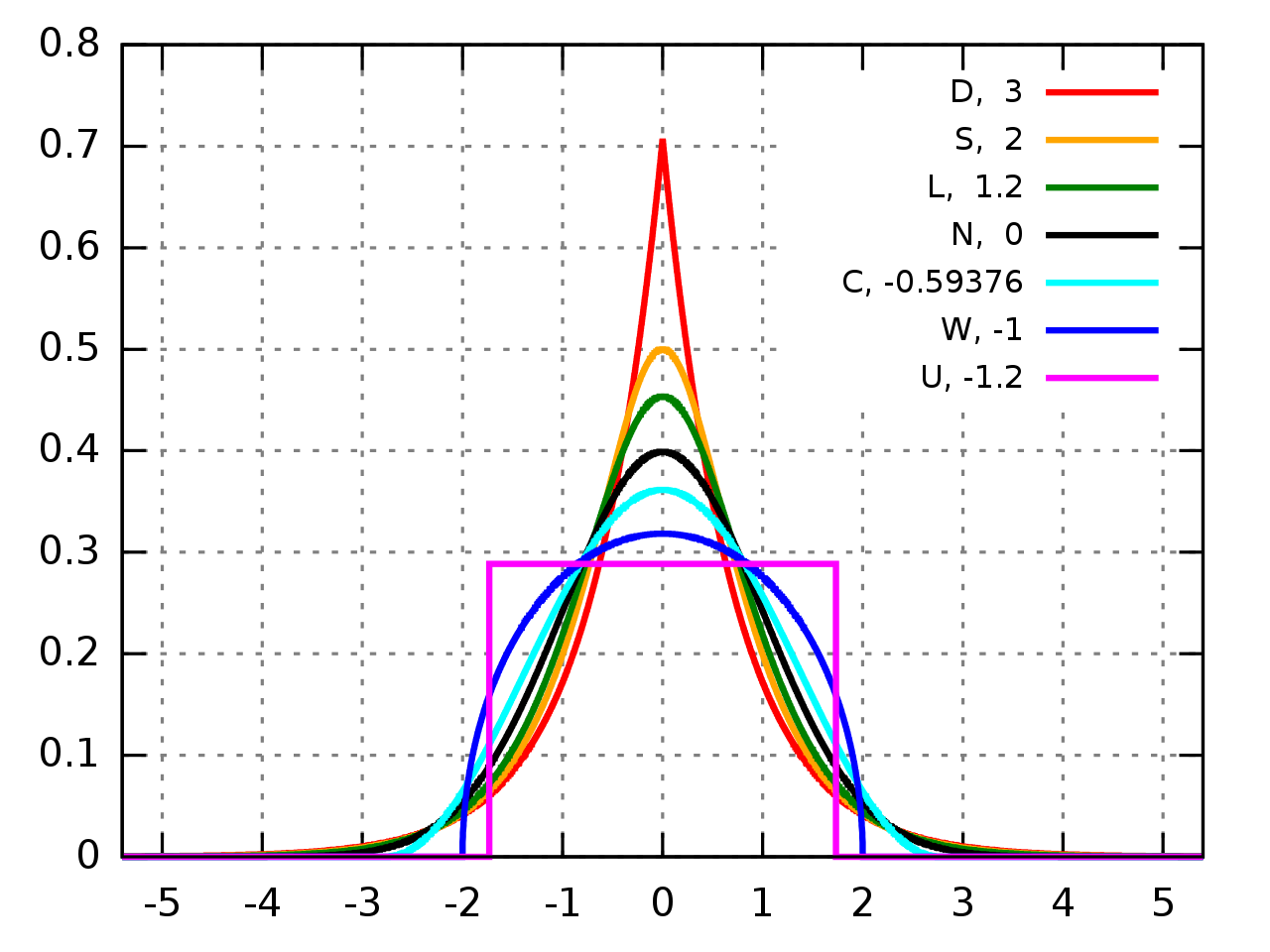
Fig. 1.1 Diferentes distribuciones asociadas a multiples valores de kurtosis. Fuente wikipedia.

• D: Distribución de Laplace (kurtosis = 3);

• S: Distribución hiperbólica secante, (kurtosis = 2);

• L: Distribución logística, (kurtosis = 1.2);

• N: Distribución normal, (kurtosis = 0);

• C: Distribución del coseno elevado, (kurtosis = -0,593762);

• W: Distribución del semicírculo de Wigner, (kurtosis = -1);

• U: Distribución uniforme, (kurtosis = -1.2).

from scipy.stats import normaltest, kurtosis, skew

stat, p = normaltest(military_exp_np)
print('Statistics=%.3f, p=%.3f' % (stat, p))

alpha = 0.05
if p > alpha:
 print('Sample looks Gaussian (fail to reject H0)')
else:
 print('Sample does not look Gaussian (reject H0)')

print('Kurtosis=%.3f'%kurtosis(military_exp_np))
print('Skew=%.3f'%skew(military_exp_np))

Statistics=49.874, p=0.000
Sample does not look Gaussian (reject H0)
Kurtosis=6.122
Skew=1.916

Observación

• Kurtosis mayor que 0: Indica una distribución leptocúrtica, lo que significa que la distribución tiene colas más pesadas y es más puntiaguda en comparación con una distribución normal. Esto implica que hay una mayor concentración de datos alrededor de la media, con valores extremos más frecuentes.

• Kurtosis menor que 0: Indica una distribución platicúrtica, lo que significa que la distribución es más aplanada y tiene colas más ligeras en comparación con una distribución normal. Esto implica que los datos están más dispersos y hay menos valores en la región de la media, con valores extremos menos frecuentes.

1.3. Datos de series temporales

Introducción

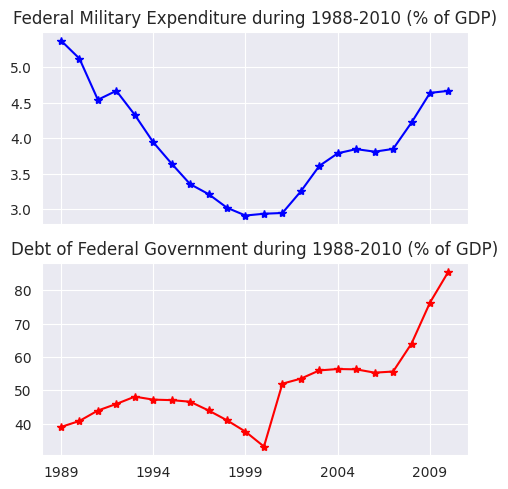
• El ejemplo de datos transversales comentado anteriormente corresponde únicamente al año 2010. Sin embargo, en cambio, si consideramos un solo país, por ejemplo Estados Unidos (USA), y echamos un vistazo a sus Federal Military Expenditure, Debt of Federal Government, durante un periodo de 10 años, de 2001 a 2010, obtendríamos dos series temporales:

  • Federal Military Expenditure

  • Debt of Federal Government

• Por lo tanto, en esencia, una serie temporal se compone de observaciones cuantitativas sobre una o más características medibles de una entidad individual y tomadas en múltiples puntos en el tiempo. En este caso, los datos representan Federal Military Expenditure, Debt of Federal Government.

• Los datos de series temporales suelen caracterizarse por varias estructuras internas interesantes, como la tendencia, la estacionalidad, estacionariedad, autocorrelación, etc. Las estructuras internas de los datos de series temporales requieren una formulación y técnicas especiales para su análisis. Estas técnicas se tratarán en los siguientes capítulos con estudios de casos e implementación de código de trabajo en Python.

• Para generar los gráficos anteriores usaremos el código que se desarrolló para obtener los gráficos para los datos transversales. Comenzaremos creando dos nuevas series para representar las series temporales de Federal Military Expenditure y Debt of Federal Government, desde 1960 hasta 2010

central_govt_debt_us = central_govt_debt.loc[central_govt_debt['Country Code']=='USA', :].T
military_exp_us = military_exp.loc[military_exp['Country Code']=='USA', :].T

• Los dos objetos Series creados en el código anterior se fusionan para formar un único DataFrame y se cortan para contener los datos de los años 2001 a 2010:

data_us = pd.concat((military_exp_us, central_govt_debt_us), axis=1)
index0 = np.where(data_us.index=='1960')[0][0]
index1 = np.where(data_us.index=='2010')[0][0]
data_us = data_us.iloc[index0:index1+1,:]
data_us.columns = ['Federal Military Expenditure', 'Debt of Federal Government']
data_us.head()

	Federal Military Expenditure	Debt of Federal Government
1960	8.35266	NaN
1961	8.487129	NaN
1962	8.656586	NaN
1963	8.189007	NaN
1964	7.467629	NaN

• Podemos utilizar los métodos isna() o isnull() para contabilizar datos faltantes en los datos. Podemos obtener el total de valores perdidos en cada columna con la función sum() o tomar la media con mean(). Técnicas de imputación de datos faltantes pueden ser utilizadas del módulo de Visualización de Datos

data_us.isna().sum()

Federal Military Expenditure     0
Debt of Federal Government      29
dtype: int64

(data_us.isnull().sum()/len(data_us))*100

Federal Military Expenditure     0.000000
Debt of Federal Government      56.862745
dtype: float64

data_us['backward_fill'] = data_us['Debt of Federal Government'].bfill()
data_us.head()

	Federal Military Expenditure	Debt of Federal Government	backward_fill
1960	8.35266	NaN	39.016963
1961	8.487129	NaN	39.016963
1962	8.656586	NaN	39.016963
1963	8.189007	NaN	39.016963
1964	7.467629	NaN	39.016963

• El método .bfill() en Pandas se utiliza para rellenar los valores faltantes (NaN) en una Serie o DataFrame hacia atrás (backward fill). Por ejemplo, si tiene una columna con valores [1, NaN, 3, NaN, 5], al aplicar .bfill(), los valores faltantes se llenarán con los valores siguientes más cercanos, dando como resultado [1, 3, 3, 5, 5].

data_us['mean_fill'] = data_us['Debt of Federal Government'].mean()
data_us.head()

	Federal Military Expenditure	Debt of Federal Government	backward_fill	mean_fill
1960	8.35266	NaN	39.016963	51.155537
1961	8.487129	NaN	39.016963	51.155537
1962	8.656586	NaN	39.016963	51.155537
1963	8.189007	NaN	39.016963	51.155537
1964	7.467629	NaN	39.016963	51.155537

data_us['median_fill'] = data_us['Debt of Federal Government'].median()
data_us.head()

	Federal Military Expenditure	Debt of Federal Government	backward_fill	mean_fill	median_fill
1960	8.35266	NaN	39.016963	51.155537	47.659404
1961	8.487129	NaN	39.016963	51.155537	47.659404
1962	8.656586	NaN	39.016963	51.155537	47.659404
1963	8.189007	NaN	39.016963	51.155537	47.659404
1964	7.467629	NaN	39.016963	51.155537	47.659404

data_us['quadratic_fill'] = data_us['Debt of Federal Government'].interpolate(option='quadratic')
data_us.head()

	Federal Military Expenditure	Debt of Federal Government	backward_fill	mean_fill	median_fill	quadratic_fill
1960	8.35266	NaN	39.016963	51.155537	47.659404	NaN
1961	8.487129	NaN	39.016963	51.155537	47.659404	NaN
1962	8.656586	NaN	39.016963	51.155537	47.659404	NaN
1963	8.189007	NaN	39.016963	51.155537	47.659404	NaN
1964	7.467629	NaN	39.016963	51.155537	47.659404	NaN

• El método interpolate() en Pandas se utiliza para interpolar los valores faltantes en una Serie o DataFrame. Al especificar option='quadratic', está indicando que desea utilizar la interpolación cuadrática para llenar los valores faltantes.

• Existen otras técnicas de imputación de datos, tales como por ejemplo: sklearn.impute.KNNImputer, IterativeImputer, etc.,… Nótese que la columna quadratic_fill mantiene los valores NaN. Esta técnica ofrece las siguientes versiones de imputación: 'nearest', 'zero', 'slinear', 'quadratic', 'cubic', 'spline', 'barycentric', 'polynomial' las cuales se le invita a revisar en la documentación. Realice para cada imputación una representación de su nueva distribución e identifique si esta se vio realmente afectada.

• Dado que el cuadro anterior muestra que no se dispone solamente de datos sobre Debt of Federal Government de varios años a partir de 1960, y se necesitan las dos dimensiones, otra opción es eliminar las filas con datos faltantes del Dataframe, data_us antes de trazar la serie temporal

data_us.dropna(inplace=True)
print('Shape of data_us:', data_us.shape)

Shape of data_us: (22, 6)

data_us.head(10)

	Federal Military Expenditure	Debt of Federal Government	backward_fill	mean_fill	median_fill	quadratic_fill
1989	5.374717	39.016963	39.016963	51.155537	47.659404	39.016963
1990	5.120252	40.821367	40.821367	51.155537	47.659404	40.821367
1991	4.539845	43.948026	43.948026	51.155537	47.659404	43.948026
1992	4.666265	45.916542	45.916542	51.155537	47.659404	45.916542
1993	4.326925	48.104749	48.104749	51.155537	47.659404	48.104749
1994	3.941287	47.21406	47.214060	51.155537	47.659404	47.21406
1995	3.638489	47.059783	47.059783	51.155537	47.659404	47.059783
1996	3.350744	46.585511	46.585511	51.155537	47.659404	46.585511
1997	3.209903	43.958801	43.958801	51.155537	47.659404	43.958801
1998	3.017636	41.009914	41.009914	51.155537	47.659404	41.009914

• Por último, las series temporales se generan ejecutando el siguiente código

f, axarr = plt.subplots(2, sharex=True)
f.set_size_inches(5.5, 5.5)
axarr[0].set_title('Federal Military Expenditure during 1988-2010 (% of GDP)')
data_us['Federal Military Expenditure'].plot(linestyle='-', marker='*', color='b', ax=axarr[0])
axarr[1].set_title('Debt of Federal Government during 1988-2010 (% of GDP)')
data_us['Debt of Federal Government'].plot(linestyle='-', marker='*', color='r', ax=axarr[1]);

1.4. Datos de panel

Introducción

• Hemos visto datos transversales (de múltiples individuos en un solo punto en el tiempo) y series temporales (de una entidad a lo largo de múltiples puntos en el tiempo). Si observamos múltiples entidades a lo largo de múltiples puntos en el tiempo, obtenemos un panel de datos o datos longitudinales.

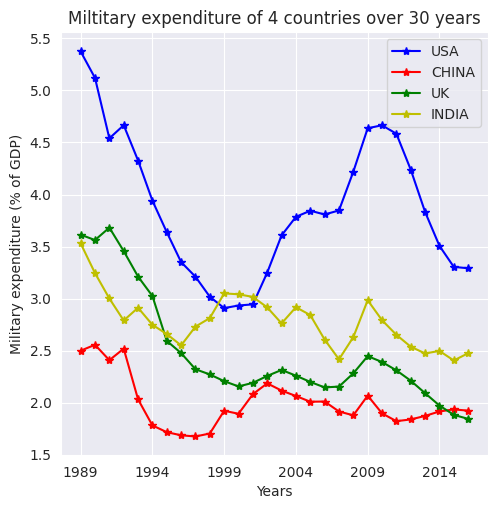
• Tomando como ejemplo para cuatro países 'Military expenditure (% of GDP)' durante el periodo 1960-2010, creamos un conjunto de datos de panel. Ahora, prepararemos los datos para trazar la figura correspondiente, siguiendo un proceso similar al utilizado para los datos transversales y de series temporales en este capítulo.

• Preparemos los datos necesarios para trazar la figura correspondiente. Seguiremos el código que hemos utilizado para los datos transversales y de series temporales en este capítulo. Empezaremos creando un DataFrame con los datos de las cuatro empresas mencionadas en el gráfico anterior. Esto se hace de la siguiente manera:

chn = data.loc[(data['Indicator Name']=='Military expenditure (% of GDP)') & \
               (data['Country Code']=='CHN'), :] #China
chn.head()

	Country Name	Country Code	Indicator Name	Indicator Code	1960	1961	1962	1963	1964	1965	...	2008	2009	2010	2011	2012	2013	2014	2015	2016	Unnamed: 61
134507	China	CHN	Military expenditure (% of GDP)	MS.MIL.XPND.GD.ZS	NaN	NaN	NaN	NaN	NaN	NaN	...	1.878156	2.067426	1.896713	1.821927	1.838564	1.872334	1.915341	1.934922	1.922962	NaN

1 rows × 62 columns

chn = data.loc[(data['Indicator Name']=='Military expenditure (% of GDP)') & \
               (data['Country Code']=='CHN'), :].drop(data.columns[range(3)], axis=1)
chn.head()

	Indicator Code	1960	1961	1962	1963	1964	1965	1966	1967	1968	...	2008	2009	2010	2011	2012	2013	2014	2015	2016	Unnamed: 61
134507	MS.MIL.XPND.GD.ZS	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	...	1.878156	2.067426	1.896713	1.821927	1.838564	1.872334	1.915341	1.934922	1.922962	NaN

1 rows × 59 columns

chn = pd.Series(data=chn.values[0], index=chn.columns)
chn.dropna(inplace=True)
chn.head()

Indicator Code    MS.MIL.XPND.GD.ZS
1989                       2.499185
1990                       2.555996
1991                       2.407892
1992                       2.518629
dtype: object

usa = data.loc[(data['Indicator Name']=='Military expenditure (% of GDP)') & \
               (data['Country Code']=='USA'), :].drop(data.columns[range(3)], axis=1) #USA
usa = pd.Series(data=usa.values[0], index=usa.columns)
usa.dropna(inplace=True)
usa.head()

Indicator Code    MS.MIL.XPND.GD.ZS
1960                        8.35266
1961                       8.487129
1962                       8.656586
1963                       8.189007
dtype: object

ind = data.loc[(data['Indicator Name']=='Military expenditure (% of GDP)') & \
               (data['Country Code']=='IND'), :].drop(data.columns[range(3)], axis=1) #India
ind = pd.Series(data=ind.values[0], index=ind.columns)
ind.dropna(inplace=True)
ind.head()

Indicator Code    MS.MIL.XPND.GD.ZS
1960                       1.866015
1961                       1.933365
1962                       2.561202
1963                       3.758057
dtype: object

gbr = data.loc[(data['Indicator Name']=='Military expenditure (% of GDP)') & \
               (data['Country Code']=='GBR'), :].drop(data.columns[range(3)], axis=1) #United Kingdom
gbr = pd.Series(data=gbr.values[0], index=gbr.columns)
gbr.dropna(inplace=True)
gbr.head()

Indicator Code    MS.MIL.XPND.GD.ZS
1960                       6.343041
1961                       6.190022
1962                       6.210394
1963                       6.082126
dtype: object

n_years = chn.shape[0]
print("#Years: ", n_years+1)

#Years:  30

plt.figure(figsize=(5.5, 5.5))
usa[n_years+1:2*n_years].plot(linestyle='-', marker='*', color='b')
chn[1:n_years].plot(linestyle='-', marker='*', color='r')
gbr[n_years+1:2*n_years].plot(linestyle='-', marker='*', color='g')
ind[n_years+1:2*n_years].plot(linestyle='-', marker='*', color='y')
plt.legend(['USA','CHINA','UK','INDIA'], loc=1)
plt.title('Miltitary expenditure of 4 countries over 30 years')
plt.ylabel('Military expenditure (% of GDP)')
plt.xlabel('Years');

1.5. Estructuras internas de las series temporales

• En esta sección, explicaremos conceptualmente las siguientes características especiales de los datos de series temporales que requieren un tratamiento matemático especial

  • Tendencia general

  • Estacionalidad

  • Movimientos cíclicos

  • Componentes irregulares

Observación

• La mayoría de las series temporales presentan una o varias de las estructuras internas mencionadas. Basándose en esta noción, una serie temporal puede expresarse como

  \[ y_{t}=F_{t}+S_{t}+C_{t}+\varepsilon_{t}, \]

  que es una suma de los componentes de tendencia, componentes estacionales, cíclicas e irregulares en ese orden. Aquí, \(t\) es el índice temporal en el que observaciones sobre la serie se han tomado en \(t = 1,2,3, \dots, T\) puntos sucesivos e igualmente espaciados en el tiempo.

• El objetivo del análisis de series temporales es descomponer una serie temporal en sus características constitutivas y desarrollar modelos matemáticos para ellas. Estos modelos se utilizan para comprender las causas del comportamiento observado de la serie temporal y predecirla para momentos futuros.

1.6. Tendencia general

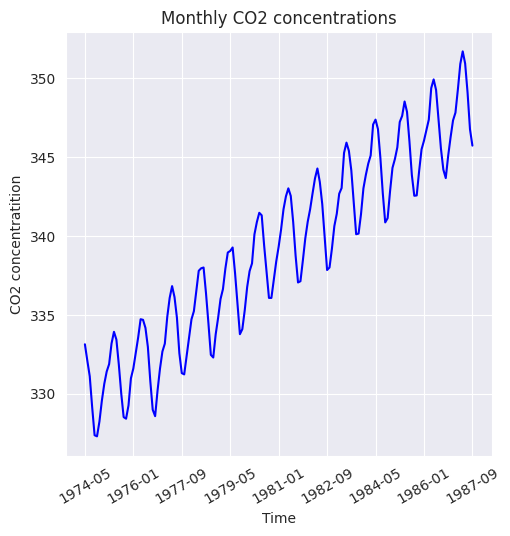
• Cuando una serie temporal presenta un movimiento ascendente o descendente a largo plazo, se dice que tiene tendencia general. Una forma rápida de comprobar la presencia de una tendencia general es trazar la serie temporal como en la siguiente figura, que muestra las concentraciones de CO2 en el aire medidas durante 1974 hasta 1987

import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns

data = pd.read_excel('/home/lihkir/Data/Monthly_CO2_Concentrations.xlsx', converters={'Year': np.int32, 'Month': np.int32})

data.head()

	CO2	Year	Month
0	333.13	1974	5
1	332.09	1974	6
2	331.10	1974	7
3	329.14	1974	8
4	327.36	1974	9

• Creamos índice de filas del DataFrame utilizando las columnas Year y Month

data.index = data['Year'].astype(str) + '-' + data['Month'].astype(str).map(lambda x: '0'+x if len(x) == 1 else x)
data.head()

	CO2	Year	Month
1974-05	333.13	1974	5
1974-06	332.09	1974	6
1974-07	331.10	1974	7
1974-08	329.14	1974	8
1974-09	327.36	1974	9

data = data.loc[(~pd.isnull(data['CO2'])) & \
                (~pd.isnull(data['Year']))& \
                (~pd.isnull(data['Month']))]

data.sort_values(['Year', 'Month'], inplace=True)

plt.figure(figsize=(5.5, 5.5))
data['CO2'].plot(color='b')
plt.title('Monthly CO2 concentrations')
plt.xlabel('Time')
plt.ylabel('CO2 concentratition')
plt.xticks(rotation=30);

• Nótese que, pd.infer_freq() devuelve "MS", lo cual significa que la serie de tiempo tiene una frecuencia mensual y que cada punto de datos representa el primer día de cada mes

data.index = pd.to_datetime(data.index, format='%Y-%m')
frecuencia = pd.infer_freq(data.index)
print("Frecuencia: ", frecuencia)

Frecuencia:  MS

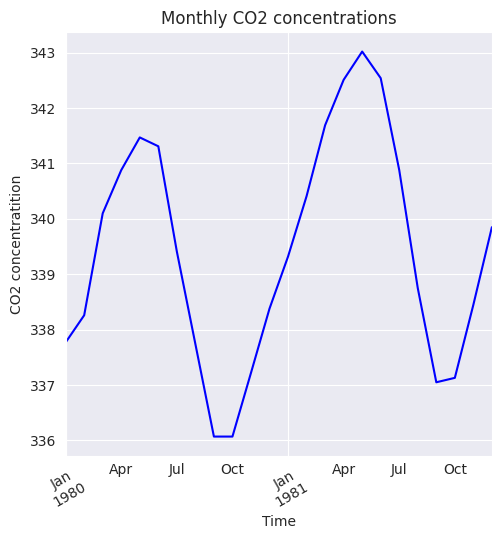
• Sin embargo, la tendencia general puede no ser evidente a corto plazo. Los efectos a corto plazo como las fluctuaciones estacionales y las variaciones irregulares hacen que las series temporales vuelvan a registrar valores más bajos o más altos observados en el pasado, por lo que pueden ocultar temporalmente cualquier tendencia general.

• Esto es evidente en la misma serie temporal de concentraciones de CO2 cuando se considera de 1979 a 1981, como se muestra en la siguiente figura. Por tanto, para revelar la tendencia general, necesitamos una serie temporal que se remonte sustancialmente al pasado.

plt.figure(figsize=(5.5, 5.5))
data['CO2'].loc[(data['Year']==1980) | (data['Year']==1981)].plot(color='b')
plt.title('Monthly CO2 concentrations')
plt.xlabel('Time')
plt.ylabel('CO2 concentratition')
plt.xticks(rotation=30);

Observación

• La tendencia general de la serie temporal se debe a cambios fundamentales o sistémicos del proceso o sistema que representa. Por ejemplo, el movimiento ascendente de las concentraciones de CO2 entre 1974 y 1987 puede atribuirse al aumento gradual de los automóviles y la industrialización durante esos años.

• La tendencia de una serie temporal se modela comúnmente mediante una regresión respecto al tiempo y otras variables conocidas como explicativas. Esta regresión se usa para predecir el movimiento a largo plazo de la serie. Los residuos de esta regresión revelan otras características como la estacionalidad, ciclos y variaciones irregulares.

• A continuación, vamos a ajustar la línea de tendencia. Para ello importamos la clase LinearRegression de scikit-learn y ajustamos un modelo lineal al índice temporal. Para instalar la librería, utilice la orden

pip install -U sklearn-learn

from sklearn.linear_model import LinearRegression
import numpy as np

trend_model = LinearRegression(fit_intercept=True)
trend_model.fit(np.arange(data.shape[0]).reshape((-1,1)), data['CO2'])

LinearRegression()

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

print('Trend model coefficient={} and intercept={}'.format(trend_model.coef_[0], trend_model.intercept_))

Trend model coefficient=0.1209930124223602 and intercept=329.45310559006214

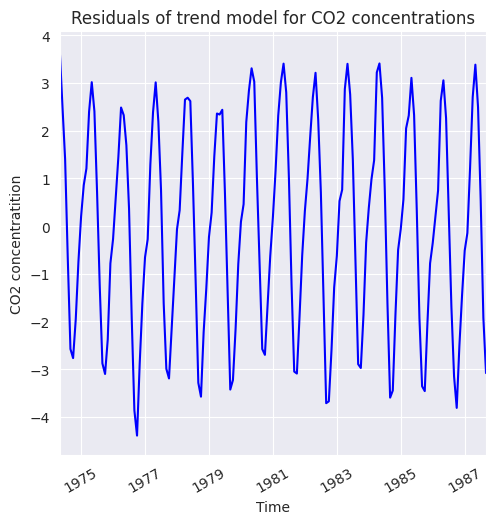
• El residual obtenido a partir del modelo de línea de tendencia se muestra en la siguiente figura, el cual presenta un comportamiento estacional, el cual se analizará en la siguiente sección. Los residuos se calculan y se representan mediante la siguiente línea de código

residuals = np.array(data['CO2']) - trend_model.predict(np.arange(data.shape[0]).reshape((-1,1)))

plt.figure(figsize=(5.5, 5.5))
pd.Series(data=residuals, index=data.index).plot(color='b')
plt.title('Residuals of trend model for CO2 concentrations')
plt.xlabel('Time')
plt.ylabel('CO2 concentratition')
plt.xticks(rotation=30);

1.7. Estacionalidad

Introducción

• La estacionalidad muestra variaciones repetitivas y periódicas en una serie temporal, comúnmente reveladas durante el análisis exploratorio de datos. Por ejemplo, las fluctuaciones mensuales en las emisiones de CO2 o en las ventas de productos estacionales como los regalos navideños evidencian esta estacionalidad.

• Una técnica práctica para determinar la estacionalidad es el análisis exploratorio de datos mediante los siguientes gráficos:

  • Gráfico de secuencia de series

  • Gráfico de subseries estacionales

  • Gráficos de cajas múltiples

1.8. Gráfico de secuencia de series

• Un simple gráfico de secuencia de ejecución de la serie temporal original con el tiempo en el eje \(x\) y la variable en el eje \(y\) sirve para indicar las siguientes propiedades de la serie temporal:

  • Movimientos en la media de la serie

  • Cambios en la varianza

  • Presencia de valores atípicos

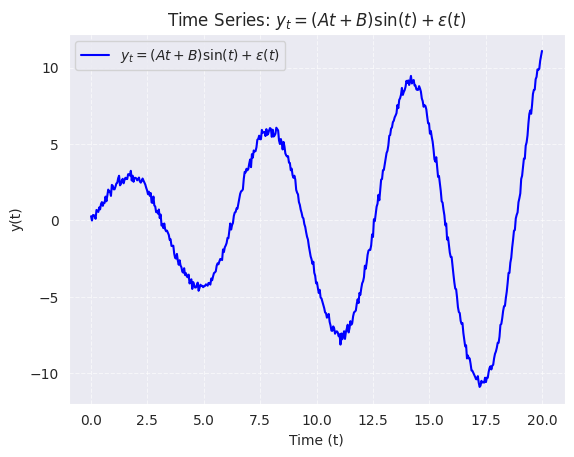
• Por ejemplo, el gráfico de la secuencia de ejecución de una serie temporal hipotética que se obtiene a partir de la formulación matemática

  \[ y_{t} = (At + B)\sin(t) + \varepsilon(t) \]

  con una media dependiente del tiempo y error \(\varepsilon(t)\) que varía como una distribución normal \(N(0, At + b)\).

• En casos como este, un gráfico de secuencia de ejecución es una forma eficaz de identificar el desplazamiento de la media y la varianza de la serie, así como los valores atípicos. El gráfico de la serie temporal sin tendencia es un ejemplo de gráfico de secuencia.

import numpy as np
import matplotlib.pyplot as plt

A = 0.5 
B = 2.0 
t = np.linspace(0, 20, 500)  
epsilon = np.random.normal(0, 0.2, len(t))

y_t = (A * t + B) * np.sin(t) + epsilon

plt.figure()
plt.plot(t, y_t, label=r'$y_{t} = (At + B)\sin(t) + \varepsilon(t)$', color='blue')
plt.title("Time Series: $y_{t} = (At + B)\\sin(t) + \\varepsilon(t)$")
plt.xlabel("Time (t)")
plt.ylabel("y(t)")
plt.grid(True, linestyle='--', alpha=0.6)
plt.legend()
plt.show()

1.9. Gráfico de subserie estacional

Subseries estacionales

• Para una periodicidad conocida de variaciones estacionales, las subseries estacionales vuelven a dibujar la serie original en lotes de períodos sucesivos. Por ejemplo, la periodicidad de las concentraciones de CO2 es de 12 meses y, basándose en ella, se traza una subserie estacional de la media y la desviación estándar de los residuos.

• Para visualizar estacionalidad en los residuos, creamos medias y desviaciones estándar trimestrales. Una subserie estacional revela dos propiedades:

  • Variaciones dentro de las estaciones como dentro de un lote de meses sucesivos.

  • Variaciones entre las estaciones como entre lotes de meses sucesivos

• En primer lugar, tenemos que añadir los residuos y las etiquetas trimestrales al DataFrame de concentraciones de CO2 de la siguiente forma

data.head()

	CO2	Year	Month
1974-05-01	333.13	1974	5
1974-06-01	332.09	1974	6
1974-07-01	331.10	1974	7
1974-08-01	329.14	1974	8
1974-09-01	327.36	1974	9

data['Residuals'] = residuals
month_quarter_map = {1: 'Q1', 2: 'Q1', 3: 'Q1',
                     4: 'Q2', 5: 'Q2', 6: 'Q2',
                     7: 'Q3', 8: 'Q3', 9: 'Q3',
                     10: 'Q4', 11: 'Q4', 12: 'Q4'}
data['Quarter'] = data['Month'].map(lambda m: month_quarter_map.get(m))

• A continuación, se calculan la media estacional y las desviaciones típicas, agrupando los datos por Year y Quarter. Esto crea el nuevo DataFrame como seasonal_sub_series_data, que tiene la media trimestral y las desviaciones estándar a lo largo de los años. Estas columnas se renombran como sigue:

seasonal_sub_series_data = data.groupby(by=['Year', 'Quarter'])['Residuals'].aggregate([np.mean, np.std])
seasonal_sub_series_data.columns = ['Quarterly Mean', 'Quarterly Standard Deviation']

• Creamos índices de filas de seasonal_sub_series_data utilizando Year & Quarter

seasonal_sub_series_data.reset_index(inplace=True)
seasonal_sub_series_data.index = seasonal_sub_series_data['Year'].astype(str) + '-' + seasonal_sub_series_data['Quarter']
seasonal_sub_series_data.head()

	Year	Quarter	Quarterly Mean	Quarterly Standard Deviation
1974-Q2	1974	Q2	3.096398	0.820946
1974-Q3	1974	Q3	-0.616085	1.991671
1974-Q4	1974	Q4	-1.822397	1.014952
1975-Q1	1975	Q1	0.754624	0.511890
1975-Q2	1975	Q2	2.604978	0.355093

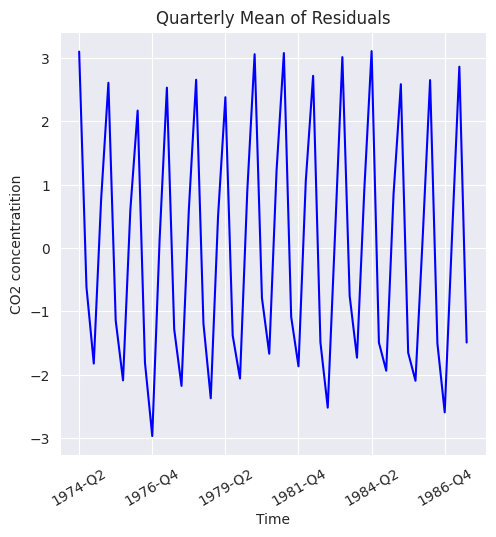
plt.figure(figsize=(5.5, 5.5))
seasonal_sub_series_data['Quarterly Mean'].plot(color='b')
plt.title('Quarterly Mean of Residuals')
plt.xlabel('Time')
plt.ylabel('CO2 concentratition')
plt.xticks(rotation=30);

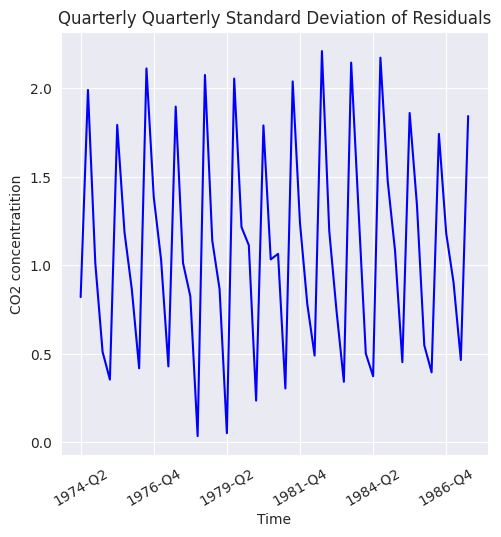
plt.figure(figsize=(5.5, 5.5))
seasonal_sub_series_data['Quarterly Standard Deviation'].plot(color='b')
plt.title('Quarterly Quarterly Standard Deviation of Residuals')
plt.xlabel('Time')
plt.ylabel('CO2 concentratition')
plt.xticks(rotation=30);

• Nótese que, el agrupamiento por año y trimestre (Year, Quarter) y el cálculo de la media trimestral indica que hay variaciones regulares en los datos residuales según el trimestre. Esto confirma la presencia de patrones estacionales periódicos.

• La desviación estándar trimestral muestra que la magnitud de las fluctuaciones también tiene un comportamiento estacional. En algunos trimestres, los datos pueden ser más variables que en otros. Esto sugiere heterocedasticidad estacional.

1.10. Gráficos de cajas múltiples

Boxplot

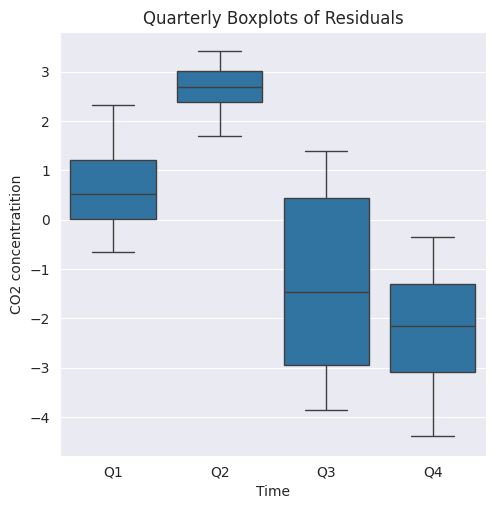
• El gráfico de la subserie estacional para la serie de residuos de LinearRegression puede ser más informativo si se redibuja con gráficos de caja estacionales como se muestra en la siguiente figura.

• Un gráfico de cajas muestra tanto la tendencia central como la dispersión de los datos estacionales en un lote de unidades temporales. Además, la separación entre dos gráficos de caja adyacentes revela las variaciones dentro de la temporada

plt.figure(figsize=(5.5, 5.5))
g = sns.boxplot(data=data[data['Year'] > 1974], y='Residuals', x='Quarter')
g.set_title('Quarterly Boxplots of Residuals')
g.set_xlabel('Time')
g.set_ylabel('CO2 concentratition');

Observación

• Q1 y Q2 tienen medianas positivas, lo que indica que los residuos en estos trimestres tienden a ser positivos, lo cual podría sugerir una subestimación sistemática del modelo en estas épocas del año. Q3 y Q4 tienen medianas negativas, lo que sugiere una sobreestimación sistemática en estos trimestres.

• Q2 muestra la menor dispersión, lo que indica una menor variabilidad de los residuos durante este trimestre. Esto podría reflejar una mayor estabilidad en las predicciones del modelo en este período. Q3 tiene la mayor dispersión, lo que sugiere mayor variabilidad o incertidumbre en las predicciones del modelo en este trimestre.

1.11. Cambios cíclicos

Cambios cíclicos

• Los cambios cíclicos son movimientos que se observan cada pocas unidades de tiempo, menos frecuentes que las fluctuaciones estacionales, pueden no tener un período fijo y suelen ocurrir cada pocos años. Se necesitan datos a largo plazo para identificarlos, como los ciclos económicos recurrentes.

• La inflación del CPI en India y Estados Unidos (consumer price index (CPI)) muestra patrones cíclicos cada 2-2.5 años. Los datos se obtuvieron de datamarket.

inflation = pd.read_excel('/home/lihkir/Data/inflation-consumer-prices-annual.xlsx', parse_dates=['Year'])

inflation.head()

	Year	India	United States
0	1960-01-01	1.783265	1.509929
1	1961-01-01	1.752022	1.075182
2	1962-01-01	3.576159	1.116071
3	1963-01-01	2.941176	1.214128
4	1964-01-01	13.354037	1.308615

plt.figure(figsize=(5.5, 5.5))
plt.plot(range(1960,2017), inflation['India'], linestyle='-', marker='*', color='r')
plt.plot(range(1960,2017), inflation['United States'], linestyle='-', marker='.', color='b')
plt.legend(['India','United States'], loc=2)
plt.title('Inflation in Consumer Price Index')
plt.ylabel('Inflation')
plt.xlabel('Years');

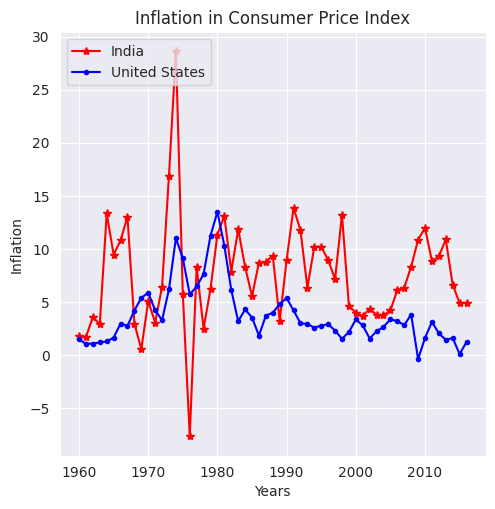
• La figura anterior muestra un cambio cíclico entre 1970 y 1980. La alta inflación en Estados Unidos e India entre 1970 y 1980 se debió principalmente a los aumentos en los precios del petróleo a nivel mundial, políticas económicas expansivas y presión sobre los precios por aumento de la demanda debido al rápido crecimiento económico.

1.12. Componentes irregulares

Variaciones irregulares

• A pesar de que nuestro modelo que incluye cuatro componentes para expresar una serie temporal, aún puede haber un componente irregular. Este componente es un error irreducible que es aleatorio y no muestra una relación sistemática con el tiempo.

• Refleja variaciones inesperadas en la serie temporal que son estocásticas y no pueden predecirse definitivamente con un modelo matemático, debido a la falta de información sobre variables explicativas o la presencia de ruido aleatorio.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.seasonal import seasonal_decompose

np.random.seed(42)
n = 100
time = np.arange(n)

trend = 0.1 * time  
seasonality = 5 * np.sin(2 * np.pi * time / 12)  
irregular = np.random.normal(0, 2, n)

series = trend + seasonality + irregular

date_range = pd.date_range(start="2023-01-01", periods=n, freq='M')
data = pd.DataFrame({'Date': date_range, 'Value': series}).set_index('Date')

decomposition = seasonal_decompose(data['Value'], model='additive', period=12)

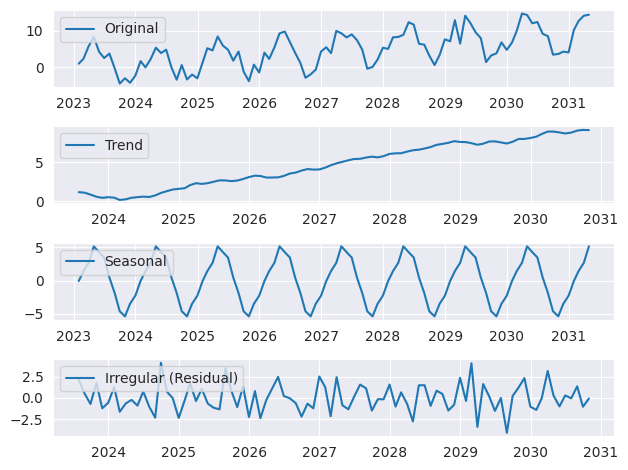
plt.figure()
plt.subplot(411)
plt.plot(data['Value'], label='Original')
plt.legend(loc='upper left')
plt.subplot(412)
plt.plot(decomposition.trend, label='Trend')
plt.legend(loc='upper left')
plt.subplot(413)
plt.plot(decomposition.seasonal, label='Seasonal')
plt.legend(loc='upper left')
plt.subplot(414)
plt.plot(decomposition.resid, label='Irregular (Residual)')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()

1.13. Modelos de análisis de series temporales

Introducción

• El objetivo del análisis de series temporales es desarrollar un modelo matemático que pueda explicar el comportamiento observado de una serie temporal y, posiblemente, predecir su estado futuro.

• El modelo elegido debe ser capaz de dar cuenta de una o más de las estructuras internas que pueden estar presentes. Con este fin, daremos una visión general de los siguientes modelos que se utilizan a menudo como componentes básicos del análisis de series temporales:

  • Modelos de media cero

  • Recorrido aleatorio

  • Modelos de tendencia

  • Modelos de estacionalidad

1.14. Modelos de media cero

Definición

• Los modelos de media cero tienen una media y una varianza constantes y no muestran tendencias predecibles ni estacionalidad. Se supone que las observaciones de un modelo de media cero son independientes e idénticamente distribuidas (iid) y representan el ruido aleatorio en torno a una media fija, que se ha deducido de la serie temporal como un término constante.

• Consideremos que \(Y_{1}, Y_{2},\dots, Y_{T}\) representan las variables aleatorias correspondientes a \(T\) observaciones de un modelo de media cero. Si \(y_{1}, y_{2},\dots, y_{T}\) son \(t\) observaciones de la serie temporal de media cero, la distribución conjunta de las observaciones viene dada por el producto de las funciones de masa de probabilidad para cada índice temporal

\[ P(Y_{1}=y_{1}, Y_{2}=y_{2}, \dots, Y_{T}=y_{T})=f(Y_{1}=y_{1})f(Y_{2}=y_{2})\cdots f(Y_{T}=y_{T}) \]

• Lo más habitual es modelar \(f(Y_{t} = y_{t})\) mediante una distribución normal de media cero y varianza \(\sigma^2\), que se supone que es el error irreducible del modelo y, por tanto, se trata como un ruido aleatorio. La siguiente figura muestra una serie de ruido aleatorio con media cero y distribución normal de varianza unitaria

import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns

np.random.seed(42)
zero_mean_series = np.random.normal(loc=0.0, scale=1., size=100)

plt.figure(figsize=(5.5, 5.5))
g = sns.lineplot(zero_mean_series)
g.set_title('Zero mean model')
g.set_xlabel('Time index');

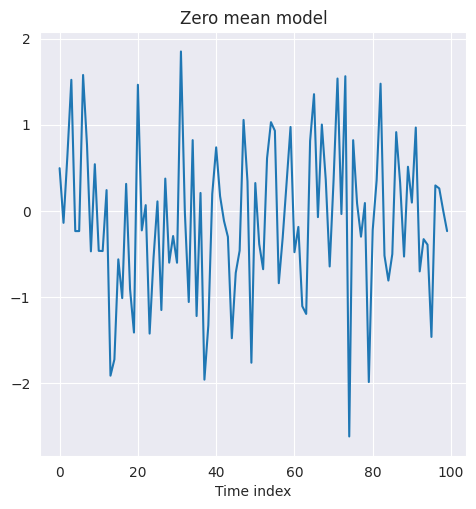
• La media cero con varianza constante representa un ruido aleatorio que puede asumir infinitos posibles valores reales y es adecuado para representar variaciones irregulares en la serie temporal de una variable continua.

• Sin embargo, en muchos casos, el estado observable del sistema o proceso puede ser de naturaleza discreta y limitarse a un número finito de valores posibles \(s_{1}, s_{2}, \dots, s_{m}\). En tales casos, se supone que la variable observada \(X\) obedece a la distribución multinomial,

  \[ P(X = s_{1}) = p_{1}, P(X = s_{2}) = p_{2}, \dots, P(X = s_{m}) = p_{m}~\text{tal que}~p_{1} + p_{2} + \cdots + p_{m} = 1. \]

  Una serie temporal de este tipo es un proceso estocástico discreto.

• El lanzamiento múltiple de un dado a lo largo del tiempo es un ejemplo de proceso estocástico discreto con seis resultados posibles para cada lanzamiento. Un proceso estocástico discreto más sencillo es un proceso binario como lanzar una moneda con solo dos resultados: cara y sello.

1.15. Camino aleatorio

Definición

• Un paseo aleatorio viene dado como una suma de \(n\) iids, que tiene media cero y varianza constante. A partir de esta definición, la realización de un paseo aleatorio en el índice de tiempo \(t\) viene dada por la suma

  \[ S = y_{1} + y_{2} + \cdots + y_{T}. \]

• La siguiente figura muestra el paseo aleatorio obtenido a partir de las iids, que varían según una distribución normal de media cero y varianza unitaria.

• El paseo aleatorio es importante porque si se encuentra un comportamiento de este tipo en una serie temporal, se puede fácilmente reducir a un modelo de media cero tomando las diferencias de las observaciones de dos índices temporales consecutivos como

  \[ S_{t}-S_{t-1} = y_{t} \]

  obteniendo así una serie iid con media cero y varianza constante.

• El paseo aleatorio puede generarse tomando la suma acumulada del modelo de media cero discutido en la sección anterior. El siguiente código lo implementa

random_walk = np.cumsum(zero_mean_series)

plt.figure(figsize=(5.5, 5.5))
g = sns.lineplot(random_walk)
g.set_title('Random Walk')
g.set_xlabel('Time index');

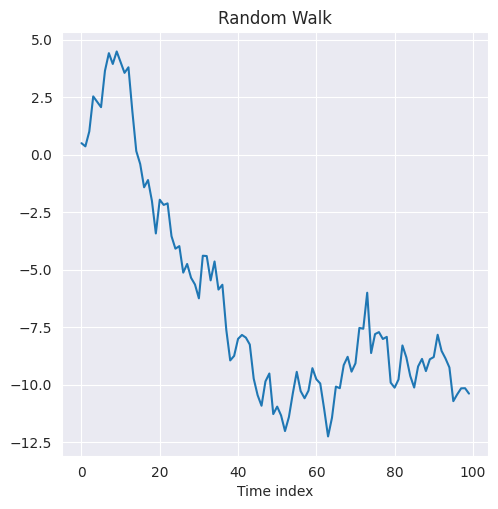
• El código dado genera y visualiza un paseo aleatorio (random walk) a partir de una serie de tiempo con media cero (zero_mean_series). A continuación, se describen los pasos detallados: np.cumsum(zero_mean_series):

  • Calcula la suma acumulada de los valores en zero_mean_series.

  • Esta operación transforma la serie original en un paseo aleatorio, donde cada nuevo valor es la suma del anterior más un incremento aleatorio.

  • Matemáticamente, esto se expresa como:

    \[ X_t = X_{t-1} + \epsilon_t, \]

    donde \(\epsilon_t\) representa los valores de zero_mean_series.

1.16. Modelos de tendencia

Introducción

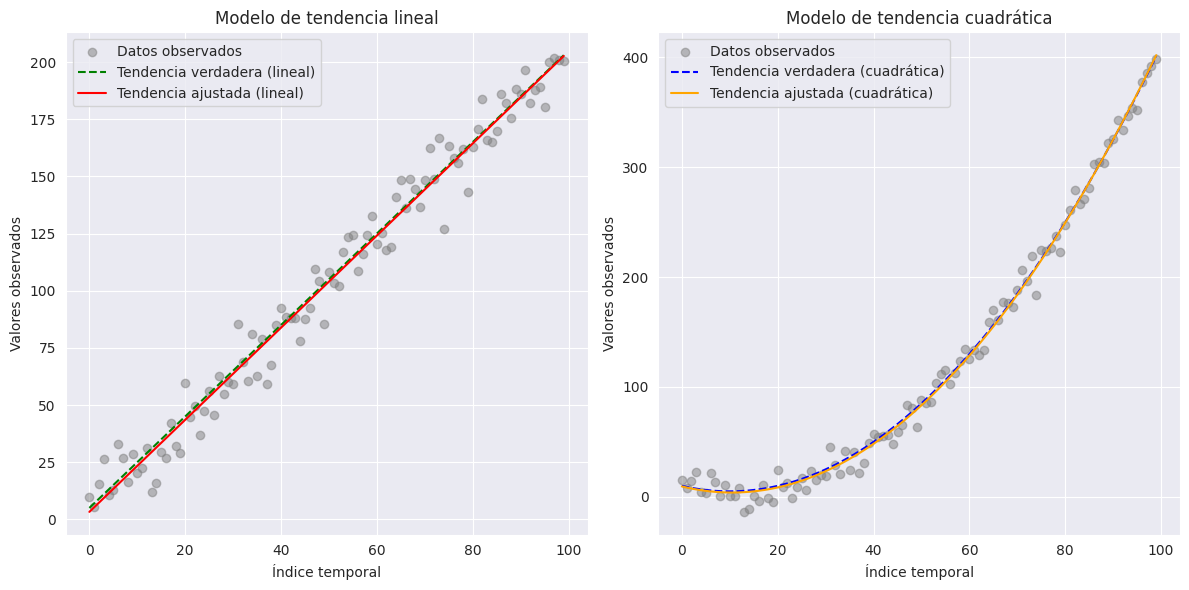
• Este tipo de modelo pretende captar la tendencia a largo plazo de la serie temporal que puede ajustarse como regresión lineal del índice temporal. Cuando la serie temporal no presenta fluctuaciones periódicas o estacionales, puede expresarse simplemente como la suma de la tendencia y la media nula como

  \[ y_{t} = \mu(t) + \varepsilon_{t} \]

  donde \(\mu(t)\) es la tendencia a largo plazo dependiente del tiempo de la serie.

• La elección del modelo de tendencia \(\mu(t)\) es fundamental para captar correctamente el comportamiento de la serie temporal. El análisis exploratorio de datos suele proporcionar pistas para plantear la hipótesis de si el modelo debería ser lineal o no lineal en \(t\).

• Un modelo lineal es simplemente \(\mu(t) = wt + b\), mientras que un modelo cuadrático es \(\mu(t) = w_{1}t + w_{2}t^{2} + b\). A veces, la tendencia se puede hipotetizar mediante una relación compleja en términos del índice temporal, como \(\mu(t) = w_{0}t^{p} + b\) o \(\mu(t)=w_{0}e^{w_{1}t}\).

• Los pesos y sesgos en los modos de tendencia como los discutidos anteriormente se obtienen ejecutando una regresión con \(t\) como variable explicativa y \(\mu(t)\) como respuesta. Los residuos \(y_{t} - \mu(t)\) del modelo de tendencia es considerado el ruido irreducible y como realización del componente de media cero \(\varepsilon_{t}\).

import numpy as np
import matplotlib.pyplot as plt


np.random.seed(42)
t = np.arange(0, 100, 1)  
true_trend_linear = 2 * t + 5  # Modelo de tendencia lineal: µ(t) = 2t + 5
true_trend_quadratic = 0.05 * t**2 - t + 10  # Modelo cuadrático: µ(t) = 0.05t^2 - t + 10

noise = np.random.normal(0, 10, size=len(t))
y_linear = true_trend_linear + noise  # Serie con tendencia lineal
y_quadratic = true_trend_quadratic + noise  # Serie con tendencia cuadrática

# Modelo lineal: y = wt + b
coeffs_linear = np.polyfit(t, y_linear, 1)  # Grado 1
fitted_trend_linear = np.polyval(coeffs_linear, t)

# Modelo cuadrático: y = w1t + w2t^2 + b
coeffs_quadratic = np.polyfit(t, y_quadratic, 2)  # Grado 2
fitted_trend_quadratic = np.polyval(coeffs_quadratic, t)

plt.figure(figsize=(12, 6))

plt.subplot(1, 2, 1)
plt.scatter(t, y_linear, color='gray', alpha=0.5, label='Datos observados')
plt.plot(t, true_trend_linear, color='green', label='Tendencia verdadera (lineal)', linestyle='dashed')
plt.plot(t, fitted_trend_linear, color='red', label='Tendencia ajustada (lineal)')
plt.title('Modelo de tendencia lineal')
plt.xlabel('Índice temporal')
plt.ylabel('Valores observados')
plt.legend()

plt.subplot(1, 2, 2)
plt.scatter(t, y_quadratic, color='gray', alpha=0.5, label='Datos observados')
plt.plot(t, true_trend_quadratic, color='blue', label='Tendencia verdadera (cuadrática)', linestyle='dashed')
plt.plot(t, fitted_trend_quadratic, color='orange', label='Tendencia ajustada (cuadrática)')
plt.title('Modelo de tendencia cuadrática')
plt.xlabel('Índice temporal')
plt.ylabel('Valores observados')
plt.legend()

plt.tight_layout()
plt.show()

1.17. Modelos de estacionalidad

Definición

• La estacionalidad se manifiesta como fluctuaciones periódicas y repetitivas en una serie temporal y, por tanto, se modelan como una suma ponderada de ondas senoidales de periodicidad conocida.

• Suponiendo que la tendencia a largo plazo se ha eliminado mediante una línea de tendencia, el modelo de estacionalidad puede expresarse como \(y_{t} = S_{t}+ \varepsilon_{t}\), donde la variación estacional es

  \[ S_{t}=\sum_{k=1}^{L}(w_{k}\cos(\alpha t)+v_{k}\sin(\alpha t))+b, \]

  con periocidad \(\alpha\).

• Los modelos de estacionalidad también se conocen como modelos de regresión armónica, ya que intentan ajustar la suma de múltiples ondas senoidales. Los cuatro modelos descritos aquí son los componentes básicos de un modelo de series temporales completo.

Observación

• Como ya se habrá dado cuenta, un modelo de suma cero representa el error irreducible del sistema y los otros tres modelos pretenden transformar una serie temporal dada en modelos de suma cero mediante transformaciones matemáticas adecuadas. Para obtener previsiones en series temporales originales, se aplican las transformaciones inversas pertinentes.

• En las próximas secciones se detallarán los cuatro modelos aquí analizados. Sin embargo, hemos llegado a un punto en el que podemos resumir el enfoque genérico de un análisis de series temporales en los siguientes cuatro pasos:

  • Visualizar los datos en distintas etapas del índice temporal para revelar las tendencias a largo plazo y las fluctuaciones estacionales.

  • Ajustar la línea de tendencia para captar tendencias a largo plazo y trazar los residuos para comprobar si hay estacionalidad o error irreducible

  • Ajustar de un modelo de regresión armónica para captar la estacionalidad

  • Trazar los residuos dejados por el modelo de estacionalidad para comprobar si hay error irreducible.

• Estos pasos suelen bastar para desarrollar modelos matemáticos para la mayoría de las series temporales. Los modelos individuales de tendencia y estacionalidad pueden ser sencillos o complejos, dependiendo de la serie temporal original y de la aplicación.

1.18. Autocorrelación y autocorrelación parcial

Introducción

• Tras aplicar las transformaciones matemáticas comentadas en el apartado anterior, a menudo nos encontramos con lo que se conoce como una serie temporal estacionaria (o débilmente estacionaria), que se caracteriza por una media constante \(\text{E}(y_{t})\) y una correlación que solo depende del desfase entre dos pasos temporales, pero independiente del valor del paso temporal, esto es, su distribución de probabilidad es completamente independiente del tiempo.

• Este tipo de covarianza es la clave en el análisis de series temporales y se denomina autocovarianza o autocorrelación, cuando se normaliza en el intervalo de -1 a 1. La autocorrelación refleja el grado de dependencia lineal entre la serie temporal en el índice \(t\) y las series temporales de los índices \(t-k\) o \(t+k\).

• Una autocorrelación positiva indica que los valores presentes y futuros de la serie temporal se mueven en la misma dirección, mientras que los valores negativos significan que los valores presentes y futuros se mueven en sentido contrario.

• Si la autocorrelación es cercana a cero, las dependencias temporales dentro de la serie pueden ser difíciles de encontrar. Debido a esta propiedad, la autocorrelación es útil para predecir el estado futuro de una serie temporal a \(h\) pasos por delante.

Definición

• La covarianza entre \(y_{t}\) y su valor en otro período de tiempo, digamos, \(y_{t+k}\) se denomina autocovarianza en el desfase (lag) \(k\) y se define como

\[ \gamma_{k}=\textsf{Cov}(y_{t}, y_{t+k})=\textsf{E}[(y_{t}-\mu)(y_{t+k}-\mu)]. \]

• La colección de los valores de \(\gamma_{k}, k = 0, 1, 2,\dots\) se denomina función de autocovarianza. Tenga en cuenta que la autocovarianza en el lag \(k = 0\) es solo la varianza de la serie temporal; es decir, \(\gamma_{0}=\sigma_{y}^{2}\), que es constante para una serie de tiempo estacionaria.

• El coeficiente de autocorrelación en el lag \(k\) para una serie temporal estacionaria es

\[ \rho_{k}=\frac{\textsf{E}[(y_{t}-\mu)(y_{t+k}-\mu)]}{\sqrt{\textsf{E}[(y_{t}-\mu)^2]\textsf{E}[(y_{t+k}-\mu)^{2}]}}=\frac{\textsf{Cov}(y_{t}, y_{t+k})}{\textsf{Var}(y_{t})}=\frac{\gamma_{k}}{\gamma_{0}}. \]

• El conjunto de los valores de \(\rho_{k}, k = 0, 1, 2, \dots\) se denomina función de autocorrelación (ACF). Obsérvese que, por definición, \(\rho_{0} = 1\). Además, la ACF es independiente de la escala de medición de la serie temporal, por lo que es una cantidad adimensional. Adicionalmente, \(\rho_{k} = \rho_{-k}\); es decir, la ACF es simétrica en torno a cero, por lo que solo es necesario calcular la mitad positiva (o negativa).

• Es necesario estimar la autocovarianza y los ACF a partir de una serie temporal de longitud finita, digamos, \(y_{1}, y_{2}, \dots, y_{T}\). La estimación habitual de la función de autocovarianza es

  \[\begin{split} \\[1mm] c_{k}=\hat{\gamma}_{k}=\frac{1}{T}\sum_{t=1}^{T-k}(y_{t}-\overline{y})(y_{t+k}-\overline{y}),\quad k=1,2,\dots,K, \end{split}\]

  y la ACF es estimada por la función de autocorrelación muestral (o ACF muestral)

  \[\begin{split} \\[1mm] r_{k}=\hat{\rho}_{k}=\frac{c_{k}}{c_{0}},\quad k=0,1,2,\dots,K. \end{split}\]

• El siguiente tutorial puede ser de utilidad para quienes gozan usar Excel. En esta oportunidad puede ser usado como calculadora para obtener de forma manual la función ACF (ver How to calculate ACF by 2 ways in Excel)

Observación

• Una buena regla general es que se necesitan al menos 50 observaciones para obtener una estimación fiable de la ACF, y las autocorrelaciones de las muestras individuales deben calcularse hasta el retardo \(K\), donde \(K\) es aproximadamente \(T/4\).

• A menudo tendremos que determinar si el coeficiente de autocorrelación en un determinado retardo es cero. Esto puede hacerse comparando el coeficiente de autocorrelación de la muestra en el retardo \(k, r_{k}\), con su error estándar.

• Sí, suponemos que las observaciones no están correlacionadas, es decir, \(\rho_{k} = 0\) para todo \(k\), entonces la varianza del coeficiente de autocorrelación de la muestra es (ver [Bartlett, 1946])

  \[\begin{split} \\[1mm] \textsf{Var}(r_{k})\cong\frac{1}{T}, \end{split}\]

  y error estándar es

  \[ \textsf{se}(r_{k})\cong\frac{1}{\sqrt{T}}. \]

• Para abordar el cálculo de este error, Bartlett considera el proceso estocástico discreto AR \(y_{t+1}=\phi y_{t}+\varepsilon_{t+1}\). Para este propósito, utiliza la siguiente expresión para la varianza aproximada del coeficiente de autocorrelación estimado de un proceso normal estacionario dada por

(1.1)\[ \textsf{Var}(r_{k})\cong\frac{1}{T}\sum_{v=-\infty}^{\infty}(\rho_{v}^{2}+\rho_{v+k}\rho_{v-k}-4\rho_{k}\rho_{v}\rho_{v-k}+2\rho_{v}^{2}\rho_{k}^{2}). \]

• Por ejemplo, si \(\rho_{k}=\phi^{|k|},~(-1<\phi<1)\), es decir, la función de autocorrelación se reduce exponencialmente, entonces la Ecuación (1.1) se convierte en (verifíquelo)

\[ \textsf{Var}(r_{k})\cong\frac{1}{T}\left(1+2\sum_{v=1}^{q}\rho_{v}^{2}\right),\quad k>q. \]

• Bajo el supuesto de que los \(\rho_{k}\) son todos cero más allá de un cierto rezago \(k =q\), el error estándar de gran retardo se aproxima a la desviación estándar de \(r_{k}\) para retardos adecuadamente grandes \((k > q)\). Entonces los errores estándar para las autocorrelaciones estimadas \(r_{k}\) adoptan la forma simple (bonus)

\[ \textsf{se}(r_{k})\approx\frac{1}{\sqrt{T}}. \]

1.19. Experimentos numéricos ACF

• La presencia de autocorrelación puede identificarse trazando los valores observados de la función de autocorrelación (ACF) de una serie temporal determinada. Este gráfico suele denominarse ACF. Ilustremos cómo el trazado de los valores observados de la ACF puede ayudar a detectar la presencia de autocorrelación.

• Para ello, trazaremos primero el valor diario del Dow Jones Industrial Average (DJIA) observado durante enero de 2016 a diciembre de 2016

import pandas as pd
from matplotlib import pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

djia_df = pd.read_excel('/home/lihkir/Data/DJIA_Jan2016_Dec2016.xlsx')

djia_df.index = djia_df['Date']
djia_df.head()

	Date	Open	High	Low	Close	Adj Close	Volume
Date
2016-01-04	2016-01-04	17405.480469	17405.480469	16957.630859	17148.939453	17148.939453	148060000
2016-01-05	2016-01-05	17147.500000	17195.839844	17038.609375	17158.660156	17158.660156	105750000
2016-01-06	2016-01-06	17154.830078	17154.830078	16817.619141	16906.509766	16906.509766	120250000
2016-01-07	2016-01-07	16888.359375	16888.359375	16463.630859	16514.099609	16514.099609	176240000
2016-01-08	2016-01-08	16519.169922	16651.890625	16314.570313	16346.450195	16346.450195	141850000

plt.figure(figsize=(5.5, 5.5))
djia_df['Close'].plot(color='b')
plt.title('Dow Jones Industrial Average between Jan 2016 - Dec 2016')
plt.xlabel('Time')
plt.ylabel('Closing Value');

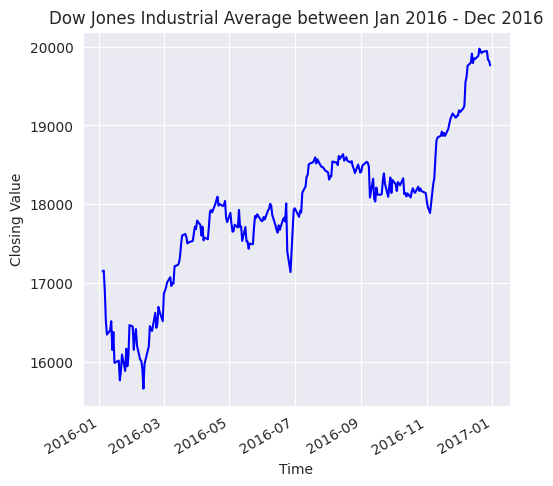
• De la figura anterior se desprende que cuando el DJIA empieza a subir, continúa haciéndolo durante algún tiempo y viceversa. Sin embargo, debemos comprobarlo mediante un gráfico ACF.

• A continuación, se estima la ACF calculando la autocorrelación para diferentes valores del retardo \(h\), que en este caso varía de 0 a 30. La función Pandas.Series.autocorr se utiliza para calcular la autocorrelación para diferentes valores del retardo

lag = range(0,31)
djia_acf = []
for l in lag:
    djia_acf.append(djia_df['Close'].autocorr(l))

• El código anterior, itera sobre una lista de 31 valores de lag, empezando de 0 a 30. Un rezago de 0 índica autocorrelación de una observación consigo misma (\(\text{Cov}(y_{t}, y_{t})/\text{Var}(y_{t})\)) y, por lo tanto, se espera que sea 1.0, como también se confirma en la figura siguiente.

• Autocorrelación en DJIA Close parece disminuir linealmente con el retardo, con un cambio aparente en la tasa de caída en torno a los 18 días. Con un desfase de 30 días, la ACF es ligeramente superior a 0.65.

plt.figure(figsize=(5.5, 5.5))
plt.plot(djia_acf, marker='.', color='b')
plt.title('Autocorrelation function for DJIA')
plt.xlabel('Lag in terms of number of trading days')
plt.ylabel('Autocorrelation function');

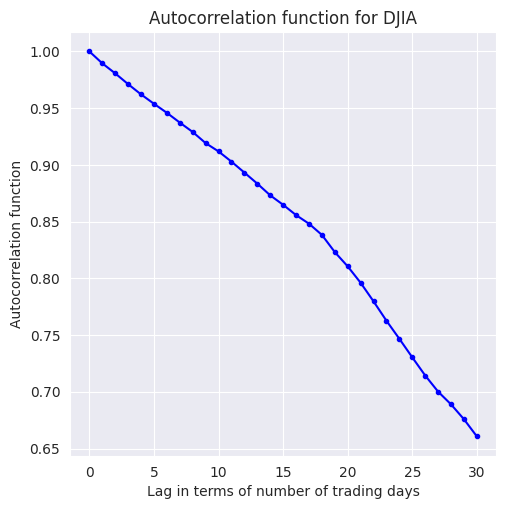
• El gráfico ACF muestra que la autocorrelación, en el caso de los valores de cierre del DJIA, tienen una dependencia funcional del desfase temporal entre las observaciones. Hemos escrito un bucle for para calcular la autocorrelación en distintos retardos y hemos representado los resultados mediante la función sns.pointplot. También se puede utilizar la función plot_acf de statsmodels.graphics.tsaplots para calcular y trazar la autocorrelación en varios rezagos.

• Además, esta función también traza los intervalos de confianza del 95%. La autocorrelación fuera de estos intervalos de confianza es una correlación estadísticamente significativa, mientras que las que están dentro de los intervalos de confianza se deben a ruido aleatorio. La autocorrelación y los intervalos de confianza generados por plot_acf se muestran en la figura siguiente:

plt.figure(figsize=(5.5, 5.5));
plot_acf(djia_df['Close'], lags=31);

<Figure size 550x550 with 0 Axes>

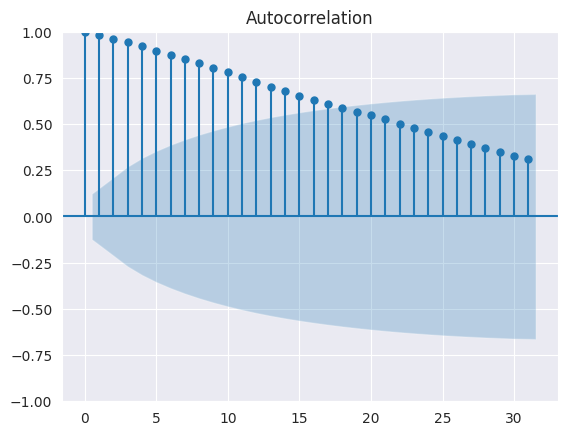
• Hasta ahora hemos hablado de la autocorrelación, que es una medida de la dependencia lineal entre las variables \(y_{t}\) y \(y_{t+k}\). Los modelos autorregresivos (AR) captan esta dependencia como una regresión lineal entre \(y_{t+k}\) y \(y_{t}\). Sin embargo, las series temporales tienden a llevar información y estructuras de dependencia por etapas, por lo que la autocorrelación en el rezago \(k\) también se ve influida por las variables intermedias \(y_t, y_{t+1}, \dots, y_{t+k-1}\). Por lo tanto, la autocorrelación no es la medida correcta de la correlación mutua entre \(y_{t}\) y \(y_{t+k}\) en presencia de las variables intermedias.

• Sería erróneo elegir \(k\) en modelos AR basados en autocorrelación. La autocorrelación parcial (PACF) resuelve este problema midiendo la correlación entre \(y_{t}\) y \(y_{t+k}\) cuando se ha eliminado la influencia de las variables intermedias. Por lo tanto, la autocorrelación parcial en el análisis de series temporales define la correlación entre \(y_{t}\) y \(y_{t+k}\) que no tiene en cuenta los retardos \(t+1, \dots, t+k-1\). La PACF ayuda a identificar el orden \(p\) de un modelo \(AR(p)\). Veamos la autocorrelación parcial de los valores de cierre del DJIA utilizando plot_pacf como sigue

plt.figure(figsize=(5.5, 5.5));
plot_pacf(djia_df['Close'], lags=31);

<Figure size 550x550 with 0 Axes>

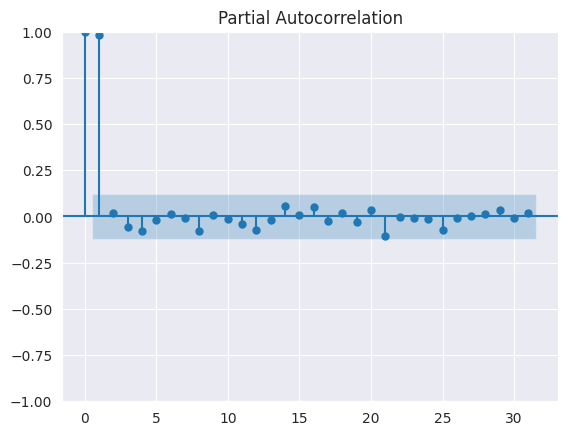
• La primera autocorrelación parcial en el retardo cero es siempre 1.0. Como se observa en el gráfico anterior, la autocorrelación parcial solo en el retardo uno es estadísticamente significativa, mientras que para el resto de los rezagos está dentro de los intervalos de confianza del 95%. Por lo tanto, para los valores de cierre del DJIA el orden de los modelos \(AR\) es uno (usar \(AR(1)\)).

1.20. Análisis de datos de series temporales

Observación

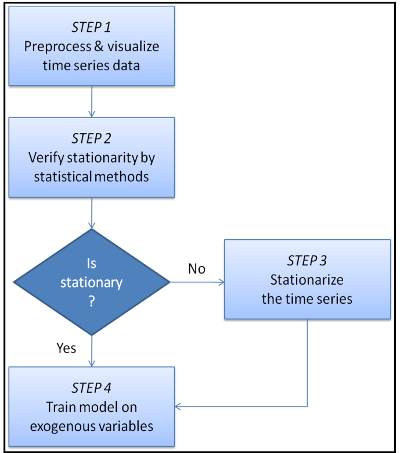
• El análisis de series temporales implica dos pasos clave: visualizar los datos para identificar tendencias y patrones, y ajustar estas tendencias y estacionalidades para crear series estacionarias. Las fluctuaciones irregulares restantes se modelan como observaciones independientes e idénticamente distribuidas (iid) mediante regresión lineal sobre variables exógenas.

• Este enfoque mejora las predicciones futuras. La metodología se presenta en un diagrama de flujo y se cubren los primeros tres pasos, incluyendo procesamiento avanzado de datos, pruebas estadísticas para estacionariedad y descomposición de series temporales. Estos conceptos son fundamentales para desarrollar modelos predictivos de series temporales.

1.21. Procesamiento avanzado y visualización de datos de series temporales

Introducción

• Las series temporales suelen transformarse en estadísticos agregados como la media o la mediana para períodos de tiempo más largos. Por ejemplo, en ventas mensuales de automóviles, la estacionalidad mensual se resalta al calcular promedios para cada mes a lo largo de varios años. Esto se logra dividiendo la serie en segmentos mensuales y agregando los datos de cada segmento.

• Para un análisis más detallado, a menudo se utilizan agregados móviles, como medias trimestrales, que se calculan desplazando una ventana de tiempo sobre la serie y calculando estadísticos dentro de esa ventana. Esto se demuestra con ejemplos de remuestreo, agrupación y cálculo de estadísticos móviles utilizando librerías de pandas.

1.22. Remuestreo de datos de series temporales

• La técnica de remuestreo se ilustra utilizando una serie temporal sobre concentraciones químicas tomadas cada dos horas entre el 1 de enero de 1975 y el 17 de enero de 1975. El conjunto de datos se ha descargado de datamarket.

import pandas as pd
import numpy as np
from matplotlib import pyplot as plt

• A continuación se leen los datos del archivo CSV en un pandas.DataFrame y mostramos las primeras filas del DataFrame

df = pd.read_csv('/home/lihkir/Data/chemical-concentration-readings.csv')
print('Shape of the dataset:', df.shape)
df.head()

Shape of the dataset: (197, 2)

	Timestamp	Chemical conc.
0	1975-01-01 00:00:00	17.0
1	1975-01-01 02:00:00	16.6
2	1975-01-01 04:00:00	16.3
3	1975-01-01 06:00:00	16.1
4	1975-01-01 08:00:00	17.1

• Convertiremos las observaciones de la serie temporal original en medias diarias aplicando las funciones de remuestreo y media en la segunda columna. La función de remuestreo requiere que los índices de fila del DataFrame sean timestamp de tipo numpy.datetime64.

• Por lo tanto, cambiamos los índices de fila de números enteros, como se muestra en la tabla anterior, a datetime_rowid que es una pandas.Series de objetos numpy.datetime64.

• Los objetos numpy.datetime64 se generan a partir de la columna Timestamp utilizando la función de utilidad pd.todatetime. El siguiente código muestra cómo se realiza la reindexación por filas

datetime_rowid = df['Timestamp'].map(lambda t: pd.to_datetime(t, format='%Y-%m-%d %H:%M:%S'))
df.index = datetime_rowid
df.head()

	Timestamp	Chemical conc.
Timestamp
1975-01-01 00:00:00	1975-01-01 00:00:00	17.0
1975-01-01 02:00:00	1975-01-01 02:00:00	16.6
1975-01-01 04:00:00	1975-01-01 04:00:00	16.3
1975-01-01 06:00:00	1975-01-01 06:00:00	16.1
1975-01-01 08:00:00	1975-01-01 08:00:00	17.1

• Ahora estamos listos para aplicar las funciones de resample y mean en la columna Chemical conc.

daily = df['Chemical conc.'].resample('D')
daily_mean = daily.mean()

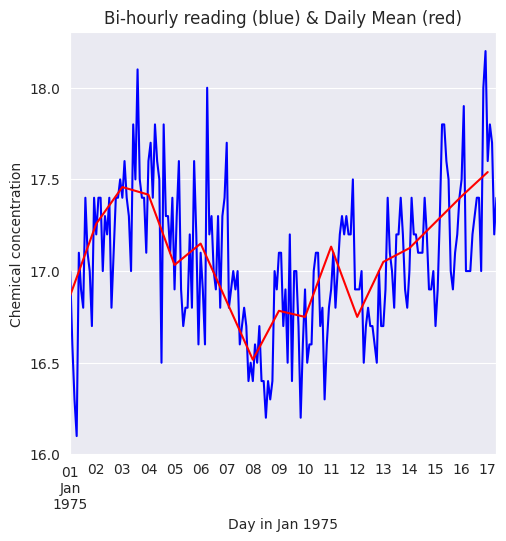
• Observe que hemos pasado el argumento D a la función resample para generar las medias diarias. Para los agregados mensuales y anuales, tenemos que pasar M e Y a la función resample. Por último, las medias originales y diarias se representan en la siguiente figura, que muestra el efecto de suavización de esta última.

fig = plt.figure(figsize=(5.5, 5.5))
ax = fig.add_subplot(1,1,1)
df['Chemical conc.'].plot(ax=ax, color='b')
daily_mean.plot(ax=ax, color='r')
ax.set_title('Bi-hourly reading (blue) & Daily Mean (red)');
ax.set_xlabel('Day in Jan 1975');
ax.set_ylabel('Chemical concentration');

1.23. Agregación por grupos

• Para demostrar la agregación por grupos, utilizaremos la serie temporal de la temperatura media diaria del río Fisher en Texas, Estados Unidos. La serie temporal tiene observaciones tomadas entre el 1 de enero de 1988 y el 31 de diciembre de 1991.

df = pd.read_csv('/home/lihkir/Data/mean-daily-temperature-fisher-river.csv')
df.index = df['Date'].map(lambda d: pd.to_datetime(d, format = '%Y-%m-%d'))

print('Shape of dataframe:', df.shape)
df.head()

Shape of dataframe: (1461, 2)

	Date	Mean temperature
Date
1988-01-01	1988-01-01	-23.0
1988-01-02	1988-01-02	-20.5
1988-01-03	1988-01-03	-22.0
1988-01-04	1988-01-04	-30.5
1988-01-05	1988-01-05	-31.0

fig = plt.figure(figsize=(5.5, 5.5))
ax = fig.add_subplot(1,1,1)
df['Mean temperature'].plot(ax=ax, color='b')
ax.set_title('Mean daily temperature');

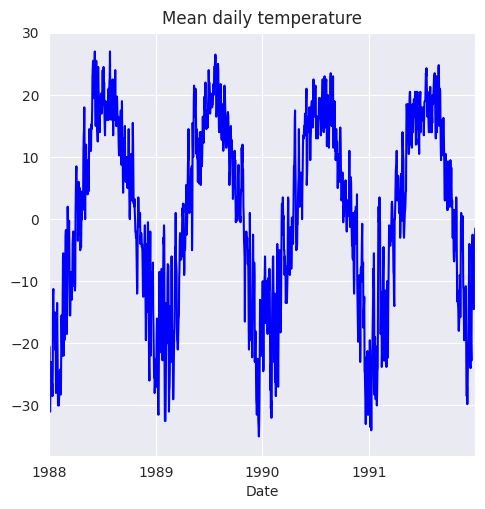
• La serie temporal original parece tener patrones mensuales que se repiten cada año y que pueden verificarse calculando los promedios mensuales. Esto se hace agrupando los datos en 12 meses y luego calculando los promedios de cada mes. Comenzamos agregando una columna Month_Year al DataFrame

df['Month_Year'] = df.index.map(lambda d: d.strftime('%m-%Y'))
df.head()

	Date	Mean temperature	Month_Year
Date
1988-01-01	1988-01-01	-23.0	01-1988
1988-01-02	1988-01-02	-20.5	01-1988
1988-01-03	1988-01-03	-22.0	01-1988
1988-01-04	1988-01-04	-30.5	01-1988
1988-01-05	1988-01-05	-31.0	01-1988

• A continuación, la columna Mean temperature se agrupa con respecto a la nueva columna Month_Year y se calculan la media, la mediana y las desviaciones estándar de cada mes

monthly_stats = df.groupby(by='Month_Year')['Mean temperature'].aggregate([np.mean, np.median, np.std])
monthly_stats.reset_index(inplace=True)
monthly_stats.head()

	Month_Year	mean	median	std
0	01-1988	-22.137097	-23.0	5.260640
1	01-1989	-17.129032	-18.0	8.250725
2	01-1990	-15.112903	-12.0	6.606764
3	01-1991	-23.038710	-24.5	7.095570
4	02-1988	-19.025862	-19.5	8.598522

• Tenga en cuenta que las filas de la tabla anterior no están en orden ascendente de Month_Year. Por lo tanto, es necesario registrarlo. Esto se hace creando dos nuevas columnas Month y Year y, a continuación, ordenando en orden ascendente Year, seguido de la ordenación en orden ascendente de Month

monthly_stats['Year'] = monthly_stats['Month_Year']\
.map(lambda m: pd.to_datetime(m, format='%m-%Y').strftime('%Y'))

monthly_stats['Month'] = monthly_stats['Month_Year']\
.map(lambda m: pd.to_datetime(m, format='%m-%Y').strftime('%m'))

monthly_stats.sort_values(by=['Year', 'Month'], inplace=True)
monthly_stats.head()

	Month_Year	mean	median	std	Year	Month
0	01-1988	-22.137097	-23.000	5.260640	1988	01
4	02-1988	-19.025862	-19.500	8.598522	1988	02
8	03-1988	-8.258065	-9.250	5.341459	1988	03
12	04-1988	2.641667	1.875	5.057720	1988	04
16	05-1988	11.290323	11.000	6.254364	1988	05

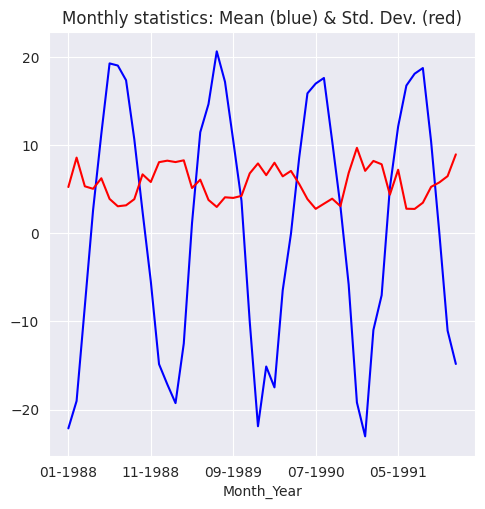
• Los agregados mensuales se representan en la siguiente figura, que pone de manifiesto la estacionalidad mensual existente en los datos originales.

monthly_stats.index = monthly_stats['Month_Year']

fig = plt.figure(figsize=(5.5, 5.5))
ax = fig.add_subplot(1,1,1)

monthly_stats['mean'].plot(ax=ax, color='b')
monthly_stats['std'].plot(ax=ax, color='r')

ax.set_title('Monthly statistics: Mean (blue) & Std. Dev. (red)');

1.24. Estadísticos móviles

Introducción

• Los estadísticos móviles o rodantes se calculan desplazando una ventana sobre la serie temporal original y agregando los datos de cada ventana. Los parámetros clave son el tamaño de la ventana y la longitud del paso, que definen la entrada y el intervalo para cada cálculo.

• Por ejemplo, supongamos que se utiliza un tamaño de ventana de \(k\) y un intervalo de longitud \(l\) para calcular la función \(f\) sobre una serie temporal \(y_{1}, y_{2},\dots, y_{T}\) con \(T\) observaciones. En este caso, el estadístico móvil se obtiene como \(f(y_{1}, y_{2},\dots, y_{k}), f(y_{1+l}, y_{2+l},\dots, y_{k+l})\), y así sucesivamente.

• Obsérvese que cada vez se calcula la función desplazando la ventana temporal hacia la derecha en \(l\) unidades de tiempo. La media móvil es un caso especial de la función \(f\) y requiere simplemente promediar las observaciones en la ventana de tiempo.

• Vamos a demostrar cómo se pueden calcular las medias móviles en el conjunto de datos de Fisher River. Calcularemos las medias móviles semanales, fijando el tamaño de la ventana en siete y deslizando la ventana un lugar a la derecha

weekly_moving_average = df['Mean temperature'].rolling(7).mean()

monthly_moving_average = df['Mean temperature'].rolling(30).mean()

• La función rolling solo toma como argumento el tamaño de la ventana. Por lo tanto, para añadir una longitud de paso de más de uno, seguimos calculando la media móvil como se ha mostrado anteriormente, pero cortamos la serie resultante para obtener el resultado deseado. Para las franjas de más de dos unidades de tiempo utilizamos el siguiente código

weekly_moving_average_2stride = df['Mean temperature'].rolling(7).mean()[::2]

monthly_moving_average_2stride = df['Mean temperature'].rolling(30).mean()[::2]

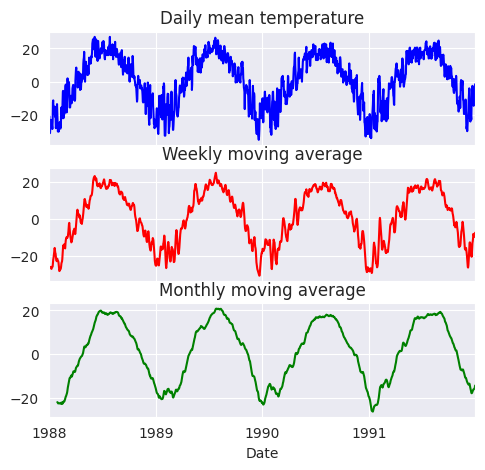
• En el análisis de series temporales, los estadísticos móviles basadas en la longitud de paso son las más comunes, por lo que rara vez se necesitará algo más que la función rolling. Los datos originales se representan en la siguiente figura, que muestra la reducción del ruido y el consiguiente efecto de suavización producido por las medias móviles

fig, axarr = plt.subplots(3, sharex=True)
fig.set_size_inches(5.5, 5,5)

df['Mean temperature'].plot(ax=axarr[0], color='b')
axarr[0].set_title('Daily mean temperature');

weekly_moving_average.plot(ax=axarr[1], color='r')
axarr[1].set_title('Weekly moving average');

monthly_moving_average.plot(ax=axarr[2], color='g')
axarr[2].set_title('Monthly moving average');

Theorem 1.1

• Una media móvil simple de longitud \(N\) asigna ponderaciones \(1/N\) a las observaciones más recientes \(y_{T}, y_{T-1},\dots, y_{T-N+1}\), y peso cero a todas las demás observaciones. Si \(M_{T}\) es la media móvil, la media móvil de \(N\) intervalos en el período \(T\) es

\[ M_{T}=\frac{y_{T}+y_{T-1}+\cdots+y_{T-N+1}}{N}=\frac{1}{N}\sum_{t=T-N+1}^{T}y_{t} \]

• Evidentemente, a medida que se dispone de cada nueva observación, ésta se añade a la suma a partir de la cual se calcula la media móvil y la observación más antigua se descarta (rolling). Si la varianza de una observación individual \(y_{t}\) es \(\sigma^{2}\), entonces, suponiendo que las observaciones no están correlacionadas, la varianza de la media móvil es

\[ \textsf{Var}(M_{T})=\frac{\sigma^{2}}{N}. \]

• A veces se utiliza una versión "centrada" de la media móvil, dada por

  \[ M_{t}=\frac{1}{S+1}\sum_{i=-S}^{S}y_{t-i} \]

  donde el intervalo de la media móvil centrada es \(N=2S+1\)

Demostración

• Si la varianza de una observación individual \(y_{t}\) es \(\sigma^{2}\), entonces asumiendo que las observaciones no están correlacionadas, la varianza de la media móvil es

\[ \textsf{Var}\left(M_{T}\right)=\textsf{Var}\left(\frac{1}{N}\sum_{t=T-N+1}^{T}y_{t}\right)=\frac{1}{N^2}\sum_{t=T-N+1}^{T}\textsf{Var}(y_{t})=\frac{\sigma^2}{N}. \]

Observación

• La media móvil simple es un suavizador de datos lineal, o un filtro lineal, porque sustituye cada observación \(y_{t}\) por una combinación lineal de los otros puntos de datos que están cerca de él en el tiempo. Si los pesos de la combinación lineal son iguales, la combinación lineal es una media.

• En algunos caso, podrían utilizarse pesos desiguales. Por ejemplo, el filtro de Hanning es una media móvil ponderada y centrada dada por

  \[\begin{split} \\[2mm] M_{t}^{H}=0.25 y_{t+1}+0.5y_{t}+0.25y_{t-1}. \end{split}\]

  Julius von Hann, meteorólogo austriaco del siglo XIX, utilizó este filtro para suavizar datos meteorológicos.

• Una desventaja obvia de un filtro lineal como una media móvil es que un punto de datos inusual o erróneo o un valor atípico dominará las medias móviles que contengan esa observación, contaminando las medias durante un periodo de tiempo igual al intervalo del filtro. Por ejemplo, consideremos la secuencia de observaciones

  (1.2)\[\begin{split} \\[1mm] \{15, 18, 13, 12, 16, 14, 16, 17, 18, 15, 18, 200, 19, 14, 21, 24, 19, 25\} \end{split}\]

  que aumenta de forma razonablemente constante de 15 a 25, excepto para el inusual valor 200.

• Cualquier versión suavizada razonable de los datos también debería aumentar de forma constante de 15 a 25 y no hacer hincapié en el valor 200. Ahora, incluso si 200 es una observación legítima, y no el resultado de un error de registro de datos (¡quizás debería ser 20!), es tan inusual que merece una atención especial y probablemente no debería analizarse junto con el resto de los datos.

Definition 1.1 (Medianas moviles corridas)

• Las medianas móviles impares (también denominadas medianas móviles corridas) son una alternativa a las medias móviles que suavizan eficazmente los datos cuando la serie puede estar contaminada con valores inusuales o valores atípicos. La mediana de intervalo \(N\) se define como

  \[ m_{t}^{[N]}=\textsf{med}(y_{t-u},\dots,y_{t},\dots,\dots,y_{t+u}), \]

  donde \(N=2u+1\).

• La mediana es la observación intermedia en el orden de clasificación (u orden de valor). La mediana móvil de span 3 es un suavizador de datos muy popular y eficaz, donde

  \[ m_{t}^{3}=\textsf{med}(y_{t-1}, y_{t}, y_{t+1}). \]

• Este suavizador procesaría los datos de tres en tres, y sustituiría las tres observaciones originales por su mediana. Si aplicamos este suavizador a los datos anteriores (ver datos (1.2)), obtenemos

\[ \{\underline{\hspace{9mm}},15, 13, 13, 14, 16, 17, 17, 18, 18, 19, 19, 19, 21, 21, 24, \underline{\hspace{9mm}}\} \]

• Estos datos suavizados son una representación razonable de los datos originales, pero ignoran convenientemente el valor 200. Los valores iniciales/finales se pierden al utilizar la mediana móvil, y se representan con “\(\underline{\hspace{9mm}}\)”.

• En general, una mediana móvil pasará secuencias monótonas de datos sin cambios. Seguirá una función escalonada en los datos, pero eliminará un pico o una alteración más persistente en los datos que tenga una duración de como máximo \(u\) observaciones consecutivas. Las medianas móviles pueden aplicarse más de una vez para obtener una serie de observaciones aún más suave.

• Por ejemplo, si se aplica la mediana móvil de longitud 3 a los datos suavizados anteriores, resulta en

\[ \{\underline{\hspace{9mm}}, 13, 13, 14, 16, 17, 17, 18, 18, 19, 19, 19, 21, 21, \underline{\hspace{9mm}}\} \]

• Estos datos son ahora tan suaves como se puede conseguir; es decir, la aplicación repetida de la mediana móvil no cambiará los datos, aparte de los valores finales. Si hay muchas observaciones, la pérdida de información de los valores finales que faltan no es grave. Sin embargo, si es necesario o deseable mantener las longitudes de los conjuntos de datos originales y suavizados, una forma sencilla de hacerlo es “copiar” o volver a añadir los valores finales de los datos originales. Esto daría como resultado los datos suavizados:

\[ \{\underline{\hspace{9mm}}, 15, 18, 13, 13, 14, 16, 17, 17, 18, 18, 19, 19, 19, 21, 21, 19, 25, \underline{\hspace{9mm}}\} \]

• También existen métodos para suavizar los valores finales. [Tukey and others, 1977] es una referencia básica sobre este tema y contiene muchas otras técnicas útiles para el análisis de datos.

1.25. Procesos estacionarios

• La estacionariedad es un supuesto fundamental en la teoría estadística y el análisis de series temporales. Asegura que los estadísticos muestrales, como la media y la varianza, se mantengan constantes a lo largo del tiempo, lo que permite su uso como estimaciones confiables para futuras ocurrencias.

• En el contexto de series temporales, la estacionariedad implica que las propiedades de la serie, como: la media, la varianza y la autocorrelación, no cambien con el tiempo. En resumen, la estacionariedad requiere que la serie tenga una media y una varianza constantes, sin patrones predecibles o repetitivos.

Definition 1.2 (Serie temporal estacionaria)

• Una serie de tiempo se dice que es estrictamente estacionaria si sus propiedades no se ven afectadas por un cambio en el origen temporal. Es decir, si la distribución de probabilidad conjunta de las observaciones \(y_{t}, y_{t+1}, y_{t+2}, \dots, y_{t+n}\) es exactamente igual a la distribución de las observaciones \(y_{t+k}, y_{t+k+1}, y_{t+k+2}, \dots, y_{t+k+n}\) entonces la es estrictamente estacionaria.

• Cuando \(n = 0\), el supuesto de estacionariedad significa que la distribución de probabilidad de \(y_{t}\) es la misma en todos los periodos de tiempo y puede escribirse como \(f(y)\).

• Estacionarieda implica un tipo de equilibrio estadístico o estabilidad en los datos. En consecuencia, la serie temporal tiene una media constante definida de la forma habitual como

  \[ \mu_{y}=\textsf{E}(y)=\int_{-\infty}^{\infty}yf(y)dy \]

  y una varianza constante definida como

  \[\begin{split} \\[1mm] \sigma_{y}^{2}=\textsf{Var}(y)=\int_{-\infty}^{\infty}(y-\mu_{y})^{2}f(y) dy. \end{split}\]

• Para estimar estos parámetros se utilizan la media y la varianza muestrales. Si las observaciones de la serie temporal son \(y_{1}, y_{2},\dots, y_{T}\), la media muestral es

  \[ \overline{y}=\hat{\mu}_{y}=\frac{1}{T}\sum_{t=1}^{T}y_{t} \]

  y la varianza muestral es

  (1.3)\[ s^{2}=\hat{\sigma}_{y}^{2}=\frac{1}{T}\sum_{t=1}^{T}(y_{t}-\overline{y})^{2}. \]

• Obsérvese que el divisor en la Ecuación (1.3) es \(T\) en lugar del más familiar \(T-1\). Esta es la convención común en muchas aplicaciones de series temporales, como \(T\) no suele ser pequeño, habrá poca diferencia entre utilizar \(T\) en lugar de \(T-1\).

• Un ejemplo popular de serie temporal estacionaria es la serie de media cero, que se genera a partir de puntos que se muestrean de una distribución normal de media cero y varianza unitaria.

• Aunque los puntos se muestrean secuencialmente de la distribución normal y se representan como una serie temporal, las observaciones individuales son independientes e idénticamente distribuidas (iid). La serie de media cero no muestra ningún patrón temporal, como la tendencia, la estacionalidad y la autocorrelación.

from random import seed
from pandas import Series
import random 
from pandas.plotting import autocorrelation_plot
import matplotlib.pyplot as plt

• Usamos una semilla seed generadora de números aleatorios, y creamos una serie de ruido blanco

seed(1)
series = [random.gauss(0.0, 1.0) for i in range(1000)]
series = Series(series)
series.describe()

count    1000.000000
mean       -0.013222
std         1.003685
min        -2.961214
25%        -0.684192
50%        -0.010934
75%         0.703915
max         2.737260
dtype: float64

series.plot(alpha=0.7);

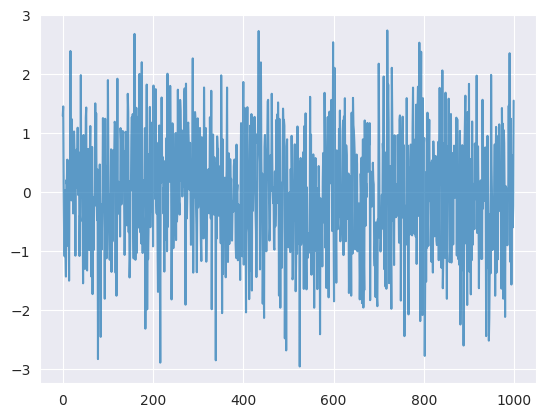
plt.rcParams['text.usetex'] = True
fig, axs = plt.subplots(3, 2, figsize=(8, 10))

for i, ax in enumerate(axs.flat):
    ax.hist(series[i:], bins=30, alpha=0.7)
    ax.set_title(r'Histogram $\{y_{t+%d}\}_{t=1}^{T}$' % (i)) 

plt.tight_layout()
plt.show()
plt.rcParams['text.usetex'] = False

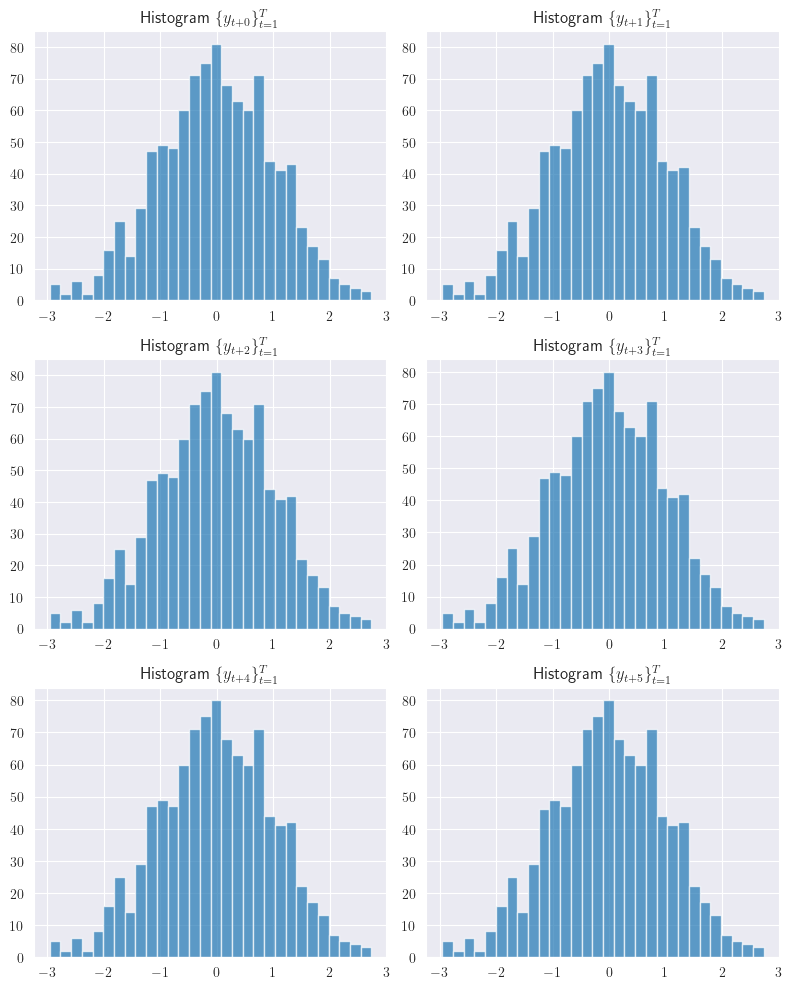
• Las series temporales reales suelen no ser estacionarias debido a tendencias y estacionalidades que afectan a la media, la varianza y la autocorrelación a lo largo del tiempo. Las fluctuaciones cíclicas no se consideran al definir la estacionariedad, ya que estas solo pueden explicarse mediante variables exógenas (variables o factores externos).

• Una serie temporal sin patrones predecibles a largo plazo es considerada estacionaria. Para verificar esto, se utiliza la prueba de Dickey-Fuller Aumentada (ADF) y se aplica la diferenciación para estacionarizar series temporales no estacionarias, eliminando tendencias y componentes estacionales. Los métodos de descomposición para tendencias y estacionalidades complejas se discuten a continuación.

1.26. Transformación de datos y ajustes

• Las transformaciones de datos son comunes en estadística y se utilizan principalmente para estabilizar la varianza de los datos. La varianza no constante, conocida como heteroscedasticidad, es frecuente en series temporales. Para abordar esto, se emplean modelos como GARCH. Ejemplos incluyen series relacionadas con la volatilidad de acciones como Tesla o la criptomoneda BTC, donde una transformación logarítmica puede reducir la varianza.

Definition 1.3 (Transformaciones de potencia)

• Un tipo muy popular de transformación de datos para tratar con la varianza es la familia de transformaciones de potencia, dada por

  \[\begin{split} y^{(\lambda)}= \begin{cases} \frac{\displaystyle{y^{\lambda}-1}}{\displaystyle{\lambda\dot{y}^{\lambda-1}}}, &\quad\lambda\neq0\\[2mm] \dot{y}\lambda y, &\quad\lambda=0 \end{cases},\quad\text{donde}\quad\dot{y}=\exp\left[\frac{1}{T}\sum_{t=1}^{T}\ln(y_{t})\right]. \end{split}\]

  \(\dot{y}\) es conocida como la media geométrica de las observaciones.

Observación

• Si \(\lambda=1\), no hay transformación. Los valores típicos de \(\lambda\) utilizados con datos de series temporales son:

  1. \(\lambda=0.5\) (transformación de raíz cuadrada)

  2. \(\lambda=0\) (transformación logarítmica \((y^{\lambda}-1)/\lambda\rightarrow\log(y)\) cuando \(\lambda\rightarrow 0\))

  3. \(\lambda=-0.5\) (transformación recíproca de raíz cuadrada)

  4. \(\lambda=-1\) (transformación inversa).

• El divisor es un factor de escala que permite comparar la suma residual de cuadrados al ajustar diferentes modelos con diferentes transformaciones. La transformación logarítmica se usa cuando la variabilidad de la serie temporal original aumenta con su nivel medio, siendo óptima cuando la desviación típica aumenta linealmente con la media.

• La transformación logarítmica también tiene una interpretación física como cambio porcentual. Para ilustrarlo, considere la serie de tiempo \(y_{1}, y_{2}, \dots, y_{T}\) y supongamos que estamos interesados en el porcentaje de cambio en \(y_{t}\), digamos,

\[ x_{t}=\frac{100(y_{t}-y_{t-1})}{y_{t-1}}. \]

• El cambio porcentual aproximado de \(y_{t}\) puede calcularse a partir de las diferencias de la serie temporal transformada logarítmicamente \(x_{t}\cong 100[\ln(y_{t}) - \ln(y_{t}-1)]\) dado que,

  \[\begin{split} \\[1mm] \begin{align*} 100[\ln(y_{t}) - \ln(y_{t}-1)]&=100\ln\left(\frac{y_{t}}{y_{t-1}}\right)\\ &=100\ln\left(\frac{y_{t-1}+(y_{t}-y_{t-1})}{y_{t-1}}\right)\\ &=100\ln\left(1+\frac{x_{t}}{100}\right)\cong x_{t}, \end{align*} \end{split}\]

  nótese que \(\ln(1+z)\cong z\) cuando \(z\) es pequeño.

1.27. Ajustes estacionales y de tendencia

• Los ajustes de tendencia y estacionales son esenciales en el modelado y la predicción de series temporales. Una serie temporal con tendencia se considera no estacionaria. Para simplificar el análisis, es común eliminar la tendencia ajustando los datos a un modelo de regresión y luego sustraerlo de las observaciones originales, dejando residuos sin tendencia.

1.28. Diferenciación

• Otro enfoque para eliminar la tendencia es mediante la diferenciación de los datos; es decir, aplicando el operador de diferencia a la serie temporal original para obtener una nueva serie temporal, digamos,

  \[ x_{t}=y_{t}-y_{t-1}=\nabla y_{t}, \]

  donde \(\nabla\) es el operador de diferencia (backward). Otra forma de escribir la operación de diferencia es en términos de un operador de desplazamiento hacia atrás (backshift operator) \(B\), definido como \(By_{t} = y_{t-1}\), entonces

  \[ x_{t}=(1-B)y_{t}=\nabla y_{t}=y_{t}-y_{t-1} \]

  con \(\nabla=(1-B)\).

• La diferenciación puede realizarse sucesivamente si es necesario hasta que se elimine la tendencia; por ejemplo, la segunda diferencia es

  \[ x_{t}=\nabla^{2}y_{t}=\nabla(\nabla y_{t})=(1-B)^{2}y_{t}=(1-2B+B^{2})=y_{t}-2y_{t-1}+y_{t-2} \]

• En general, las potencias del operador de desplazamiento y diferencia hacia atrás se definen como

  \[ B^{d}y_{t}=y_{t-d}\quad\text{y}\quad\nabla^{d}=(1-B)^{d}. \]

• La diferenciación se usa para eliminar la estacionalidad en series temporales que tienen tanto tendencia como componentes estacionales. Se define un operador de diferencia estacional con rezago \(d\) como

  \[ \nabla_{d}y_{t}=(1-B^{d})=y_{t}-y_{t-d}. \]

• Por ejemplo, si tuviéramos datos mensuales con una estación anual (una situación muy común), es probable que usemos \(d=12\), por lo que los datos diferenciados estacionalmente serían

  \[ \nabla_{12}y_{t}=(1-B^{12})y_{t}=y_{t}-y_{t-12} \]

• Cuando hay tendencia y componentes estacionales al mismo tiempo, podemos eliminarlos diferenciando primero estacionalmente y luego usando la diferenciación regular para eliminar la tendencia.

Observación

• La diferenciación es más simple que ajustar un modelo de tendencia porque no necesita estimar parámetros. Además, mientras que el ajuste del modelo supone que la tendencia es constante en el tiempo, la diferenciación permite que cambie. La primera diferencia considera cambios en la media, la segunda en la pendiente, y así sucesivamente. Por lo general, una o dos diferencias son suficientes para eliminar una tendencia en los datos.

• Para verificar si la diferenciación de primer orden ha estacionado una serie temporal, se puede trazar la función de autocorrelación (ACF) y realizar la prueba de Ljung-Box en la serie diferenciada. Esta prueba determina si la autocorrelación observada es estadísticamente significativa, con la hipótesis nula de que la serie es aleatoria y sin autocorrelación predecible.

• Ilustraremos esto con la serie temporal del índice industrial Dow Jones (DJIA), tomando la primera diferencia de los valores de cierre y trazando la serie resultante.

import pandas as pd
import numpy as np
from statsmodels.tsa import stattools
from matplotlib import pyplot as plt
from pandas.plotting import autocorrelation_plot

djia_df = pd.read_excel('/home/lihkir/Data/DJIA_Jan2016_Dec2016.xlsx')
djia_df.head()

	Date	Open	High	Low	Close	Adj Close	Volume
0	2016-01-04	17405.480469	17405.480469	16957.630859	17148.939453	17148.939453	148060000
1	2016-01-05	17147.500000	17195.839844	17038.609375	17158.660156	17158.660156	105750000
2	2016-01-06	17154.830078	17154.830078	16817.619141	16906.509766	16906.509766	120250000
3	2016-01-07	16888.359375	16888.359375	16463.630859	16514.099609	16514.099609	176240000
4	2016-01-08	16519.169922	16651.890625	16314.570313	16346.450195	16346.450195	141850000

• Analicemos la columna Date y utilicémosla como índice de fila para el DataFrame y dejémosla como columna

djia_df['Date'] = pd.to_datetime(djia_df['Date'], '%Y-%m-%d')
djia_df.index = djia_df['Date']
djia_df.drop('Date', axis=1, inplace=True)
djia_df.head()

	Open	High	Low	Close	Adj Close	Volume
Date
2016-01-04	17405.480469	17405.480469	16957.630859	17148.939453	17148.939453	148060000
2016-01-05	17147.500000	17195.839844	17038.609375	17158.660156	17158.660156	105750000
2016-01-06	17154.830078	17154.830078	16817.619141	16906.509766	16906.509766	120250000
2016-01-07	16888.359375	16888.359375	16463.630859	16514.099609	16514.099609	176240000
2016-01-08	16519.169922	16651.890625	16314.570313	16346.450195	16346.450195	141850000

• Utilizaremos los valores "Close" del DJIA para ilustrar la diferenciación

first_order_diff = djia_df['Close'].diff(1)

• Trazamos las series temporales originales y las de primera diferencia

fig, ax = plt.subplots(2, sharex=True)
fig.set_size_inches(5.5, 5.5)
djia_df['Close'].plot(ax=ax[0], color='b');
ax[0].set_title('Close values of DJIA during Jan 2016-Dec 2016');
first_order_diff.plot(ax=ax[1], color='r');
ax[1].set_title('First-order differences of DJIA during Jan 2016-Dec 2016');

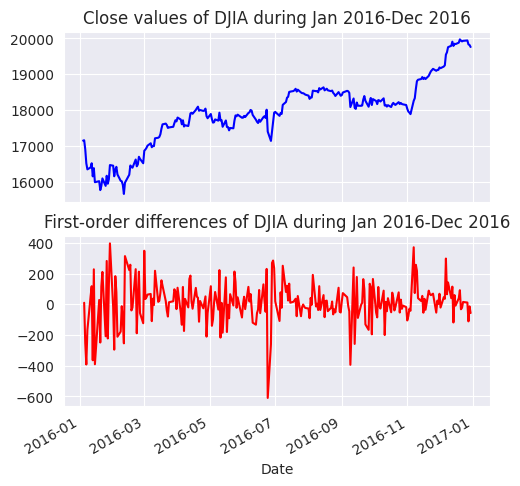
• A continuación, se calcula el ACF para diferentes rezagos y se verifica la prueba de Ljung-Box. La figura siguiente muestra la ACF de los valores de cierre del DJIA y también para la serie temporal de diferencias de primer orden.

• Obsérvese que para las series diferenciadas, la ACF no muestra un patrón predecible y cae repentinamente cerca de cero. Además, el valor \(p\) de la prueba nos hace aceptar la hipótesis nula de la prueba de Ljung-Box (aleatoriedad e independencia) para las series diferenciadas

fig, ax = plt.subplots(2, sharex=True)
fig.set_size_inches(5.5, 5.5)
autocorrelation_plot(djia_df['Close'], color='b', ax=ax[0])
ax[0].set_title('ACF of DJIA Close values')
autocorrelation_plot(first_order_diff.iloc[1:], color='r', ax=ax[1])
ax[1].set_title('ACF of first differences of DJIA Close values')
plt.tight_layout(pad=0.4, w_pad=0.5, h_pad=2.0)

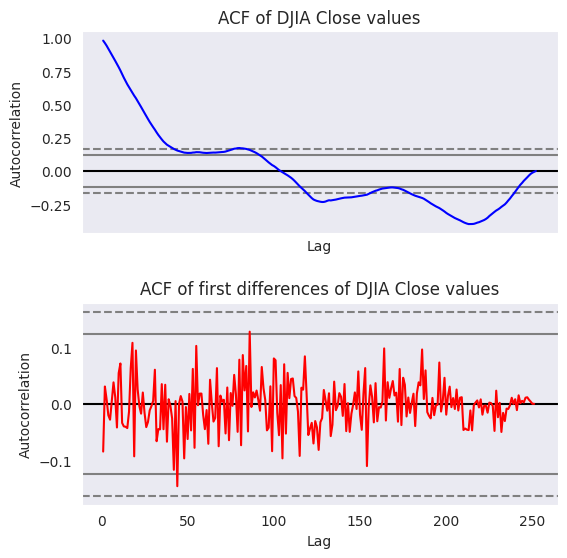
• Para la prueba de Ljung-Box, utilizamos la función acf del paquete statsmodels.tsa.stattools. La función acf está hecha para devolver las autocorrelaciones, los intervalos de confianza, los estadísticos \(Q\) y los valores \(p\) de la prueba

acf_djia, confint_djia, qstat_djia, pvalues_djia = stattools.acf(djia_df['Close'],
                                                                 nlags=20,
                                                                 qstat=True,
                                                                 alpha=0.05)

• Comprobemos si con un nivel de confianza del 95% (\(\alpha=0.05\)) si se rechaza la hipótesis nula en cualquiera de los rezagos para los valores no diferenciados del DJIA Close

\[\begin{split} \begin{align*} H_{0}:\quad & \text{No hay autocorrelación significativa a diferentes rezagos}~k~(\rho_{k}=0)\\[2mm] H_{1}:\quad & \text{Existe autocorrelación significativa en al menos un rezago}~k~(\rho_{k}\neq0) \end{align*} \end{split}\]

alpha = 0.05
for l, p_val in enumerate(pvalues_djia):
    if p_val > alpha:
        print('Null hypothesis is accepted at lag = {} for p-val = {}'.format(l, p_val))
    else:
        print('Null hypothesis is rejected at lag = {} for p-val = {}'.format(l, p_val))

Null hypothesis is rejected at lag = 0 for p-val = 2.857506276385174e-55
Null hypothesis is rejected at lag = 1 for p-val = 1.7871763971271254e-105
Null hypothesis is rejected at lag = 2 for p-val = 9.927155881909959e-154
Null hypothesis is rejected at lag = 3 for p-val = 8.084096278834598e-200
Null hypothesis is rejected at lag = 4 for p-val = 9.125287802249553e-244
Null hypothesis is rejected at lag = 5 for p-val = 1.0907828815951678e-285
Null hypothesis is rejected at lag = 6 for p-val = 0.0
Null hypothesis is rejected at lag = 7 for p-val = 0.0
Null hypothesis is rejected at lag = 8 for p-val = 0.0
Null hypothesis is rejected at lag = 9 for p-val = 0.0
Null hypothesis is rejected at lag = 10 for p-val = 0.0
Null hypothesis is rejected at lag = 11 for p-val = 0.0
Null hypothesis is rejected at lag = 12 for p-val = 0.0
Null hypothesis is rejected at lag = 13 for p-val = 0.0
Null hypothesis is rejected at lag = 14 for p-val = 0.0
Null hypothesis is rejected at lag = 15 for p-val = 0.0
Null hypothesis is rejected at lag = 16 for p-val = 0.0
Null hypothesis is rejected at lag = 17 for p-val = 0.0
Null hypothesis is rejected at lag = 18 for p-val = 0.0
Null hypothesis is rejected at lag = 19 for p-val = 0.0

• Obtengamos los intervalos de confianza, los estadísticos \(Q\) de Ljung-Box y los valores \(p\) para los valores diferenciados del DJIA Close

acf_first_diff, confint_first_diff,\
qstat_first_diff, pvalues_first_diff = stattools.acf(first_order_diff.iloc[1:],
                                                     nlags=20,
                                                     qstat=True,
                                                     alpha=0.05)

• Comprobemos si con un nivel de confianza del 95% (\(\alpha = 0.05\)) si se rechaza la hipótesis nula en cualquiera de los rezagos

alpha = 0.05
for l, p_val in enumerate(pvalues_first_diff):
    if p_val > alpha:
        print('Null hypothesis is accepted at lag = {} for p-val = {}'.format(l, p_val))
    else:
        print('Null hypothesis is rejected at lag = {} for p-val = {}'.format(l, p_val))

Null hypothesis is accepted at lag = 0 for p-val = 0.17742519268365267
Null hypothesis is accepted at lag = 1 for p-val = 0.35711074717194824
Null hypothesis is accepted at lag = 2 for p-val = 0.5569664476694898
Null hypothesis is accepted at lag = 3 for p-val = 0.7025937592112144
Null hypothesis is accepted at lag = 4 for p-val = 0.7937258941281413
Null hypothesis is accepted at lag = 5 for p-val = 0.880645293990265
Null hypothesis is accepted at lag = 6 for p-val = 0.9058055508095895
Null hypothesis is accepted at lag = 7 for p-val = 0.9461503874902826
Null hypothesis is accepted at lag = 8 for p-val = 0.9529107001186853
Null hypothesis is accepted at lag = 9 for p-val = 0.9452880323047996
Null hypothesis is accepted at lag = 10 for p-val = 0.9103701842715781
Null hypothesis is accepted at lag = 11 for p-val = 0.9303312940619602
Null hypothesis is accepted at lag = 12 for p-val = 0.9412519715905938
Null hypothesis is accepted at lag = 13 for p-val = 0.9498882104867831
Null hypothesis is accepted at lag = 14 for p-val = 0.9556341186857322
Null hypothesis is accepted at lag = 15 for p-val = 0.9708115886391275
Null hypothesis is accepted at lag = 16 for p-val = 0.9617513839353877
Null hypothesis is accepted at lag = 17 for p-val = 0.8766266334022736
Null hypothesis is accepted at lag = 18 for p-val = 0.7968569568190992
Null hypothesis is accepted at lag = 19 for p-val = 0.7023038219602964

• Examinaremos ahora la serie temporal de las temperaturas medias diarias del río Fisher para demostrar el efecto de la diferenciación estacional. La serie original y la media mensual muestran un comportamiento estacional evidente.

• Se calcula la autocorrelación de la media mensual y se traza utilizando la función autocorrelation_plot de pandas.plotting. Esta función es útil para identificar la autocorrelación significativa en una serie temporal y muestra intervalos de confianza del 95% y 99%. La ACF de las temperaturas medias mensuales oscila dentro y fuera de los intervalos de confianza del 99%, indicando que la serie no es estacionaria debido a la estacionalidad.

daily_temp = pd.read_excel('/home/lihkir/Data/mean-daily-temperature-fisher-river.xlsx')
daily_temp.head()

	Date	Mean_Temperature
0	1988-01-01	-23.0
1	1988-01-02	-20.5
2	1988-01-03	-22.0
3	1988-01-04	-30.5
4	1988-01-05	-31.0

• Hacemos que la fecha formateada sea el índice de la fila del conjunto de datos y elimine la columna Date

daily_temp.index = daily_temp['Date'].map(lambda date: pd.to_datetime(date, '%Y-%m-%d'))
daily_temp.drop('Date', axis=1, inplace=True)
daily_temp.head()

	Mean_Temperature
Date
1988-01-01	-23.0
1988-01-02	-20.5
1988-01-03	-22.0
1988-01-04	-30.5
1988-01-05	-31.0

fig = plt.figure(figsize=(5.5, 5.5))
ax = fig.add_subplot(1,1,1)
ax.set_title('Daily temperatures of Fisher River, TX, US');
daily_temp.plot(ax=ax);

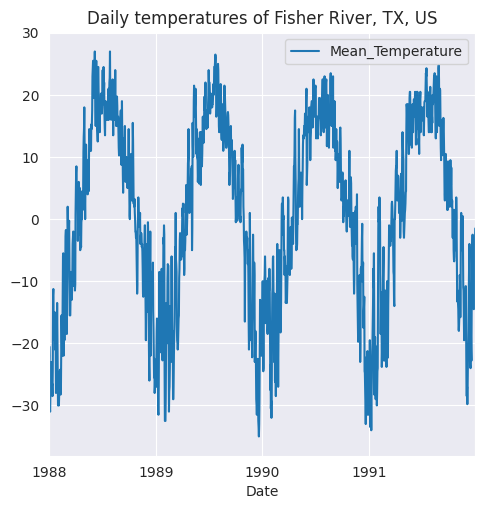
• Calculamos la temperatura media mensual

montly_resample = daily_temp['Mean_Temperature'].resample('M')
monthly_mean_temp = montly_resample.mean()
print('Shape of monthly mean temperature dataset:', monthly_mean_temp.shape)
monthly_mean_temp.head()

Shape of monthly mean temperature dataset: (48,)

Date
1988-01-31   -22.137097
1988-02-29   -19.025862
1988-03-31    -8.258065
1988-04-30     2.641667
1988-05-31    11.290323
Freq: ME, Name: Mean_Temperature, dtype: float64

• Trazamos la temperatura media mensual

fig = plt.figure(figsize=(5.5, 5.5))
ax = fig.add_subplot(1,1,1)
ax.set_title('Monthly mean temperatures of Fisher River, TX, US')
monthly_mean_temp.plot(ax=ax);

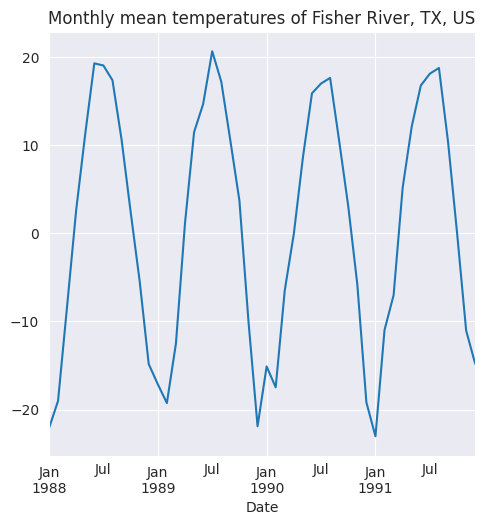
• Trazamos la ACF de la temperatura media mensual con pandas.tools.plotting.autocorrelation_plot

fig = plt.figure(figsize=(5.5, 5.5))
ax = fig.add_subplot(1,1,1)
ax.set_title('ACF of monthly mean temperatures of Fisher River, TX, US')
autocorrelation_plot(monthly_mean_temp, ax=ax);

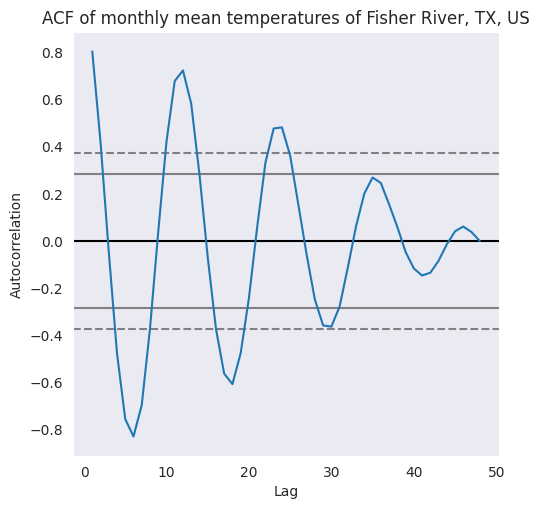
• Tomamos las diferencias estacionales con un periodo de 12 meses en las temperaturas medias mensuales. La diferenciación estacional deja valores nulos en sus primeros 12 elementos, que se eliminan antes del análisis:

seasonal_diff = monthly_mean_temp.diff(12)
seasonal_diff = seasonal_diff[12:]

• Trazamos las diferencias estacionales. Las diferencias estacionales parecen ser variaciones aleatorias, como se muestra en la siguiente figura

fig = plt.figure(figsize=(5.5, 5.5))
ax = fig.add_subplot(1,1,1)
ax.set_title('Seasonal differences');
seasonal_diff.plot(ax=ax);

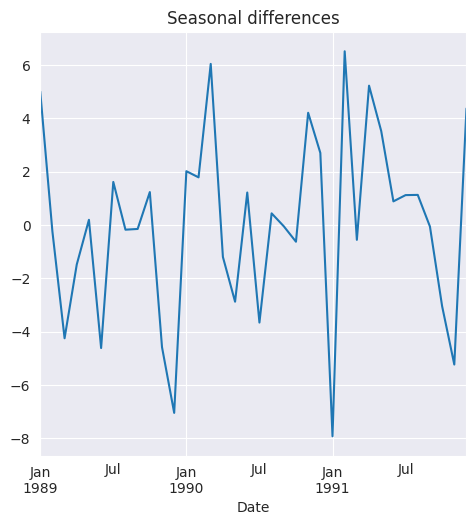
• Trazamos las diferencias estacionales. Volvemos a utilizar la función autocorrelation_plot para generar la ACF de la serie diferenciada y los intervalos de confianza al 99% del nivel de confianza. Podemos ver en la siguiente figura que la ACF nunca cruza los intervalos de confianza del 99% para rezagos que varían de 0 a más de 35

fig = plt.figure(figsize=(5.5, 5.5))
ax = fig.add_subplot(1,1,1)
ax.set_title('ACF of Seasonal differences');
autocorrelation_plot(seasonal_diff, ax=ax);

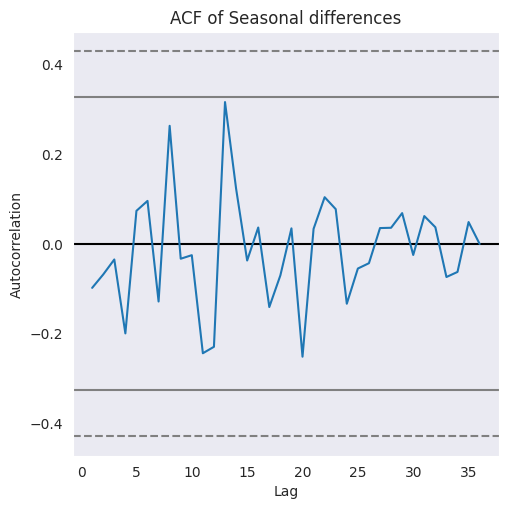
• Realizamos la prueba de Ljung-Box sobre la temperatura media mensual para obtener los valores \(p\). Utilizaremos rezagos de hasta 10. Los valores \(p\) reales se confirman ejecutando la función stattools.acf en los datos medios mensuales de la siguiente manera

_, _, _, pval_monthly_mean = stattools.acf(monthly_mean_temp,
                                           nlags=10, 
                                           qstat=True, 
                                           alpha=0.05)
print('Null hypothesis is rejected for lags:', np.where(pval_monthly_mean<=0.05))

Null hypothesis is rejected for lags: (array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]),)

• La prueba de Ljung-Box se realiza también con las series diferenciadas estacionalmente.

_, _, _, pval_seasonal_diff = stattools.acf(seasonal_diff,
                                            nlags=10, 
                                            qstat=True, 
                                            alpha=0.05)
print('Null hypothesis is rejected for lags:', np.where(pval_seasonal_diff<=0.05))

Null hypothesis is rejected for lags: (array([], dtype=int64),)

• No hay rezagos para los que se rechace la hipótesis nula de la prueba de Ljung-Box. La elección de una estrategia de diferenciación puede determinarse mediante un análisis exploratorio de los datos como los descritos hasta ahora. Sin embargo, cuando es difícil determinar qué transformaciones son necesarias para estacionar una serie de tiempo, se realiza la prueba ADF para una orientación

1.29. Prueba de Dickey-Fuller

• Dada una serie temporal generada por un proceso con una estructura Autorregresiva de Primer Orden, AR(1), también conocida como proceso de primer orden de Markov, y es ampliamente utilizada en diversas disciplinas

  (1.4)\[ y_{t}=\phi y_{t-1}+\varepsilon_{t}, \]

  donde \(\phi\) es un término de perturbación estacionario o coeficiente de autocorrelación, y \(\varepsilon_{t}\) es una variable aleatoria estacionaria e independiente.

• Si \(\phi=1\), la ecuación característica del proceso tiene una raíz unitaria, lo que indica que el proceso es no estacionario. Mientras \(\varepsilon_{t}\) sea estacionario, las primeras diferencias de \(y_{t}\) son estacionarias. La serie \(y_{t}\) es de integración de primer orden. Si \(\phi<1\), la serie temporal \(\phi_{t}\) es estacionaria en el sentido de que es una integración de orden cero.

• La prueba de DF [Dickey and Fuller, 1979] consiste en la hipótesis nula de que en un modelo, representado por la Ecuación (1.4) para \(\delta=\phi-1\) como sigue

  \[ \Delta y_{t}=\delta y_{t-1}+\varepsilon_{t}. \]

• En el caso de \(\delta=0\), la serie temporal \(y_{t}\) es un proceso browniano con acumulación de choques aleatorios. La hipótesis alternativa \(\delta<0\) implica que la variable es estacionaria. El estadístico de prueba se calcula como \(t=\hat{\delta}/\hat{\sigma}_{\delta}\), similar al estadístico \(t\) de Student, pero, con una distribución de probabilidad diferente. Para tomar una decisión, se necesita un valor crítico en un nivel de significancia elegido.

Observación

• Si el estadístico de prueba supera un valor crítico, entonces no se puede rechazar la hipótesis nula sobre la presencia de una raíz unitaria en una serie. Sin embargo, si el estadístico de prueba es menor que el valor crítico, entonces se rechaza la hipótesis nula a favor de la estacionariedad de la serie temporal.

• Apliquemos la prueba ADF para verificar la estacionariedad en los datos mensuales de millas de avión de US Airlines recogidos entre 1963 y 1970. Utilizaremos la función adfuller de la API statsmodels.tsa.stattools para realizar las pruebas

• Antes de ejecutar la prueba ADF, la serie de tiempo se carga en un pandas.DataFrame y como se muestra en la siguiente figura, es evidente que la serie temporal tiene una tendencia alcista, así como estacionalidad y, por lo tanto, no es estacionaria, lo que se verificará mediante la prueba ADF

air_miles = pd.read_csv('/home/lihkir/Data/us-airlines-monthly-aircraft-miles-flown.csv')
air_miles.index = air_miles.Month

print('Shape of the DataFrame:', air_miles.shape)
air_miles.head()

Shape of the DataFrame: (97, 2)

	Month	U.S. airlines: monthly aircraft miles flown (Millions) 1963 -1970
Month
1963-01	1963-01	6827.0
1963-02	1963-02	6178.0
1963-03	1963-03	7084.0
1963-04	1963-04	8162.0
1963-05	1963-05	8462.0

• Cambiemos el nombre de la segunda columna

air_miles.rename(columns={'U.S. airlines: monthly aircraft miles flown (Millions) 1963 -1970':\
                          'Air miles flown'}, inplace=True)

• Comprobamos si existen datos faltantes y eliminamos la fila correspondiente

missing = pd.isnull(air_miles['Air miles flown'])
print('Number of missing values found:', missing.sum())
air_miles = air_miles.loc[~missing, :]

Number of missing values found: 1

• Trazamos la serie temporal de millas aéreas voladas

fig = plt.figure(figsize=(5.5, 5.5))
ax = fig.add_subplot(1,1,1)
air_miles['Air miles flown'].plot(ax=ax)
ax.set_title('Monthly air miles flown during 1963 - 1970');

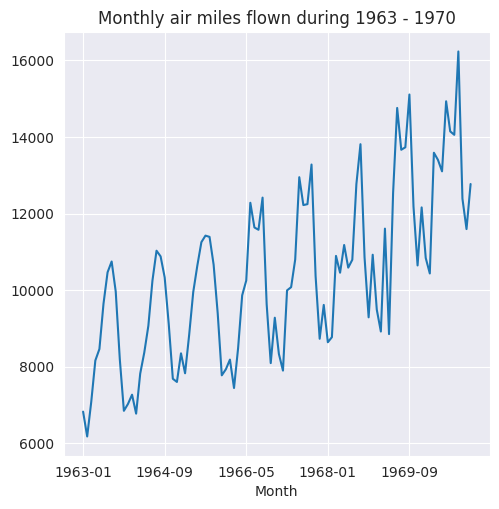
adf_result = stattools.adfuller(air_miles['Air miles flown'], autolag='AIC')

print('p-val of the ADF test in air miles flown:', adf_result[1])

p-val of the ADF test in air miles flown: 0.9945022811234028

• El argumento autolag='AIC' indica a la función que elija un número adecuado de rezagos para la prueba, maximizando el criterio de información de Akaike (AIC). Esto evita la necesidad de especificar manualmente el número de rezagos y reduce el proceso de prueba y error.

• El \(p\)-value de la prueba ADF es 0.9945, lo que confirma nuestros hallazgos del análisis exploratorio de datos. La función adfuller devuelve varios valores en una tupla. Hemos almacenado los resultados en la variable adf_resultado y accedido al segundo elemento adf_result[1] para obtener el \(p\)-value de la prueba.

• También se proporcionan otros datos interesantes, como el número de rezagos utilizados (usedlag) y los valores críticos del estadístico de prueba para diferentes niveles de confianza.

1.30. Descomposición de series temporales

• También existe un enfoque “clásico” para la descomposición de una serie de tiempo en componentes de tendencia y estacionales (de hecho, hay muchos algoritmos de descomposición diferentes; aquí explicamos un enfoque muy simple pero útil). El modelo matemático general para esta descomposición es

  \[ y_{t}=f(S_{t}, T_{t}, \varepsilon_{t}) \]

  donde \(S_{t}\) es el componente estacional, \(T_{t}\) es el efecto de la tendencia y \(\varepsilon_{t}\) es el componente de error aleatorio. Normalmente, hay dos formas para la función \(f\): un modelo aditivo

  \[ y_{t}=S_{t}+T_{t}+\varepsilon_{t} \]

  y un modelo multiplicativo

  \[ y_{t}=S_{t}T_{t}\varepsilon_{t}. \]

• El modelo aditivo es apropiado si la magnitud (amplitud) de la variación estacional no varía con el nivel de la serie, mientras que la versión multiplicativa es más apropiada si la amplitud de las fluctuaciones estacionales aumenta o disminuye con el nivel promedio de la serie temporal.

• La descomposición es útil para desglosar una serie temporal en estas partes componentes. Para el modelo aditivo, es relativamente fácil. Primero, modelaríamos y eliminaríamos la tendencia. Se podría utilizar un modelo lineal simple para hacer esto, por ejemplo,

\[ T_{t}=\beta_{0}+\beta_{1}t. \]

Observación

• Otros métodos también podrían ser utilizados. Los promedios móviles pueden ser utilizados para aislar una tendencia y eliminarla de los datos originales, al igual que métodos de regresión más sofisticados. Estas técnicas podrían ser apropiadas cuando la tendencia no es una línea recta a lo largo de la historia de la serie temporal. También se podría usar la diferenciación, aunque típicamente no se usa en el enfoque de descomposición clásico.

• Una vez estimado el componente de tendencia o ciclo de tendencia, la serie sin tendencia es

  \[ y_{t}-T_{t}=S_{t}+\varepsilon_{t}. \]

• Se calculan factores estacionales para cada período, como los meses, tomando un promedio de los efectos estacionales para cada período. Esto proporciona índices estacionales que representan la variación estacional para cada período. En la descomposición multiplicativa, se utilizan ratios para remover tendencia

  \[ \frac{y_{t}}{T_{t}}=S_{t}\varepsilon_{t}. \]

• Los índices estacionales se calculan tomando el promedio de todos los valores sin tendencia para cada período en la temporada.

• En esta sección, discutiremos los siguientes dos métodos populares para estimar la tendencia y los componentes estacionales:

  • Método de medias móviles

  • Descomposición estacional y de tendencia mediante la librería de Python statsmodels.tsa

1.31. Medias móviles y efectos de suavización

• Las medias móviles (MA) en un índice temporal \(t\) estiman el componente de ciclo de tendencia media \(M_{t}\) y se calcula sacando la media a lo largo del periodo de tiempo \(t\pm k\), donde \(k\) es el rango de la MA

\[\widehat{M}_{t}=\frac{y_{t-k}+y_{t-k+1}+\cdots+y_{t}+\cdots+y_{t+k-1}+y_{t+k}}{2k+1}\]

• La toma de medias móviles tiene el efecto de suavizar la serie temporal original eliminando el ruido aleatorio. Comúnmente, el número total de observaciones \(m = 2k + 1\) se utiliza para describir la media móvil como MA de orden \(m\), que en adelante se denotará como \(\widehat{M}_{t}^{(m)}\).

• El análisis de las medias móviles se ilustra utilizando el ejemplo de las cotizaciones de acciones de IBM de 1962 a 1965. La serie temporal original, representada en azul en el gráfico, muestra movimientos irregulares debido al ruido aleatorio. Por otro lado, la media móvil (MA) de 5 días, en rojo, es más suave que la serie original y ofrece una estimación del patrón de tendencia-ciclo. Se observa un efecto de suavización en la serie temporal original debido a la MA de 5 días, como se muestra en el gráfico.

import pandas as pd
from matplotlib import pyplot as plt

• Cargamos el conjunto de datos en un pandas.DataFrame

ibm_df = pd.read_csv('/home/lihkir/Data/ibm-common-stock-closing-prices.csv')
ibm_df.index = ibm_df['Date']

print('Shape of the dataframe:', ibm_df.shape)
ibm_df.head()

Shape of the dataframe: (1009, 2)

	Date	IBM common stock closing prices
Date
1962-01-02	1962-01-02	572.00
1962-01-03	1962-01-03	577.00
1962-01-04	1962-01-04	571.25
1962-01-05	1962-01-05	560.00
1962-01-08	1962-01-08	549.50

• Renombramos la segunda columna

ibm_df.rename(columns={'IBM common stock closing prices': 'Close_Price'}, inplace=True)
ibm_df.head()

	Date	Close_Price
Date
1962-01-02	1962-01-02	572.00
1962-01-03	1962-01-03	577.00
1962-01-04	1962-01-04	571.25
1962-01-05	1962-01-05	560.00
1962-01-08	1962-01-08	549.50

• Eliminamos datos faltantes

missing = (pd.isnull(ibm_df['Date'])) & (pd.isnull(ibm_df['Close_Price']))
print('No. of rows with missing values:', missing.sum())
ibm_df = ibm_df.loc[~missing, :]

No. of rows with missing values: 0

• Para ilustrar la idea de la media móvil, calculamos una media móvil semanal tomando una ventana de 5 días en lugar de 7, ya que el trading se produce solo durante los días laborables.

ibm_df['5-Day Moving Avg'] = ibm_df['Close_Price'].rolling(5).mean()

fig = plt.figure(figsize=(5.5, 5.5))
ax = fig.add_subplot(2,1,1)
ibm_df['Close_Price'].plot(ax=ax, color='b')
ax.set_title('IBM Common Stock Close Prices during 1962-1965')
ax = fig.add_subplot(2,1,2)
ibm_df['5-Day Moving Avg'].plot(ax=ax, color='r')
ax.set_title('5-day Moving Average')
plt.tight_layout(pad=0.4, w_pad=0.5, h_pad=2.0)

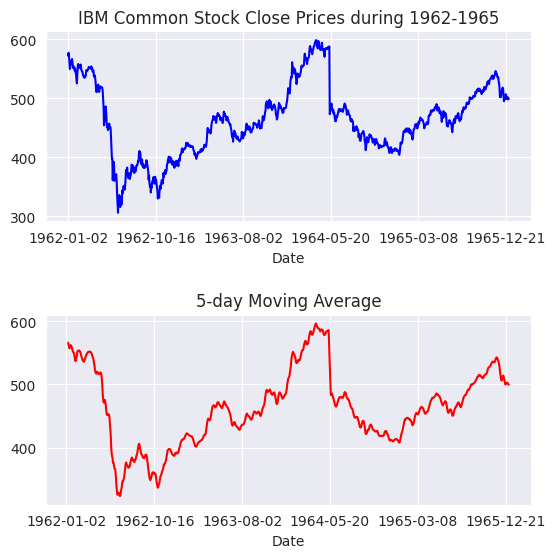
• La mencionada MA de orden impar \(m = 2\times2 + 1 = 5\) y es simétrica con igual número de observaciones a ambos lados del índice de tiempo \(t\) en el que se calcula la MA. Sin embargo, es posible tener una MA asimétrica de orden par \(m = 2k\).

• La asimetría de un promedio móvil de orden par puede ser eliminada tomando un segundo promedio móvil de igual orden. Ilustremos esto considerando el primer promedio móvil de orden dos y calculado como

  \[ \widehat{M}_{t}^{(2)}=\frac{y_{t-1}+y_{t}}{2} \]

• Otro promedio móvil de segundo orden, cuando es aplicado a la serie \(\widehat{M}_{t}^{(2)}\), producirá un promedio móvil final simétrico que tiene una observación a cada lado de la observación de la serie temporal original en el índice \(t\)

  \[ \overline{\widehat{M}_{t}^{(2)}}^{(t, t+1)}=\frac{\widehat{M}_{t}^{(2)}+\widehat{M}_{t+1}^{(2)}}{2}=\frac{1}{2}\left(\frac{y_{t-1}+y_{t}}{2}+\frac{y_{t}+y_{t+1}}{2}\right)=\frac{1}{4}y_{t-1}+\frac{1}{2}y_{t}+\frac{1}{4}y_{t+1}. \]

• Análogamente, dada la MA \(\widehat{M}_{t}^{(3)}=(y_{t-1}+y_{t}+y_{t+1})/3\), se tiene que (verifíquelo)

  \[\begin{split} \begin{align*} \overline{\widehat{M}_{t}^{(3)}}^{(t-1, t+1)} &= \frac{\widehat{M}_{t-1}^{(3)}+\widehat{M}_{t}^{(3)}+\widehat{M}_{t+1}^{(3)}}{3}=\frac{1}{9}y_{t-2}+\frac{2}{9}y_{t-1}+y_{t}+\frac{2}{9}y_{t+1}+\frac{1}{9}y_{t+2}\\ \overline{\widehat{M}_{t}^{(3)}}^{(t, t+1)} &= \frac{\widehat{M}_{t}^{(3)}+\widehat{M}_{t+1}^{(3)}}{2}=\frac{1}{6}y_{t-1}+\frac{1}{3}y_{t}+\frac{1}{3}y_{t+1}+\frac{1}{6}y_{t+2}. \end{align*} \end{split}\]

• El gráfico que se presenta aquí muestra seis medias móviles, a saber \(\widehat{M}_{t}^{(2)}\), \(\overline{\widehat{M}_{t}^{(2)}}^{(t,t+1)}\), \(\widehat{M}_{t}^{(4)}\), \(\overline{\widehat{M}_{t}^{(4)}}^{(t,t+1)}\), \(\widehat{M}_{t}^{(3)}\) y \(\overline{\widehat{M}_{t}^{(3)}}^{(t-1,t+1)}\) para los precios de las acciones de IBM hasta los primeros 45 días. Como se ilustra, la suavidad de los MA resultantes mejora con el aumento del orden \(m\) y el número de repeticiones \(n\).

• En la siguiente figura, las MA de tipo \(\widehat{M}_{t}^{(m)}\) se indican con líneas continuas, mientras que las del tipo \(\overline{\widehat{M}_{t}^{(m)}}^{(t-i, t+j)}, i,j\in\{0, 1, 2,\dots\}\) se representan con líneas discontinuas. Para generar las seis MA mencionadas hemos utilizado ampliamente las funciones rolling y mean

MA2 = ibm_df['Close_Price'].rolling(window=2).mean()
TwoXMA2 = MA2.rolling(window=2).mean()

MA4 = ibm_df['Close_Price'].rolling(window=4).mean()
TwoXMA4 = MA4.rolling(window=2).mean()

MA3 = ibm_df['Close_Price'].rolling(window=3).mean()
ThreeXMA3 = MA3.rolling(window=3).mean()

• Eliminemos los valores NaN de las variables anteriores

TwoXMA2 = MA2.dropna()
TwoXMA4 = MA4.dropna()
ThreeXMA3 = MA3.dropna()

f, axarr = plt.subplots(3, sharex=True)
f.set_size_inches(5.5, 6.5)

ibm_df['Close_Price'].iloc[:45].plot(color='b', linestyle = '-', ax=axarr[0])
MA2.iloc[:45].plot(color='r', linestyle = '--', ax=axarr[0])
TwoXMA2.iloc[:45].plot(color='g', linestyle = '--', ax=axarr[0])
axarr[0].set_title('2 day MA & 2X2 day MA');

ibm_df['Close_Price'].iloc[:45].plot(color='b', linestyle = '-', ax=axarr[1])
MA4.iloc[:45].plot(color='r', linestyle = '--', ax=axarr[1])
TwoXMA4.iloc[:45].plot(color='g', linestyle = '--', ax=axarr[1])
axarr[1].set_title('4 day MA & 2X4 day MA');

ibm_df['Close_Price'].iloc[:45].plot(color='b', linestyle = '-', ax=axarr[2])
MA3.iloc[:45].plot(color='r', linestyle = '--', ax=axarr[2])
ThreeXMA3.iloc[:45].plot(color='g', linestyle = '--', ax=axarr[2])
axarr[2].set_title('3 day MA & 3X 3day MA');

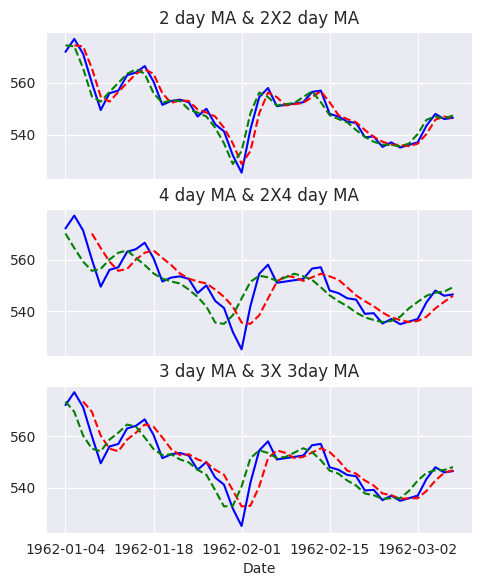
1.32. Ajuste estacional mediante media móvil

• La propiedad de media ponderada de las \(\overline{\widehat{M}_{t}^{(m)}}^{(t-i, t+j)}\hspace{-6mm},i,j\in\{0,1,2,\dots\}\) medias móviles tiene aplicación en suavizar datos con estacionalidad para generar estimaciones de ciclos de tendencia. Por ejemplo, dadas las observaciones trimestrales podemos aplicar la MA: \(\overline{\widehat{M}_{t}^{(4)}}^{(t, t+1)}\) para suavizar los datos.

• El enfoque de utilizar MA ponderado de la forma \(\overline{\widehat{M}_{t}^{(4)}}^{(t, t+1)}\) se ilustra utilizando los datos de producción de cerveza de Australia. La serie temporal representa la producción trimestral de cerveza desde marzo de 1956 a junio de 1994. La serie temporal original y una serie de MA \(\overline{\widehat{M}_{t}^{(4)}}^{(t, t+1)}\) son dibujadas.

import pandas as pd
from matplotlib import pyplot as plt

beer_df = pd.read_csv('/home/lihkir/Data/quarterly-beer-production-in-aus-March 1956-June 1994.csv')
beer_df.index = beer_df['Quarter']

print('Shape of the dataframe:', beer_df.shape)
beer_df.head()

Shape of the dataframe: (154, 2)

	Quarter	Quarterly beer production in Australia: megalitres. March 1956 ? June 1994
Quarter
1956Q1	1956Q1	284.4
1956Q2	1956Q2	212.8
1956Q3	1956Q3	226.9
1956Q4	1956Q4	308.4
1957Q1	1957Q1	262.0

• Renombramos la segunda columna del pandas.DataFrame

beer_df.rename(columns={'Quarterly beer production in Australia: megalitres. March 1956 ? June 1994':'Beer_Prod'},
               inplace=True)

• Eliminamos datos faltantes NaNs

missing = (pd.isnull(beer_df['Quarter'])) | (pd.isnull(beer_df['Beer_Prod']))
print('Number of rows with at least one missing values:', missing.sum())
beer_df = beer_df.loc[~missing, :]
print('Shape after removing missing values:', beer_df.shape)

Number of rows with at least one missing values: 0
Shape after removing missing values: (154, 2)

• Para eliminar los patrones estacionales, calculemos la media móvil trimestral \(\overline{\widehat{M}_{t}^{(4)}}^{(t, t+1)}\)

MA4 = beer_df['Beer_Prod'].rolling(window=4).mean()
TwoXMA4 = MA4.rolling(window=2).mean()
TwoXMA4 = TwoXMA4.loc[~pd.isnull(TwoXMA4)]

• Trazamos la serie temporal original y las medias móviles estacionales

fig = plt.figure(figsize=(5.5, 5.5))
ax = fig.add_subplot(1,1,1)
beer_df['Beer_Prod'].plot(ax=ax, color='b', linestyle='-')
TwoXMA4.plot(ax=ax, color='r', linestyle='-')
plt.xticks(rotation=60);
ax.set_title('Quaterly Beer Production between in Australia and 2X4 quarter MA');

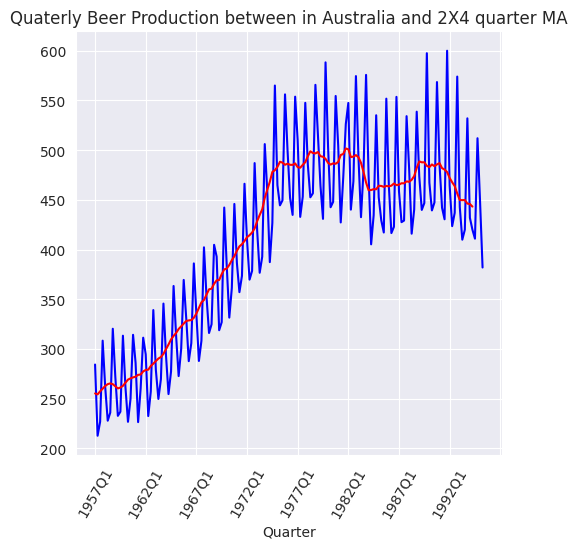
• La serie de producción trimestral de cerveza muestra tanto tendencia como estacionalidad, lo que la hace no estacionaria. Para abordar esto, primero eliminamos el componente de tendencia y luego consideramos las diferencias estacionales. Los residuos resultantes después de eliminar la tendencia se muestran en la siguiente figura.

residuals = beer_df['Beer_Prod']-TwoXMA4
residuals = residuals.loc[~pd.isnull(residuals)]

fig = plt.figure(figsize=(5.5, 5.5))
ax = fig.add_subplot(1,1,1)
residuals.plot(ax=ax, color='b', linestyle='-')
plt.xticks(rotation=60);
ax.set_title('Residuals in Quaterly Beer Production time series');

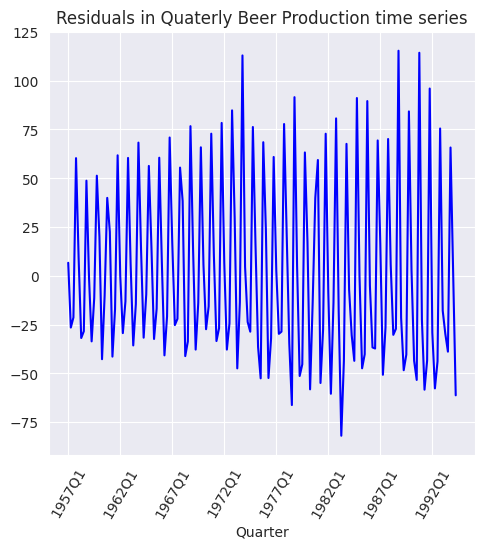
• En este punto comprobaremos si los residuos ya están estacionados (aunque poco probable) trazando la función de autocorrelación junto con los intervalos de confianza del 99%. Para obtener este gráfico, que se muestra aquí, utilizaremos la función autocorrelation_plot de la API pandas.plotting

from pandas.plotting import autocorrelation_plot

fig = plt.figure(figsize=(5.5, 5.5))
ax = fig.add_subplot(1,1,1)
autocorrelation_plot(residuals, ax=ax)
ax.set_title('ACF of Residuals in Quaterly Beer Production time series');
autocorrelation_plot(residuals);

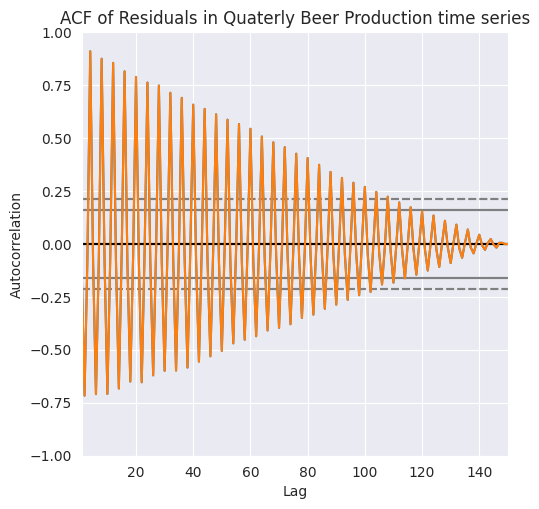
• Los residuos exhiben una autocorrelación significativa, como se evidencia en el ACF, con varios rezagos superando los intervalos de confianza. Por lo tanto, debemos aplicar diferencias estacionales en los residuos. Dado que los datos originales abarcan todos los trimestres de varios años, y muestran estacionalidad trimestral, optamos por diferencias a lo largo de periodos de cuatro unidades de tiempo más transformación logarítmica. Verifique que pasa si se omite la transformación np.log()

residuals_qtr_diff = np.log(residuals.diff(4))

• Removemos todos los valores faltantes NaNs

residuals_qtr_diff = residuals_qtr_diff.loc[~pd.isnull(residuals_qtr_diff)]

• residuals_qtr_diff parece representar fluctuaciones aleatorias sin patrones estacionales ni autocorrelación notable. Al trazar la autocorrelación de residuals_qtr_diff, observamos una ACF principalmente aleatoria. Esto sugiere que las diferencias estacionales han logrado estacionar los residuos.

fig = plt.figure(figsize=(5.5, 5.5))
ax = fig.add_subplot(1,1,1)
autocorrelation_plot(residuals_qtr_diff, ax=ax)
ax.set_title('ACF of Quaterly Differenced Residuals');

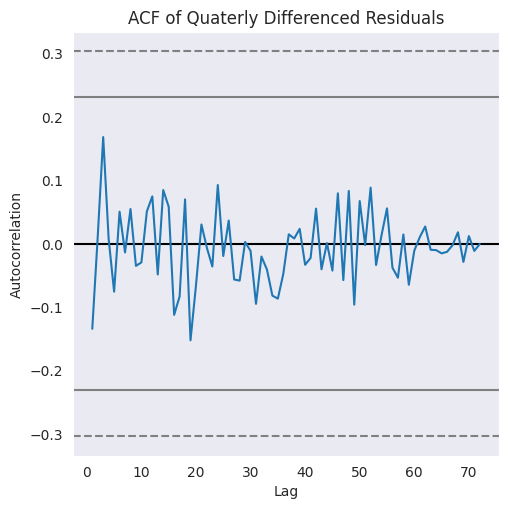
_, _, _, pval_monthly_mean = stattools.acf(residuals_qtr_diff,
                                           nlags=10, 
                                           qstat=True, 
                                           alpha=0.05)
print('Null hypothesis is rejected for lags:', np.where(pval_monthly_mean<=0.05))

Null hypothesis is rejected for lags: (array([], dtype=int64),)

• Nuestro enfoque para estacionar la serie temporal de producción de cerveza trimestral puede ser resumir como sigue:

  1. Tomar estacionalidad MA \(\overline{\widehat{M}_{t}^{(4)}}^{(t, t+1)}\)

  2. Calcule los residuos, restando \(y_{t}\) de la MA \(\overline{\widehat{M}_{t}^{(4)}}^{(t, t+1)}\) de la serie de tiempo original

  3. Comprobar aleatoriedad/independencia de la ACF de los residuos

  4. Si el ACF de los residuos ya es aleatorio/independiente, entonces los residuos son estacionarios, si no pase a la etapa siguiente.

  5. Tome diferencias estacionales en los residuos con periodicidad de cuatro y compruebe la aleatoriedad de la ACF de la serie diferenciada.

• Por lo tanto, las medias móviles estacionales y las diferencias estacionales en los residuos han estacionado la serie temporal original.

1.33. Media móvil ponderada

• En la sección anterior, expresamos las medias móviles de la forma \(\overline{\widehat{M}_{t}^{(4)}}^{(t-i, t+j)}\) como suma ponderada de las observaciones de la serie temporal original. Vimos cómo las ponderaciones caen para observaciones alejadas del índice temporal en el que se calcula la MA. La noción de medias móviles ponderadas, que es simétrica, puede generalizarse para cualquier aplicación de la siguiente manera:

  \[\widehat{W}_{t}^{(k)}=w_{t-k}y_{t-k}+w_{t-k+1}y_{t-k+1}+\cdots+w_{t}y_{t}+\cdots+w_{t+k-1}y_{t+k-1}+w_{t+k}y_{t+k},\]

  donde los pesos \(w_{t-k}+w_{t-k+1}+\cdots+w_{t-k-1}+w_{t+k}=1\). Las observaciones cercanas al índice de tiempo \(t\) se les asigna una mayor ponderación, mientras que las más alejadas reciben una ponderación menor.

• Para un simple MA \(\widehat{W}_{t}^{(k)}\) los pesos son \(1/N,~N\in\mathbb{Z}^{+}\). Se ha observado que el MA ponderado produce una estimación más suave del ciclo de la tendencia. Esto se atribuye al hecho de que todas las observaciones de la serie temporal original, que se utilizan para calcular el MA ponderado, no se ponderan usando el mismo peso como en el caso de una MA \(\widehat{M}_{t}^{(k)}\).

1.34. Descomposición de series temporales mediante medias móviles

• Las medias móviles se utilizan para suavizar la serie original y estimar el componente de ciclo de la tendencia. La elección de los parámetros es crucial, siendo la periodicidad de los datos un factor determinante. En el caso de una periodicidad par, se ajusta para obtener una mejor estimación. La estimación del componente estacional se genera a partir de la media estacional de los residuos. Los cálculos difieren entre modelos aditivos y multiplicativos.

• Finalmente, las variaciones irregulares se obtienen mediante ajustes adicionales de la serie original. Se ilustra este enfoque con la serie temporal de los kilómetros mensuales de las aeronaves voladas por US Airlines, aplicando modelos aditivos y multiplicativos

import pandas as pd
import numpy as np
from statsmodels.tsa import stattools
from matplotlib import pyplot as plt

air_miles = pd.read_csv('/home/lihkir/Data/us-airlines-monthly-aircraft-miles-flown.csv')
air_miles.index = air_miles['Month']

print('Shape of the DataFrame:', air_miles.shape)
air_miles.head()

Shape of the DataFrame: (97, 2)

	Month	U.S. airlines: monthly aircraft miles flown (Millions) 1963 -1970
Month
1963-01	1963-01	6827.0
1963-02	1963-02	6178.0
1963-03	1963-03	7084.0
1963-04	1963-04	8162.0
1963-05	1963-05	8462.0

• Cambiemos el nombre de la segunda columna

air_miles.rename(columns={'U.S. airlines: monthly aircraft miles flown (Millions) 1963 -1970': 'Air miles flown'}, 
                 inplace=True)
air_miles.head()

	Month	Air miles flown
Month
1963-01	1963-01	6827.0
1963-02	1963-02	6178.0
1963-03	1963-03	7084.0
1963-04	1963-04	8162.0
1963-05	1963-05	8462.0

• Comprobar si existen datos faltantes y los eliminamos

missing = pd.isnull(air_miles['Air miles flown'])
print('Number of missing values found:', missing.sum())
air_miles = air_miles.loc[~missing, :]

Number of missing values found: 1

• Estimamos el componente de tendencia mediante la media móvil mensual 2X12

MA12 = air_miles['Air miles flown'].rolling(window=12).mean()
trendComp = MA12.rolling(window=2).mean()

• Para el modelo aditivo, el componente estacional se obtiene restando la tendencia-ciclo de la serie temporal original y tomando las medias mensuales de los residuos. La operación de agrupación para calcular el componente estacional de la siguiente manera

residuals = air_miles['Air miles flown'] - trendComp

month = air_miles['Month'].map(lambda d: d[-2:])
monthwise_avg = residuals.groupby(by=month).aggregate(['mean'])
nb_years = 1970-1963+1

seasonalComp = np.array([monthwise_avg.values]*nb_years).reshape((12*nb_years,))

• Dadas las estimaciones de los componentes de tendencia-ciclo y estacional, obtenemos las variaciones irregulares como sigue para un modelo aditivo

irr_var = air_miles['Air miles flown'] - trendComp - seasonalComp

• La serie temporal original, los componentes de tendencia-ciclo, estacional e irregular se muestran en la siguiente figura

fig, axarr = plt.subplots(4, sharex=True)
fig.set_size_inches(5.5, 5.5)

air_miles['Air miles flown'].plot(ax=axarr[0], color='b', linestyle='-')
axarr[0].set_title('Monthly air miles')

pd.Series(data=trendComp, index=air_miles.index).plot(ax=axarr[1], color='r', linestyle='-')
axarr[1].set_title('Trend component in monthly air miles')

pd.Series(data=seasonalComp, index=air_miles.index).plot(ax=axarr[2], color='g', linestyle='-')
axarr[2].set_title('Seasonal component in monthly air miles')

pd.Series(data=irr_var, index=air_miles.index).plot(ax=axarr[3], color='k', linestyle='-')
axarr[3].set_title('Irregular variations in monthly air miles')

plt.tight_layout(pad=0.4, w_pad=0.5, h_pad=2.0)

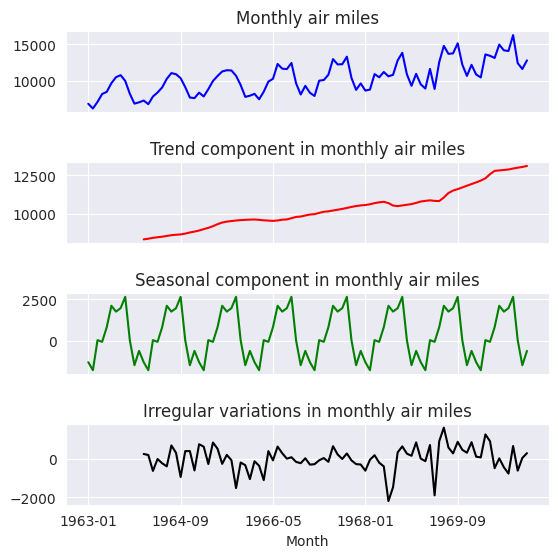
• La prueba ADF de irr_var da un valor \(p\) de 0.0658. Con un nivel de confianza del 90% (\(\alpha\)=0.10) la hipótesis nula sobre la no estacionariedad de las variaciones irregulares puede aceptarse. Sin embargo, vamos a intentar mejorar aún más mediante el modelo multiplicativo.

adf_result = stattools.adfuller(irr_var.loc[~pd.isnull(irr_var)], autolag='AIC')
print('p-val of the ADF test on irregular variations in air miles flown:', adf_result[1])

p-val of the ADF test on irregular variations in air miles flown: 0.06577411025730062

• La estimación del ciclo de la tendencia mediante MA es aplicable incluso para el modelo multiplicativo. Sin embargo, el cálculo del componente estacional cambia

residuals = air_miles['Air miles flown'] / trendComp

• Obsérvese que los residuos estacionales residuals dividen el componente de tendencia-ciclo de la serie temporal original en el caso de un modelo multiplicativo. Sin embargo, la operación de agrupación en los residuos sigue siendo la misma

month = air_miles['Month'].map(lambda d: d[-2:])
monthwise_avg = residuals.groupby(by=month).aggregate(['mean'])
nb_years = 1970-1963+1

seasonalComp = np.array([monthwise_avg.values]*nb_years).reshape((12*nb_years,))

• Finalmente, llegamos a las variaciones irregulares para el modelo multiplicativo como sigue

irr_var = air_miles['Air miles flown'] / (trendComp * seasonalComp)

• Obsérvese que los componentes estacionales e irregulares son de menor magnitud que los obtenidos con el modelo aditivo

fig, axarr = plt.subplots(4, sharex=True)
fig.set_size_inches(5.5, 5.5)

air_miles['Air miles flown'].plot(ax=axarr[0], color='b', linestyle='-')
axarr[0].set_title('Monthly air miles')

pd.Series(data=trendComp, index=air_miles.index).plot(ax=axarr[1], color='r', linestyle='-')
axarr[1].set_title('Trend component in monthly air miles')

pd.Series(data=seasonalComp, index=air_miles.index).plot(ax=axarr[2], color='g', linestyle='-')
axarr[2].set_title('Seasonal component in monthly air miles')

pd.Series(data=irr_var, index=air_miles.index).plot(ax=axarr[3], color='k', linestyle='-')
axarr[3].set_title('Irregular variations in monthly air miles')

plt.tight_layout(pad=0.4, w_pad=0.5, h_pad=2.0)

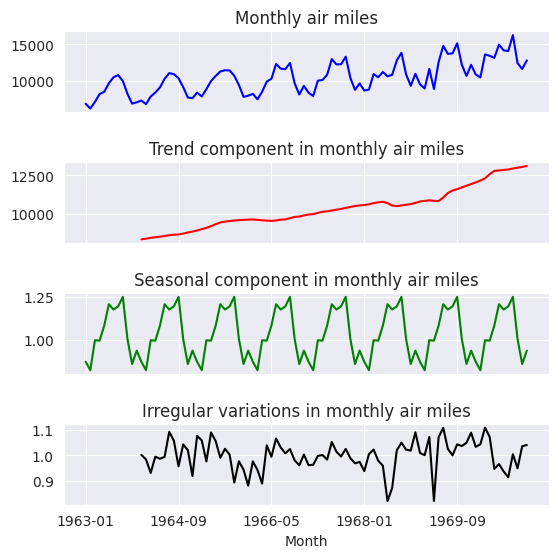
• La prueba ADF sobre las variaciones irregulares obtenida del modelo multiplicativo da un valor \(p\) de aproximadamente 0.00018, que es mucho menor que el obtenido con el modelo aditivo. Sobre todo, menor que el nivel de significancia del 0.01.

adf_result = stattools.adfuller(irr_var.loc[~pd.isnull(irr_var)], autolag='AIC')
print('p-val of the ADF test on irregular variations in air miles flown:', adf_result[1])

p-val of the ADF test on irregular variations in air miles flown: 0.00017645280908370881

1.35. Descomposición de series temporales mediante statsmodels.tsa

• Analizamos el uso de MA para estimar tendencias y estacionalidad en series temporales. Sin embargo, para patrones más complejos, como cambios en la estacionalidad, recurrimos al método STL [Cleveland et al., 1990] en que se usa Regresión Local (LOESS) en el proceso de suavización. En esta sección, emplearemos statsmodels.tsa en Python para estimar tendencias, ciclos y estacionalidad, luego aplicaremos la prueba ADF para verificar la estacionariedad de los datos.

• Consideremos la serie temporal del empleo mensual en Wisconsin, Estados Unidos, para ilustrar el enfoque antes mencionado. Los datos corresponden al periodo comprendido entre enero de 1961 y octubre de 1975. Comenzamos cargando el conjunto de datos en un pandas.DataFrame wisc_emp y ejecutando la prueba ADF para la serie temporal original como sigue

import pandas as pd
import numpy as np
from statsmodels.tsa import stattools
from statsmodels.tsa import seasonal
from matplotlib import pyplot as plt

wisc_emp = pd.read_csv('/home/lihkir/Data/wisconsin-employment-time-series.csv')
wisc_emp.index = wisc_emp['Month']

print('Shape of the DataFrame:', wisc_emp.shape)
wisc_emp.head(10)

Shape of the DataFrame: (178, 2)

	Month	Employment
Month
1961-01	1961-01	239.6
1961-02	1961-02	236.4
1961-03	1961-03	236.8
1961-04	1961-04	241.5
1961-05	1961-05	243.7
1961-06	1961-06	246.1
1961-07	1961-07	244.1
1961-08	1961-08	244.2
1961-09	1961-09	244.8
1961-10	1961-10	246.6

missing = (pd.isnull(wisc_emp['Employment'])) | (pd.isnull(wisc_emp['Month']))
print('Number of missing values found:', missing.sum())
wisc_emp = wisc_emp.loc[~missing, :]

Number of missing values found: 0

adf_result = stattools.adfuller(wisc_emp['Employment'], autolag='AIC')
print('p-val of the ADF test on irregular variations in employment data:', adf_result[1])

p-val of the ADF test on irregular variations in employment data: 0.9810000189539195

• Un valor \(p\) elevado de 0.9810 para la prueba ADF de la serie mensual de empleo indica que la serie temporal original es no estacionaria. Por lo tanto, intentamos descomponer la serie temporal y, en consecuencia, estacionarla utilizando la función seasonal.seasonal_decompose de la librería statsmodels.tsa. Intentemos primero el modelo aditivo para la descomposición

decompose_model = seasonal.seasonal_decompose(wisc_emp.Employment.tolist(), period=12, model='additive')

• El argumento period en el seasonal.seasonal_decompose es la periodicidad del comportamiento estacional y la serie temporal original, al ser observaciones mensuales, sospechamos una periodicidad de 12, que puede verificarse mediante un análisis exploratorio de los datos.

• Los componentes de tendencia-ciclo, estacional y residual de la serie temporal descompuesta son accesibles a través de los atributos del objeto decompose_model devuelto por el seasonal.seasonal_decompose. Estos componentes se pueden obtener a partir de los siguientes atributos de decompose_model:

  • decompose_model.trend: Componente de ciclo de tendencia

  • decompose_model.seasonal: Componente estacional

  • decompose_model.resid: Variaciones irregulares

fig, axarr = plt.subplots(4, sharex=True)
fig.set_size_inches(5.5, 5.5)

wisc_emp['Employment'].plot(ax=axarr[0], color='b', linestyle='-')
axarr[0].set_title('Monthly Employment')

pd.Series(data=decompose_model.trend, index=wisc_emp.index).plot(color='r', linestyle='-', ax=axarr[1])
axarr[1].set_title('Trend component in monthly employment')

pd.Series(data=decompose_model.seasonal, index=wisc_emp.index).plot(color='g', linestyle='-', ax=axarr[2])
axarr[2].set_title('Seasonal component in monthly employment')

pd.Series(data=decompose_model.resid, index=wisc_emp.index).plot(color='k', linestyle='-', ax=axarr[3])
axarr[3].set_title('Irregular variations in monthly employment')

plt.tight_layout(pad=0.4, w_pad=0.5, h_pad=2.0);
plt.xticks(rotation=10);

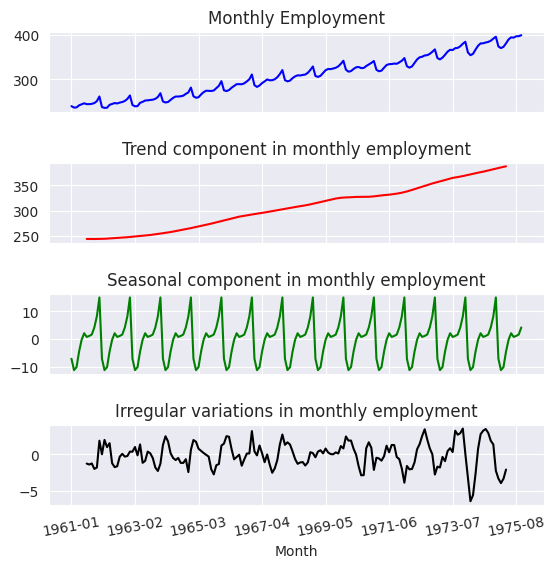
• Ahora ejecutamos la prueba ADF sobre los residuos del modelo aditivo y obtenemos un valor \(p\) de 0.00656, que es mucho menor que el obtenido con la serie temporal original. Sin embargo, construiremos también un modelo multiplicativo

adf_result = stattools.adfuller(decompose_model.resid[np.where(np.isfinite(decompose_model.resid))[0]], 
                                autolag='AIC')
print('p-val of the ADF test on irregular variations in employment data:', adf_result[1])

p-val of the ADF test on irregular variations in employment data: 0.006560931634642831

decompose_model = seasonal.seasonal_decompose(wisc_emp.Employment.tolist(), period=12, model='multiplicative')

fig, axarr = plt.subplots(4, sharex=True)
fig.set_size_inches(5.5, 5.5)

wisc_emp['Employment'].plot(ax=axarr[0], color='b', linestyle='-')
axarr[0].set_title('Monthly Employment');

axarr[1].plot(decompose_model.trend, color='r', linestyle='-')
axarr[1].set_title('Trend component in monthly employment');

axarr[2].plot(decompose_model.seasonal, color='g', linestyle='-')
axarr[2].set_title('Seasonal component in monthly employment');

axarr[3].plot(decompose_model.resid, color='k', linestyle='-')
axarr[3].set_title('Irregular variations in monthly employment');

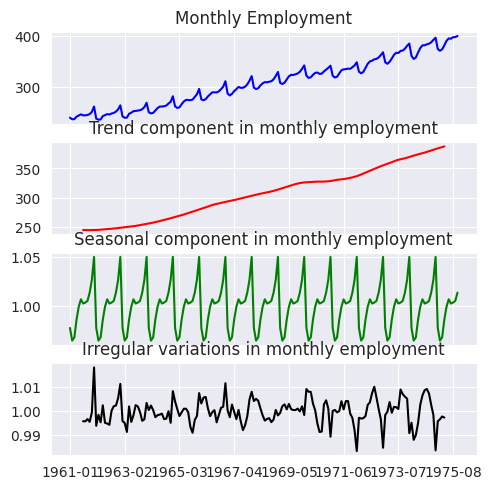
• La prueba ADF sobre los residuos de la descomposición multiplicativa da un valor \(p\) de 0.00123 que es incluso menor que el obtenido con la descomposición aditiva. Con un nivel de confianza del 99% (\(\alpha\)=0.01) podemos rechazar la hipótesis nula de la prueba ADF y concluir que los residuos del modelo de descomposición multiplicativa corresponden a una serie estacionaria

adf_result = stattools.adfuller(decompose_model.resid[np.where(np.isfinite(decompose_model.resid))[0]], 
                                autolag='AIC')
print('p-val of the ADF test on irregular variations in employment data:', adf_result[1])

p-val of the ADF test on irregular variations in employment data: 0.0012347837267736395

1.36. Residual y error de predicción

Definition 1.4

• Supongamos que se dispone de \(T\) periodos de datos disponibles, siendo el periodo \(T\) el más reciente. Denotemos por \(y_{t}\) la observación de esta variable en el periodo de tiempo \(t,~t = 1,2,\dots, T\).

• En general, tendremos que distinguir entre una predicción o valor predicho de \(y_{t}\) que se hizo en algún periodo de tiempo previo, digamos, \(t-\tau\) y un valor ajustado de \(y_{t}\) que ha resultado de la estimación de los parámetros de un modelo de series temporales a datos históricos. Tenga en cuenta que \(\tau\) es el horizonte de predicción.

• La predicción realizada en el periodo de tiempo \(t-\tau\) se denota por \(\hat{y}_{t}(t-\tau)\). Hay mucho interés en la predicción basada en el tiempo previo \(\text{lead}-1\), que es la predicción de la observación en el periodo \(t\), \(y_{t}\), realizada un periodo previo, \(\hat{y}_{t}(t - 1)\).

• Denotaremos el valor ajustado de \(y_{t}\) por \(\hat{y}_{t}\). También nos interesará analizar los errores de predicción. El error de predicción que resulta de una predicción de \(y_{t}\) que se realizó en el periodo de tiempo \(t-\tau\) es el error de predicción \(\text{lead} - \tau\)

  \[\begin{split} \\[2mm] e_{t}(\tau)=y_{t}-\hat{y}_{t}(t-\tau). \end{split}\]

  Por ejemplo, el error de predicción \(\text{lead} - 1\) es

\[ e_{t}(1)=y_{t}-\hat{y}_{t}(t-1). \]

• La diferencia entre la observación \(y_{t}\) y el valor obtenido ajustando un modelo de series temporales a los datos, o un valor ajustado \(\hat{y}_{t}\) definido anteriormente, se denomina residual, y se denota por

\[ e_{t}=y_{t}-\hat{y}_{t}. \]

Observación

• La razón de esta cuidadosa distinción entre error de predicción y residual es que los modelos suelen ajustarse mejor a los datos históricos de lo que pronostican.

• Es decir, los residuos de un proceso de ajuste de modelo casi siempre serán menores que los errores de predicción que se experimentan cuando ese modelo se utiliza para pronosticar observaciones futuras.

1.37. Evaluando y monitoreando el desempeño del modelo predictivo

Introducción

• El desempeño o rendimiento de un modelo predictivo está relacionado con el ajuste del pronóstico o modelo de series temporales a datos historicos. Los usuarios de un modelo predictivo están siempre interesados la precisión de futuras predicciones, no en la bondad de ajuste del modelo, por lo tanto, es importante evaluar este aspecto de cualquier modelo recomendado

• En algunos casos, la precisión de predicción es llamada error de predicción “out of sample”, para distinguir esta del residual que proviene del proceso de ajuste del modelo. Cuando mas de una técnica predictiva parece razonable para una aplicación en particular, estas medidas de precisión del pronóstico pueden ser usadas para discriminar entre modelos que compiten entre ellos.

Rendimiento del modelo predictivo

• Es habitual evaluar el rendimiento de un modelo usando el error de pronóstico one-step-ahead

  \[ e_{t}(1)=y_{t}-\hat{y}_{t}(t-1) \]

  donde \(\hat{y}_{t}(t-1)\) es la predicción de \(y_{t}\) que fue hecha en el periodo previo. Errores de pronósticos en otros rezagos (lags), si está interesado en estos pronósticos particulares.

• Suponga que hay \(n\) observaciones para las cuales pronósticos han sido realizados y \(n\) errores one-step-ahead, \(e_{t}(1),~t=1,2,\dots, n\). Medidas estándar de precisión del pronóstico son el error promedio o error medio

  \[ \text{ME}=\frac{1}{n}\sum_{t=1}^{n}e_{t}(1), \]

  la desviación media absoluta (o error absoluto medio)

  \[ \text{MAD}=\frac{1}{n}\sum_{t=1}^{n}|e_{t}(1)|, \]

  y el error cuadrático medio

  \[ \text{MSE}=\frac{1}{n}\sum_{t=1}^{n}[e_{t}(1)]^{2} \]

• Claramente, queremos que la variabilidad del error de pronóstico sea pequeña. El MSE es un estimador directo de la varianza del error de predicción one-step-ahead

  \[ \hat{\sigma}_{e(1)}^{2}=\text{MSE}=\frac{1}{n}\sum_{t=1}^{n}[e_{t}(1)]^{2}. \]

• Si los errores de predicción están normalmente distribuidos, el MAD es relacionado con la desviación estándar de los errores de predicción por

  \[ \hat{\sigma}_{e(1)}=\sqrt{\frac{\pi}{2}}\text{MAD}\approx 1.25\text{MAD}. \]

• Además, las medidas de precisión que son dependientes de la escala no facilitan comparaciones de una técnica predictiva a través de diferentes series de tiempo, o comparación a través de diferentes periodos de tiempo. Para solucionar esto, definimos el error de predicción relativo (en porcentaje) como

  \[ re_{t}(1)=\left(\frac{y_{t}-\hat{y}_{t}(t-1)}{y_{t}}\right)100=\left(\frac{e_{t}(1)}{y_{t}}\right)100. \]

• La anterior métrica es llamada el error de pronóstico porcentual. La media del error de pronóstico porcentual (MPE) es

  \[ \text{MPE}=\frac{1}{n}\sum_{t=1}^{n}re_{t}(1) \]

  y la media absoluta del error de pronóstico porcentual (MAPE) es

  \[ \text{MAPE}=\frac{1}{n}\sum_{t=1}^{n}|re_{t}(1)|. \]

• Nótese que el error de pronóstico porcentual relativo solo tiene sentido si la serie de tiempo \(y_{t}\) no tiene valores nulos.

• Si una serie temporal es ruido blanco, la distribución del coeficiente de autocorrelación muestral en el rezago \(k\) en muestras grandes es aproximadamente normal con media cero y varianza \(1/T\); es decir,

  \[ r_{k}\sim N\left(0, \frac{1}{T}\right). \]

• Por lo tanto, podríamos probar la hipótesis \(H_{0}:~\rho_{k} = 0\) utilizando el estadístico de prueba

  (1.5)\[ Z_{0}=\frac{r_{k}}{\sqrt{1/T}}=r_{k}\sqrt{T}. \]

• Este procedimiento es una prueba one-at-a-time; es decir, el nivel de significancia se aplica a las autocorrelaciones consideradas individualmente. A menudo, estamos interesados en evaluar un conjunto de autocorrelaciones conjuntamente para determinar si indican que la serie temporal es ruido blanco. [Box and Pierce, 1970] han sugerido dicho procedimiento.

Box-Pierce test

• Considera el cuadrado del estadístico de prueba \(Z_{0}\) en la Ecuación (1.5). La distribución de \(Z_{0}^{2} = r_{k}^{2}T\) es aproximadamente chi-cuadrado con un grado de libertad. El estadístico de Box-Pierce

  \[ Q_{BP}=T\sum_{k=1}^{K}r_{k}^{2} \]

  bajo la hipótesis nula de que la serie temporal es ruido blanco, tiene una distribución chi-cuadrado aproximada con \(K\) grados de libertad. Por lo tanto, si \(Q_{BP} > \chi_{\alpha, K}^{2}\), rechazaríamos la hipótesis nula y concluiríamos que la serie temporal no es ruido blanco porque algunas de las autocorrelaciones no son cero.

• Una modificación de esta prueba que funciona mejor para muestras pequeñas fue ideada por [Ljung and Box, 1978]. El estadístico de bondad de ajuste de Ljung-Box es

  \[ Q_{LB}=T(T+2)\sum_{k=1}^{K}\left(\frac{1}{T-k}\right)r_{k}^{2}. \]

• Es importante destacar que el estadístico de bondad de ajuste de Ljung-Box es muy similar a la estadística original de Box-Pierce, la diferencia radica en que la autocorrelación muestral al cuadrado en el rezago \(k\) está ponderada por \((T + 2)∕(T − k)\). Para valores grandes de \(T\), estos pesos serán aproximadamente unitarios, por lo que los estadísticos \(Q_{LB}\) y \(Q_{BP}\) serán muy similares (bonus).

1.38. Elegir entre modelos que compiten

Introducción

• A menudo hay varios modelos que compiten, los cuales se pueden utilizar para predecir una serie temporal específica. Por ejemplo, existen varias formas de modelar y pronosticar tendencias. En consecuencia, seleccionar un modelo de pronóstico apropiado es de considerable importancia práctica.

• En esta sección discutimos algunos principios generales de selección de modelos. En capítulos posteriores, ilustraremos cómo se aplican estos principios en situaciones específicas.

• Al evaluar el ajuste del modelo a los datos históricos, hay varios criterios que pueden ser de valor. El error cuadrático medio de los residuos es

  \[ s^{2}=\frac{\displaystyle{\sum_{t=1}^{T}e_{t}^{2}}}{T-p} \]

  donde \(T\) periodos de datos se han utilizado para ajustar un modelo con \(p\) parámetros y \(e_{t}\) es el residuo del proceso de ajuste del modelo en el período \(t\). El error cuadrático medio \(s^{2}\) es simplemente la varianza muestral de los residuos y es un estimador de la varianza de los errores del modelo.

• Otro criterio es el estadístico \(R\)-cuadrado

  (1.6)\[ R^{2}=1-\frac{\displaystyle{\sum_{t=1}^{T}e_{t}^{2}}}{\displaystyle{\sum_{t=1}^{T}(y_{t}-\overline{y})^{2}}} \]

• El denominador de la Ecuación (1.6) es simplemente la suma total de cuadrados de las observaciones, que es constante (no depende del modelo), y el numerador es simplemente la suma residual de cuadrados.

Observación

• Seleccionar el modelo que maximiza el \(R^2\) es equivalente a seleccionar el modelo que minimiza la suma de los residuos al cuadrado. Valores grandes de \(R^2\) sugieren un buen ajuste a los datos históricos.

• Debido a que la suma residual de cuadrados siempre disminuye cuando se agregan parámetros a un modelo, confiar en \(R^2\) para seleccionar un modelo de pronóstico, fomenta el sobreajuste o la inclusión de más parámetros de los realmente necesarios para obtener buenos pronósticos. Un valor grande de \(R^2\) no garantiza que los errores de pronóstico fuera de la muestra a un paso adelante sean pequeños.

• Un mejor criterio es el estadístico \(R^2\) “ajustado”, definido como

  \[ R_{\text{Adj}}^{2}=1-\frac{\displaystyle{\sum_{t=1}^{T}e_{t}^{2}/(T-p)}}{\displaystyle{\sum_{t=1}^{T}(y_{t}-\overline{y})^{2}/(T-1)}}=\frac{s^{2}}{\displaystyle{\sum_{t=1}^{T}(y_{t}-\overline{y})^{2}/(T-1)}}. \]

• El ajuste es un ajuste “de tamaño”, es decir, ajusta según el número de parámetros en el modelo. Es importante destacar que un modelo que maximiza el estadístico \(R^2\) ajustado, también es el modelo que minimiza el cuadrado medio residual.

AIC y BIC

• Otros dos criterios importantes son el Criterio de Información de Akaike (AIC) [Akaike, 1974] y el Criterio de Información Bayesiano de Schwarz (abreviado como BIC o SIC por varios autores) [Schwarz, 1978]:

  \[ AIC=\ln\left(\frac{\displaystyle{\sum_{t=1}^{T}e_{t}^{2}}}{T}\right)+\frac{2p}{T}\quad\text{y}\quad BIC=\ln\left(\frac{\displaystyle{\sum_{t=1}^{T}e_{t}^{2}}}{T}\right)+\frac{p\ln(T)}{T}. \]

• Estos dos criterios penalizan la suma de los residuos al cuadrado por incluir parámetros adicionales en el modelo. Los modelos que tienen valores pequeños de AIC o BIC se consideran buenos modelos.

Observación

• Un criterio de selección de modelos es consistente si selecciona el modelo verdadero cuando el modelo verdadero está entre los considerados con una probabilidad que se aproxima a la unidad a medida que el tamaño de la muestra se vuelve grande.

• Resulta que \(s^{2}\), el \(R^2\) ajustado y el AIC no son consistentes, porque no penalizan lo suficiente por agregar parámetros. Confiar en estos criterios tiende a resultar en sobreajuste. El BIC, que tiene una penalización más fuerte por el “ajuste de tamaño”, es consistente.

• Los criterios de consistencia no revelan toda la situación. Aunque un criterio puede ser asintóticamente eficiente, como el AIC, esto no garantiza una selección ideal del modelo en situaciones donde el modelo verdadero y sus aproximaciones son altamente complejos.

AIC corregido

• Existen varias variaciones y extensiones de estos criterios. El AIC es un estimador sesgado de la discrepancia entre todos los modelos candidatos y el verdadero modelo. Esto ha llevado al desarrollo de una versión “corregida” del AIC [Hurvich and Tsai, 1989]:

  \[ AIC_{c}=\ln\left(\frac{\displaystyle{\sum_{t=1}^{T}e_{t}^{2}}}{T}\right)+\frac{2T(p+1)}{T-p-2}. \]

• Así, \(AIC_{c}\) es esencialmente AIC con un término adicional de penalización por el número de parámetros.

Observación

• A veces vemos que el primer término en el AIC, AICc o BIC se escribe como \(-2\ln L(\boldsymbol{\beta}, \sigma^{2})\), donde \(L(\boldsymbol{\beta}, \sigma^{2})\) es la función de verosimilitud para el modelo ajustado evaluado en las estimaciones de máxima verosimilitud de los parámetros desconocidos \(\boldsymbol{\beta}\) y \(\sigma^{2}\). En este contexto, AIC, AICc y SIC se llaman criterios de verosimilitud penalizados.

1.39. Análisis Exploratorio de Datos (EDA)

Observación

• Un Análisis Exploratorio de Datos (EDA) para series de tiempo debe abordar tanto los aspectos generales del conjunto de datos como las características específicas de las series temporales.

• Este enfoque sistemático garantiza que se identifiquen patrones relevantes, problemas y áreas de mejora antes de aplicar modelos predictivos o de pronóstico.

A continuación, se describe lo mínimo que debe incluir:

1. Introducción y contexto

• Objetivo del análisis: Explicar por qué se realiza el EDA (entender la estructura de los datos, identificar patrones, detectar anomalías, etc.).

• Descripción de los datos: Detallar la fuente, la frecuencia temporal (diaria, mensual, anual), la unidad de medida y la duración de la serie.

2. Análisis preliminar

   2.1. Inspección general

   • Dimensiones del conjunto de datos: Número de observaciones y variables.

   • Primeros y últimos valores: Revisión de los primeros y últimos registros para verificar coherencia temporal.

   • Valores faltantes: Identificar y cuantificar datos faltantes, y decidir cómo manejarlos (imputación, interpolación o eliminación).

   2.2. Estadísticas descriptivas

   • Promedio, mediana, desviación estándar, mínimo, máximo, percentiles.

   • Cálculo de métricas de dispersión (por ejemplo, rango intercuartílico).

3. Visualización de la serie

   3.1. Visualización temporal

   • Gráfica de línea: Para observar la tendencia general y posibles anomalías.

   • Gráficas desagregadas: Si hay múltiples series, visualizarlas por grupo o categoría.

   3.2. Análisis de componentes

   • Dividir la serie en componentes de tendencia, estacionalidad y residuales usando técnicas como:

   • Descomposición clásica (aditiva o multiplicativa).

   • Métodos como STL (Seasonal-Trend Decomposition using Loess).

   3.3. Detección de anomalías

   • Resaltar valores atípicos usando gráficos o algoritmos de detección de outliers.

4. Estacionalidad y periodicidad

   4.1. Análisis de patrones recurrentes

   • Gráficas de autocorrelación (ACF) y autocorrelación parcial (PACF):

   • Identificar patrones estacionales y dependencias temporales.

   • Diagramas de caja por periodo: Comparar distribuciones en ciclos recurrentes (meses, días, años).

   4.2. Transformación del dominio del tiempo

   • Agrupar por periodos relevantes (por ejemplo, promedio mensual, semanal).

   • Analizar patrones diarios, semanales, o anuales si la granularidad lo permite.

5. Análisis de tendencia

   • Identificar tendencias a largo plazo:

   • Usar suavizamiento exponencial o medias móviles.

   • Visualizar tendencias mediante líneas ajustadas (regresión lineal o polinómica).

6. Estabilidad de la serie

   6.1. Análisis de estacionariedad

   • Pruebas estadísticas: Aplicar pruebas como:

   • Dickey-Fuller aumentado (ADF).

   • KPSS (Kwiatkowski-Phillips-Schmidt-Shin).

   • Visualización de la media y varianza en submuestras: Evaluar si cambian con el tiempo.

   6.2. Transformaciones de datos

   • Aplicar logaritmos, diferencias o estandarización para estabilizar la varianza o hacer la serie estacionaria si es necesario.

7. Análisis multivariado (si aplica)

   • Correlación entre series: Identificar relaciones con otras series temporales mediante gráficos y matrices de correlación.

   • Gráficos de dispersión en el tiempo: Examinar relaciones no lineales o dependencias cruzadas.

8. Identificación de ciclos y frecuencia

   • Transformada de Fourier: Detectar frecuencias dominantes en la serie.

   • Espectro de potencia: Analizar la importancia relativa de diferentes ciclos.

9. Detección de anomalías y eventos extremos

   • Identificación visual: Marcar picos inusuales.

   • Modelos estadísticos: Aplicar pruebas para detectar outliers.

   • Eventos contextualizados: Relacionar anomalías con posibles eventos externos (económicos, climáticos, etc.).

10. Resumen y recomendaciones

    • Hallazgos clave: Resumir patrones importantes, estacionalidad, tendencias y anomalías.

    • Próximos pasos: Proponer acciones, como:

    • Ajustes para la modelización.

    • Métodos para manejar problemas detectados (no estacionariedad, valores atípicos, etc.).

Resumen

• Comenzamos este capítulo hablando de técnicas avanzadas de procesamiento de datos, como el remuestreo, el agrupamiento y el cálculo de ventanas móviles para obtener estadísticos agregados de una serie temporal. A continuación, describimos las series temporales estacionarias y analizamos las pruebas estadísticas de hipótesis como la prueba de Ljung-Box y la prueba de Dickey Fuller aumentada para verificar estacionariedad de una serie temporal.

• La estacionariedad de las series temporales no estacionarias es importante para la predicción de series temporales. Por lo tanto, discutimos dos enfoques diferentes para estacionar las series temporales. En primer lugar, el método de diferenciación, que abarca la primera, la segunda y la diferenciación estacional, se ha descrito para estacionar una serie temporal no estacionaria.

• En segundo lugar, la descomposición de las series temporales utilizando la librería statsmodels.tsa para modelos aditivos y multiplicativos. En el siguiente capítulo, se profundiza en las técnicas de suavización exponencial que tratan con datos de series temporales ruidosos.