2. Métodos de Suavización Exponencial

Introducción

• El presente capítulo trata del suavizado de datos en la señal de series temporales. El capítulo está organizado como sigue:

  • Introducción al suavizado de series temporales

  • Suavizado exponencial de primer orden

  • Suavizado exponencial de segundo orden

  • Suavizado exponencial de orden superior

2.1. Análisis

2.2. Introducción al suavizado de series temporales

• Los datos de las series temporales se componen de señal y ruido, donde la señal captura la dinámica intrínseca del proceso; sin embargo, el ruido representa el componente no modelado de la señal o error aleatorio no correlacionado, el cual en diferentes tiempos es estadísticamente independiente.

• La dinámica intrínseca de una señal de serie temporal puede ser tan simple como la media del proceso o puede ser una forma funcional compleja dentro de las observaciones, como se representa aquí:

  \[\begin{split} \\[1mm] y_{t}=f(t, \boldsymbol{\beta})+\varepsilon_{t},\quad\text{para}\quad i=1,2,3,\dots,T, \end{split}\]

  donde \(y_{t}\) representa las observaciones, \(\boldsymbol{\beta}\) es un vector de parámetros desconocidos, y \(\varepsilon_{t}\) es el error aleatorio no correlacionado, usualmente con media 0 y desviación 1.

• \(f(t, \boldsymbol{\beta})\) denota la forma funcional de la señal. Un ejemplo puede ser una constante (media) como forma funcional:

\[ y_{t}=\mu+\varepsilon_{t} \]

• Dado que \(\varepsilon_{t}\) es ruido blanco, este enfoque basado en el suavizado ayuda a separar la forma funcional intrínseca del ruido aleatorio, cancelándolo.

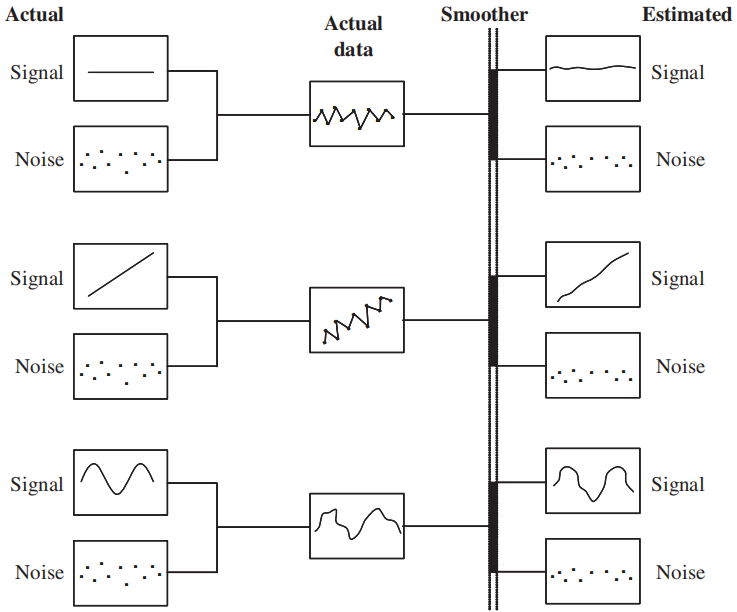
• Los métodos predictivos de suavización pueden considerarse como filtros que toman datos de entrada y separan los componentes de tendencia y de ruido, como se muestra en la Fig. 2.1

Fig. 2.1 Separación de componentes de tendencia y ruido.

• Un proceso constante puede ser suavizado reemplazando la observación actual con el mejor estimador para \(\mu\). Usando el criterio de mínimos cuadrados, definimos la suma de cuadrados de los errores \(SS_{E}\), para el proceso constante como

\[ SS_{E}=\sum_{t=1}^{T}(y_{t}-\mu)^{2}. \]

• La estimación por mínimos cuadrados de \(\mu\) puede ser calculada derivando \(SS_{E}\) con respecto a \(\mu\) el igualar a cero (verifíquelo). Esto entrega

  (2.1)\[ \hat{\mu}=\frac{1}{T}\sum_{t=1}^{T}y_{t}, \]

  donde \(\hat{\mu}\) es la estimación por mínimos cuadrados de \(\mu\).

• La Ecuación (2.1) muestra que la estimación por mínimos cuadrados de \(\mu\), es, en efecto, el promedio de las observaciones hasta el tiempo \(T\).

Observación

• El principal problema con el suavizador de la Ecuación (2.1) es que reacciona lentamente a procesos de cambios, debido a que acumula más y más puntos de datos ganando algún tipo de inercia. La solución más obvia es de alguna forma descontar datos más antiguos.

• Una solución común es usar la media móvil simple definida por

(2.2)\[ M_{T}= \frac{y_{T}+y_{T-1}+\cdots+y_{T-N+1}}{N}=\frac{1}{N}\sum_{t=T-N+1}^{N}y_{t}. \]

• Una media reaccionará más rápido a cambios si \(N\) es pequeño. Dado que para observaciones no correlacionadas con varianza constante \(\sigma^{2}\) se tiene que

  (2.3)\[ \text{Var}(M_{T})=\frac{\sigma^{2}}{N}. \]

• Dada la Ecuación (2.3). Si se espera que el proceso es constante, un valor grande de \(N\) puede ser usado, mientras que, un valor pequeño de \(N\) es preferido si el proceso es cambiante.

• Queda como ejercicio para el lector verificar que la función de autocorrelación (ACF) de la media móvil con \(k\)-lags está dada por (verifíquelo)

(2.4)\[\begin{split} \rho_{k}= \begin{cases} \displaystyle{1-\frac{|k|}{N}}, & k<N\\ 0, & k\geq N \end{cases}. \end{split}\]

2.3. Suavización exponencial de primer orden

Theorem 2.1 (Suavización exponencial simple)

• Dada una serie de tiempo \((y_{t})_{t=1}^{T}\). Una suavización exponencial ponderada está definida por:

  (2.5)\[ \sum_{t=0}^{T-1}\theta^{t}y_{T-t}=y_{T}+\theta y_{T-1}+\theta^{2}y_{t-2}+\cdots+\theta^{T-1}y_{1} \]

  donde \(\theta\) satisface \(|\theta|<1\). Esto es, observaciones pasadas son descontadas de manera geométricamente descendiente.

• La suavización exponencial simple \(\tilde{y}_{T}\) está representada por:

  \[ \tilde{y}_{T}=\lambda y_{T}+(1-\lambda)\tilde{y}_{T-1},\quad\text{donde}\quad\lambda=1-\theta. \]

  \(\lambda\) es conocido como el factor de descuento. Nótese que el factor de descuento \(\lambda\), representa el peso colocado sobre la última observación \(y_{T}\) y \(1-\lambda\) el peso asignado al valor suavizado de la previa observación \(\tilde{y}_{T-1}\).

Demostración

• Por hipótesis, pasadas observaciones son descontadas en forma geométricamente descendente, con \(|\theta|<1\). Nótese que el suavizador de la Ecuación (2.5) no es una media movil simple. En efecto:

\[\begin{split} \begin{align*} \sum_{t=0}^{T-1}\theta^{t}&=1+\theta+\theta^2+\cdots+\theta^{T-1},\quad\text{multiplicando por}~(1-\theta)\\ (1-\theta)\sum_{t=0}^{T-1}\theta^{t}&=(1-\theta)(1+\theta+\theta^2+\cdots+\theta^{T-1})\\ &=(1+\theta+\theta^2+\cdots+\theta^{T-1})-(\theta+\theta^2+\theta^{3}+\cdots+\theta^{T-1}+\theta^{T})\\[3mm] &=1-\theta^{T}\Longrightarrow\\ \sum_{t=0}^{T-1}\theta^{t}&=\frac{1-\theta^{T}}{1-\theta}. \end{align*} \end{split}\]

• Nótese que la sumatoria:

  \[ \sum_{t=0}^{T-1}\theta^{t}=\frac{1-\theta^{T}}{1-\theta}, \]

  no necesariamente es igual a 1 (propiedad de los promedios). Esto puede ser ajustado multiplicando la Ecuación (2.5) por \((1-\theta)/(1-\theta^{T})\).

• Además, dado que \((1-\theta)/(1-\theta^{T})\rightarrow 1-\theta\) para valores grandes de \(T\), \(~|\theta|<1\). Entonces, la Ecuación (2.5) puede reescribirse como:

\[\begin{split} \begin{align*} \tilde{y}_{T}&=\frac{1-\theta}{1-\theta^{T}}\sum_{t=0}^{T-1}\theta^{t}y_{T-t}\\ &=(1-\theta)\sum_{t=0}^{T-1}\theta^{t}y_{T-t},~\text{para valores grandes de $T$}\\ &=(1-\theta)(y_{T}+\theta y_{T-1}+\theta^{2}y_{T-2}+\cdots+\theta^{T-1}y_{1}) \end{align*} \end{split}\]

• Entonces la suavización exponencial simple está dada por

(2.6)\[ \tilde{y}_{T}=(1-\theta)(y_{T}+\theta y_{T-1}+\theta^{2}y_{T-2}+\cdots+\theta^{T-1}y_{1}) \]

• Una expresión alternativa para la suavización exponencial simple es:

\[\begin{split} \begin{align*} \tilde{y}_{T}&=(1-\theta)(y_{T}+\theta y_{T-1}+\theta^{2}y_{T-2}+\cdots+\theta^{T-1}y_{1}\\ &=(1-\theta)y_{T}+(1-\theta)(\theta y_{T-1}+\theta^{2}y_{T-2}+\cdots+\theta^{T-1}y_{1})\\ &=(1-\theta)y_{T}+\theta(1-\theta)(y_{T-1}+\theta y_{T-2}+\cdots+\theta^{T-2}y_{1})\\ &=(1-\theta)y_{T}+\theta\tilde{y}_{T-1}. \end{align*} \end{split}\]

• Esto es, la suavización exponencial de primer orden, puede verse como combinación lineal de la observación actual y la observación suavizada en un tiempo previo. Definiendo \(\lambda=1-\theta\), (factor de corrección) se tiene que:

(2.7)\[ \tilde{y}_{T}=\lambda y_{T}+(1-\lambda)\tilde{y}_{T-1}. \]

Observación

Análogamente a la longitud del periodo en la media movil, un asunto importante para la suavización exponencial es la selección del factor de descuento \(\lambda\). Además, a partir de la Ecuación (2.7) podemos observa que el cálculo de \(\tilde{y}_{1}\) va a requerir conocer \(\tilde{y}_{0}\).

Theorem 2.2 (Selección de \(\tilde{y}_{0}\))

Dada una serie de tiempo \((y_{t})_{t=1}^{T}\), donde \(T\) es grande, la contribución de \(\tilde{y}_{0}\) a \(\tilde{y}_{T}\) es mínima. Por lo tanto, la estimación de \(\tilde{y}_{0}\) tiene poca influencia sobre la suavización. Sin embargo, dos estimaciones de \(\tilde{y}_{0}\) comunmente usadas en las aplicaciones son las siguientes:

1. \(\tilde{y}_{0}=y_{1}\): Si los cambios esperados del proceso ocurren temprano y rápido, esta selección para el valor inicial de \(\tilde{y}_{T}\) es razonable.

2. \(\tilde{y}_{0}=\overline{y}\): Tomar el promedio de los datos disponibles. Si el proceso es constante, al menos al inicio, este sería el valor mas adecuado.

Demostración

• Dado que \(\tilde{y}_{0}\) es necesario en el calculo recursivo que inicia con: \(\tilde{y}_{1}=\lambda y_{1}+(1-\lambda)\tilde{y}_{0}\), estimamos su valor a partir de la Ecuación (2.7)

\[\begin{split} \begin{align*} \tilde{y}_{1}&=\lambda y_{1}+(1-\lambda)\tilde{y}_{0}\\ \tilde{y}_{2}&=\lambda y_{2}+(1-\lambda)\tilde{y}_{1}=\lambda y_{2}+(1-\lambda)(\lambda y_{1}+(1-\lambda)\tilde{y}_{0})=\lambda(y_{2}+(1-\lambda)y_{1})+(1-\lambda)^{2}\tilde{y}_{0}\\ \tilde{y}_{3}&=\lambda y_{3}+(1-\lambda)\tilde{y}_{2}=\lambda y_{3}+(1-\lambda)(\lambda(y_{2}+(1-\lambda)\tilde{y}_{1})+(1-\lambda)^{2}\tilde{y}_{0})\\ &=\lambda(y_{3}+(1-\lambda)y_{2}+(1-\lambda)^{2}y_{1})+(1-\lambda)^{3}\tilde{y}_{0}\\ &\vdots\\ \tilde{y}_{T}&=\lambda(y_{T}+(1-\lambda)y_{T-1}+(1-\lambda)^{2}y_{T-2}+\cdots+(1-\lambda)^{T-1}y_{1})+(1-\lambda)^{T}\tilde{y}_{0} \end{align*} \end{split}\]

• Por lo tanto, cuando \(T\) se hace grande, \(~(1-\lambda)^{T}\) se hace pequeño, esto es, la contribución de \(\tilde{y}_{0}\) a \(\tilde{y}_{T}\) es mínima. Esto es, la estimación de \(\tilde{y}_{0}\) no es relevante para un conjunto grande de datos.

2.4. El valor de \(\lambda\)

Observación

• En general, cuando \(\lambda\) tiende a 1, y se hace más hincapié en la última observación, los valores suavizados se aproximarán a las observaciones originales.

• Si \(\lambda=0\), los valores suavizados serán todos igual a una constante, a saber \(\tilde{y}_{0}\). Esta línea constante sería la versión más suavizada de cualquier patrón que siga la serie de tiempo original.

• Para \(\lambda=1\), tenemos \(\tilde{y}_{T}=y_{T}\) y este representará la versión menos suavizada de la serie de tiempo original.

• Con base en la selección de \(\lambda\), esperamos acordemente que la varianza varíe entre 0 y la varianza de la serie de tiempo original.

• Nótese que bajo el supuesto de independencia y varianza constante tenemos que

\[\begin{split} \begin{align} \text{Var}(\tilde{y}_{T}) &= \text{Var}\left(\lambda\sum_{t=0}^{\infty}(1-\lambda)^{t}y_{T-t}\right)\\ &= \lambda^{2}\sum_{t=0}^{\infty}(1-\lambda)^{2t}\text{Var}(y_{T-t})\\ &= \lambda^{2}\sum_{t=0}^{\infty}(1-\lambda)^{2t}\text{Var}(y_{T})\\ &= \text{Var}(y_{T})\lambda^{2}\sum_{t=0}^{\infty}(1-\lambda)^{2t} \end{align} \end{split}\]

• Observe que

\[ \sum_{t=0}^{T-1}(1-\lambda)^{2t}=1+(1-\lambda)^{2}+(1-\lambda)^{4}+\cdots+(1-\lambda)^{2(T-1)} \]

• Multiplicando por \(1-(1-\lambda)^{2}\) se tiene que:

\[\begin{split} \begin{align*} (1-(1-\lambda)^{2})\sum_{t=0}^{T-1}(1-\lambda)^{2t} &= 1+(1-\lambda)^{2}+(1-\lambda)^{4}+\cdots+(1-\lambda)^{2(T-1)}\\ &- ((1-\lambda)^{2}+(1-\lambda)^{4}+\cdots+(1-\lambda)^{2T})\\[3mm] &= 1-(1-\lambda)^{2T}\rightarrow 1,\quad\text{para valores grandes de}~T, |1-\lambda|<1\Rightarrow\\ \sum_{t=0}^{T-1}(1-\lambda)^{2t} &= \frac{1}{\lambda(2-\lambda)} \end{align*} \end{split}\]

• Por lo tanto,

\[ \begin{align} \text{Var}(\tilde{y}_{T}) = \text{Var}(y_{T})\lambda^{2}\sum_{t=0}^{\infty}(1-\lambda)^{2t} = \text{Var}(y_{T})\lambda^{2}\frac{1}{\lambda(2-\lambda)} = \frac{\lambda}{2-\lambda}\text{Var}(y_{T}) \end{align} \]

• Nótese que si \(\lambda\rightarrow1\), \(\text{Var}(\tilde{y}_{T})\rightarrow\text{Var}(y_{T})\), y si \(\lambda\rightarrow0\), \(\text{Var}(\tilde{y}_{T})\rightarrow0\). La pregunta ahora es, ¿cuánto suavizado se necesita?. En la literatura se recomienda \(\lambda\) entre 0.1 y 0.4 y, de hecho, funcionan bien en la práctica. Un método más riguroso para encontrar el valor \(\lambda\) se discutirá más adelante en este capítulo.

• Como medidas de precisión usaremos las siguientes métricas las cuales vienen ya implementadas en Python; MAPE, MAD y MSD.

• El error porcentual medio absoluto (MAPE) es el cambio porcentual medio absoluto entre el valor predicho, esto es \(\tilde{y}_{t-1}:=\tilde{y}_{t}(t-1)\), para una predicción one-step-ahead y el valor real dado por

\[ \text{MAPE}=\frac{\displaystyle{\sum_{t=1}^{T}|(y_{t}-\tilde{y}_{t-1})/y_{t}|}}{T}\times 100,\quad (y_{t}\neq 0). \]

• La desviación media absoluta (MAD) es la diferencia absoluta media entre los valores predichos y los verdaderos, dada por

\[ \text{MAD}=\frac{\displaystyle{\sum_{t=1}^{T}|(y_{t}-\tilde{y}_{t-1})|}}{T}. \]

• La desviación cuadrática media (MSD) es la diferencia cuadrática media entre los valores predichos y los verdaderos, dada por

\[ \text{MSD}=\frac{\displaystyle{\sum_{t=1}^{T}(y_{t}-\tilde{y}_{t-1})^{2}}}{T}. \]

2.5. Implementación \(SES\)

import pandas as pd
from matplotlib import pyplot as plt
import seaborn as sns
import warnings
warnings.filterwarnings("ignore")
sns.set_style("darkgrid")

djia_df = pd.read_excel('/home/lihkir/Data/DJIA_Jan2016_Dec2016.xlsx')

djia_df['Date'] = pd.to_datetime(djia_df['Date'], '%Y-%m-%d')
djia_df.index = djia_df['Date']
djia_df.drop('Date', axis=1, inplace=True)
djia_df.head()

	Open	High	Low	Close	Adj Close	Volume
Date
2016-01-04	17405.480469	17405.480469	16957.630859	17148.939453	17148.939453	148060000
2016-01-05	17147.500000	17195.839844	17038.609375	17158.660156	17158.660156	105750000
2016-01-06	17154.830078	17154.830078	16817.619141	16906.509766	16906.509766	120250000
2016-01-07	16888.359375	16888.359375	16463.630859	16514.099609	16514.099609	176240000
2016-01-08	16519.169922	16651.890625	16314.570313	16346.450195	16346.450195	141850000

djia_ts = pd.Series(data=djia_df['Close'].values, index=djia_df.index)

djia_ts.head()

Date
2016-01-04    17148.939453
2016-01-05    17158.660156
2016-01-06    16906.509766
2016-01-07    16514.099609
2016-01-08    16346.450195
dtype: float64

plt.rcParams['text.usetex'] = True

plt.figure()
djia_ts.plot(color='b')
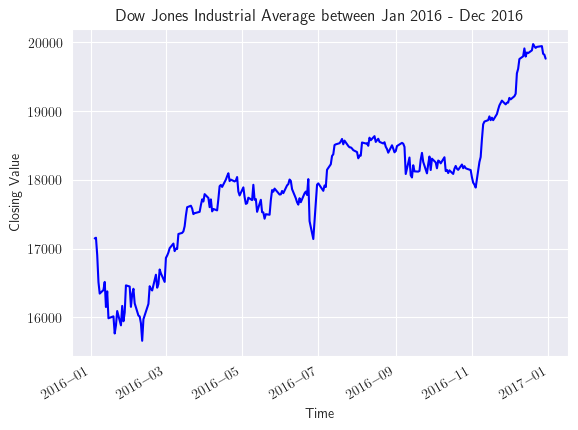
plt.title('Dow Jones Industrial Average between Jan 2016 - Dec 2016')
plt.xlabel('Time')
plt.ylabel('Closing Value');

def firstsmooth(y, lambda_, start=None):
    ytilde = y.copy()
    if start is None:
        start = y[0]
    ytilde[0] = lambda_ * y[0] + (1 - lambda_) * start
    for i in range(1, len(y)):
        ytilde[i] = lambda_ * y[i] + (1 - lambda_) * ytilde[i - 1]
    return ytilde

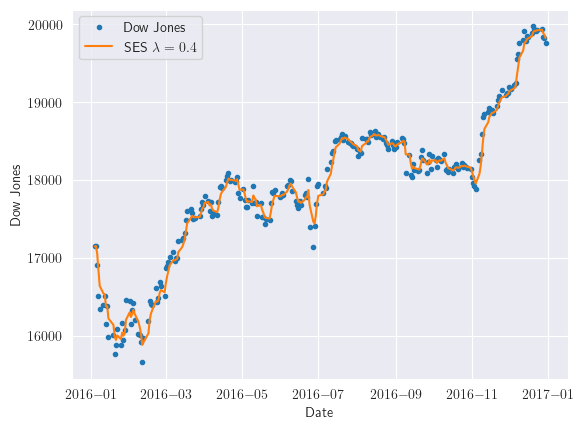
dji_smooth1 = firstsmooth(y=djia_ts, lambda_=0.4)

plt.plot(djia_ts, marker='o', linestyle='', markersize=3, label='Dow Jones')
plt.plot(dji_smooth1, label='SES $\lambda=0.4$')
plt.xlabel('Date')
plt.ylabel('Dow Jones')
plt.legend()
plt.show()

def measacc_fs(y, lambda_):
    out = firstsmooth(y, lambda_)
    T = len(y)
    yh = y.copy().values
    out = pd.concat([pd.Series([y[0]]), out.iloc[:-1]], ignore_index=True).values
    prederr = yh - out
    SSE = sum(prederr**2)
    MAPE = 100 * sum(abs(prederr / yh)) / T
    MAD = sum(abs(prederr)) / T
    MSD = sum(prederr**2) / T
    ret1 = pd.DataFrame({
        "SSE": [SSE],
        "MAPE": [MAPE],
        "MAD": [MAD],
        "MSD": [MSD]
    })
    ret1.reset_index(drop=True, inplace=True)
    return ret1

measacc_fs(djia_ts, 0.4)

	SSE	MAPE	MAD	MSD
0	6.844383e+06	0.689939	121.602389	27160.251204

from statsmodels.tsa.holtwinters import ExponentialSmoothing

def measacc_hw(y, lambda_):
    model = ExponentialSmoothing(y.values)
    fit = model.fit(smoothing_level=lambda_)
    T = len(y)
    yh = y.copy().values
    y_pred = pd.Series(data=fit.fittedvalues, index=y.index)
    out = pd.concat([pd.Series([y[0]]), y_pred[:-1]], ignore_index=True).values
    prederr = yh - out
    SSE = sum(prederr**2)
    MAPE = 100 * sum(abs(prederr / yh)) / T
    MAD = sum(abs(prederr)) / T
    MSD = sum(prederr**2) / T
    ret1 = pd.DataFrame({
        "SSE": [SSE],
        "MAPE": [MAPE],
        "MAD": [MAD],
        "MSD": [MSD]
    })
    ret1.reset_index(drop=True, inplace=True)
    return ret1

measacc_hw(djia_ts, 0.4)

	SSE	MAPE	MAD	MSD
0	1.084431e+07	0.876061	154.763888	43032.984921

• En este caso, se obtuvo un MAPE del 0.87% lo cual significa que, en promedio, las predicciones tienen un error del 0.87% en relación con los valores reales, el cual es más alto que el implementado en la función firstsmooth.

2.6. Modelado de datos de series temporales

Theorem 2.3

• Considere un proceso constante, esto es, un proceso donde los datos de series de tiempo se espera que varíen en torno a un nivel constante, con fluctuaciones aleatorias, las cuales son caracterizadas usualmente por errores no correlacionados con media 0 y varianza constante.

• La clase general de modelos puede expresarse como

  \[ y_{t}=f(t, \boldsymbol{\beta})+\varepsilon_{t}, \]

  donde \(\boldsymbol{\beta}\) es un vector de parámetros desconocidos y \(\varepsilon_{t}\) representa errores no correlacionados.

• El proceso constante es miembro de esta clase general:

  \[ y_{t}=\beta_{0}+\varepsilon_{t}, \]

  donde \(\beta_{0}\) es igual a \(\mu\).

• Entonces, la estimación de mínimos cuadrados ponderada de \(\beta_{0}\) en el proceso constante, con pesos exponencialmente decrecientes en el tiempo es

\[ \hat{\beta}_{0}=(1-\theta)\sum_{t=0}^{T-1}\theta^{t}y_{T-t}. \]

Demostración

• Consideremos la suma de errores cuadráticos para el proceso constante, dada por

\[ SS_{E}=\sum_{t=1}^{T}(y_{t}-\mu)^{2} \]

• Si afirmamos que no todas las observaciones deberían tener igual influencia sobre la suma, introducimos una cadena de pesos geométricamente decrecientes en tiempo

(2.8)\[ SS_{E}^{\star}=\sum_{t=0}^{T-1}\theta^{t}(y_{T-t}-\beta_{0})^{2},~\text{donde}~|\theta|<1. \]

• Derivando la Ecuación (2.8) con respecto a \(\beta_{0}\) e igualando a cero obtenemos el estimador por mínimos cuadrados para \(\beta_{0}\)

\[ \begin{align*} \frac{\partial SS_{E}^{\star}}{\partial\beta_{0}} &= \frac{\partial}{\partial\beta_{0}}\left(\sum_{t=0}^{T-1}\theta^{t}(y_{T-t}-\beta_{0})^{2}\right)=-2\sum_{t=0}^{T-1}\theta^{t}(y_{T-t}-\beta_{0})=0 \end{align*} \]

• Dado que \(\sum_{t=0}^{T-1}\theta^{t}=(1-\theta^{T})/(1-\theta)\), entonces

\[ \hat{\beta}_{0}=\frac{1-\theta}{1-\theta^{T}}\sum_{t=0}^{T-1}\theta^{t}y_{T-t}\rightarrow(1-\theta)\sum_{t=0}^{T-1}\theta^{t}y_{T-t},\quad\text{para valores grandes de}~T. \]

• Nótese que \(\hat{\beta}_{0}=\tilde{y}_{T}\). Esto es, el proceso de suavización exponencial simple en efecto provee una estimación de mínimos cuadrados ponderada de \(\beta_{0}\), para el proceso constante con pesos que son exponencialmente decrecientes en el tiempo.

Observación

• Retomando con nuestra clase de modelo general \(y_{t}=f(t; \boldsymbol{\beta})+\varepsilon_{t},~f(t, \boldsymbol{\beta})\) puede ser cualquier función de \(t\).

• Por ejemplo, para series de tiempo no estacionarias, es mas conveniente considerar una familia polinómica, donde el proceso constante es el modelos mas simple que podemos considerar.

2.7. Suavización exponencial de segundo orden

Theorem 2.4

• Un modelo apropiado en tiempo para tendencias lineales está dado por:

  \[ y_{t}=\beta_{0}+\beta_{1}t+\varepsilon_{t}, \]

  donde \(\varepsilon_{t}\) es no correlacionado con media 0 y varianza constante \(\sigma_{\varepsilon}^{2}\).

• Demuestre que el suavizador exponencial simple es un estimador sesgado para el modelo de tendencia lineal y la cantidad de sesgo es: \(-(1-\lambda)\beta_{1}/\lambda\), donde

\[ \text{E}(\tilde{y}_{T})=\beta_{0}+\beta_{1}T-\frac{1-\lambda}{\lambda}\beta_{1}=\text{E}(y_{T})-\frac{1-\lambda}{\lambda}\beta_{1}. \]

• Dada la suavización exponencial de segundo orden definida por:

  \[ \tilde{y}_{T}^{(2)}=\lambda\tilde{y}_{T}^{(1)}+(1-\lambda)\tilde{y}_{T-1}^{(2)}, \]

  donde \(\tilde{y}_{T}^{(1)}, \tilde{y}_{T}^{(2)}\) denotan las suavizaciones exponenciales de primer y segundo orden respectivamente, demuestre que el predictor de \(\tilde{y}_{T}\) está dado por

  \[ \tilde{y}_{T}=2\tilde{y}_{T}^{(1)}-\tilde{y}_{T}^{(2)}. \]

• Puede demostrarse además que \(\tilde{y}_{T}\) es insesgado.

Demostración

• Bajo el supuesto de independencia sobre \((y_{t})_{t=1}^{\infty}\), calculamos suavización exponencial para datos de series de tiempo que exhiben tendencia lineal

\[ \text{E}(\tilde{y}_{T})=\text{E}\left(\lambda\sum_{t=0}^{T-1}(1-\lambda)^{t}y_{T-t}\right)=\lambda\sum_{t=0}^{T-1}(1-\lambda)^{t}\text{E}(y_{T-t}). \]

• Dado que para la tendencia lineal: \(\text{E}(y_{t})=\text{E}(\beta_{0}+\beta_{1}t+\varepsilon_{t})=\beta_{0}+\beta_{1}t\), entonces

\[\begin{split} \begin{align*} \text{E}(\tilde{y}_{T}) &= \lambda\sum_{t=0}^{T-1}(1-\lambda)^{t}(\beta_{0}+\beta_{1}(T-t))\\ &= \lambda\sum_{t=0}^{T-1}(1-\lambda)^{t}(\beta_{0}+\beta_{1}T)-\lambda\sum_{t=0}^{T-1}(1-\lambda)^{t}(\beta_{1}t)\\ &= (\beta_{0}+\beta_{1}T)\lambda\sum_{t=0}^{T-1}(1-\lambda)^{t}-\lambda\beta_{1}\sum_{t=0}^{T-1}(1-\lambda)^{t}t. \end{align*} \end{split}\]

• Dado que \(|1-\lambda|<1\) se tiene que \(\sum_{t=0}^{T-1}(1-\lambda)^{t}=1/(1-(1-\lambda))=1/\lambda\). Nótese además que

\[\begin{split} \begin{align*} \sum_{t=0}^{\infty}(1-\lambda)^{t}t&=(1-\lambda)\sum_{t=0}^{\infty}t(1-\lambda)^{t-1}\\ &= -(1-\lambda)\sum_{t=0}^{\infty}\frac{\partial}{\partial\lambda}(1-\lambda)^{t}\\ &= -(1-\lambda)\frac{\partial}{\partial\lambda}\left(\sum_{t=0}^{\infty}(1-\lambda)^{t}\right)\\ &= -(1-\lambda)\frac{\partial}{\partial\lambda}\left(\frac{1}{1-(1-\lambda)}\right)\\ &= -(1-\lambda)\frac{\partial}{\partial\lambda}\left(\frac{1}{\lambda}\right)=-(1-\lambda)\left(-\frac{1}{\lambda^{2}}\right)=\frac{1-\lambda}{\lambda^{2}}. \end{align*} \end{split}\]

• Reemplazando en \(\text{E}(\tilde{y}_{T})\) se tiene que

\[ \text{E}(\tilde{y}_{T})=(\beta_{0}+\beta_{1}T)\lambda\left(\frac{1}{\lambda}\right)-\lambda\beta_{1}\left(\frac{1-\lambda}{\lambda^{2}}\right)=(\beta_{0}+\beta_{1}T)-\frac{1-\lambda}{\lambda}\beta_{1}=\text{E}(y_{T})-\frac{1-\lambda}{\lambda}\beta_{1}. \]

• Esto es

(2.9)\[ \text{E}(\tilde{y}_{T})=\text{E}(y_{T})-\frac{1-\lambda}{\lambda}\beta_{1}. \]

• Esto es, la suavización exponencial simple es sesgada como estimador y la cantidad de sesgo está dada por \(-(1-\lambda)\beta_{1}/\lambda\), la cual puede generar errores de subestimación.

• Una solución puede ser usar \(\lambda\) grande, ya que \((1-\lambda)/\lambda\rightarrow0\) cuando \(\lambda\rightarrow1\). Técnicas autoadaptativas para \(\lambda\) pueden ser estudiadas, las cuales sigan los cambios en el proceso.

• Dado que la suavización de segundo orden está dada por

  \[ \tilde{y}_{T}^{(2)}=\lambda\tilde{y}_{T}^{(1)}+(1-\lambda)y_{T-1}^{(2)}, \]

  esto es, \(\tilde{y}_{T}^{(2)}\) es obtenida aplicando suavización exponencial simple a \(\tilde{y}_{T}\).

• Por motivos de derivación de la expresión, consideramos el mismo \(\lambda\) para \(\tilde{y}_{T}^{(1)}\) y \(\tilde{y}_{t}^{(2)}\). Dado que la suavización exponencial de primer orden es sesgada, su suavización (suavización de segundo orden) también es sesgada. Entonces

\[ \text{E}(\tilde{y}_{T}^{(2)})=\text{E}(\tilde{y}_{T}^{(1)})-\frac{1-\lambda}{\lambda}\beta_{1}. \]

• Además

\[ \frac{1-\lambda}{\lambda}\beta_{1}=\text{E}(\tilde{y}_{T}^{(1)})-\text{E}(\tilde{y}_{T}^{(2)})\Rightarrow\tilde{y}_{T}^{(1)}-\tilde{y}_{T}^{(2)}=\frac{1-\lambda}{\lambda}\beta_{1},~\text{entonces} \]

(2.10)\[ \textcolor{red}{\hat{\beta}_{1, T}=\frac{\lambda}{1-\lambda}(\tilde{y}_{T}^{(1)}-\tilde{y}_{T}^{(2)})}. \]

• Usando la Ecuación (2.9) tenemos que: \(\text{E}(\tilde{y}_{T}^{(1)})=(\hat{\beta}_{0, T}+\hat{\beta}_{1, T}T)-(1-\lambda)\hat{\beta}_{1, T}/\lambda\), entonces, análogamente

(2.11)\[ \textcolor{red}{\hat{\beta}_{0, T}=\tilde{y}_{T}^{(1)}-T\hat{\beta}_{1, T}+\displaystyle{\frac{1-\lambda}{\lambda}}\hat{\beta}_{1, T}.} \]

• Reescribiendo \(\hat{\beta}_{0, T}\) en términos de \(\tilde{y}_{T}^{(1)}\) y \(\tilde{y}_{T}^{(2)}\) obtenemos

\[\begin{split} \begin{align*} \hat{\beta}_{0, T} &= \tilde{y}_{T}^{(1)}-T\left(\frac{\lambda}{1-\lambda}(\tilde{y}_{T}^{(1)}-\tilde{y}_{T}^{(2)})\right)+\frac{1-\lambda}{\lambda}\left(\frac{\lambda}{1-\lambda}(\tilde{y}_{T}^{(1)}-\tilde{y}_{T}^{(2)})\right)\\ &= \tilde{y}_{T}^{(1)}-T\frac{\lambda}{1-\lambda}(\tilde{y}_{T}^{(1)}-\tilde{y}_{T}^{(2)})+(\tilde{y}_{T}^{(1)}-\tilde{y}_{T}^{(2)})\\ &= \left(2-T\frac{\lambda}{1-\lambda}\right)\tilde{y}_{T}^{(1)}-\left(1-T\frac{\lambda}{1-\lambda}\right)y_{T}^{(2)}, \end{align*} \end{split}\]

• Entonces

(2.12)\[ \textcolor{red}{\hat{\beta}_{0, T} = \left(2-T\frac{\lambda}{1-\lambda}\right)\tilde{y}_{T}^{(1)}-\left(1-T\frac{\lambda}{1-\lambda}\right)y_{T}^{(2)}}, \]

• Combinando las Ecuaciones (2.10)-(2.12) tenemos que

\[\begin{split} \begin{align*} \tilde{y}_{T} &= \hat{\beta}_{0, T}+\hat{\beta}_{1, T}T=\left(2-T\frac{\lambda}{1-\lambda}\right)\tilde{y}_{T}^{(1)}-\left(1-T\frac{\lambda}{1-\lambda}\right)\tilde{y}_{T}^{(2)}+\frac{\lambda}{1-\lambda}(\tilde{y}_{T}^{(1)}-\tilde{y}_{T}^{(2)})T\\ &= \left(2-T\frac{\lambda}{1-\lambda}+T\frac{\lambda}{1-\lambda}\right)\tilde{y}_{T}^{(1)}-\left(1-T\frac{\lambda}{1-\lambda}+T\frac{\lambda}{1-\lambda}\right)\tilde{y}_{T}^{(2)}\\[2mm] &=2\tilde{y}_{T}^{(1)}-\tilde{y}_{T}^{(2)}. \end{align*} \end{split}\]

• Entonces

(2.13)\[ \textcolor{red}{\tilde{y}_{T}=2\tilde{y}_{T}^{(1)}-\tilde{y}_{T}^{(2)}} \]

• Nótese que como

\[ \text{E}(\tilde{y}_{T}^{(1)}) = (\beta_{0}+\beta_{1}T)-\frac{1-\lambda}{\lambda}\beta_{1}\Rightarrow\tilde{y}_{T}^{(1)}=(\hat{\beta}_{0, T}+\hat{\beta}_{1, T}T)-\frac{1-\lambda}{\lambda}\hat{\beta}_{1, T} \]

• Y además

\[\begin{split} \begin{align*} \text{E}(\tilde{y}_{T}^{(2)}) &= \text{E}(\tilde{y}_{T}^{(1)})-\frac{1-\lambda}{\lambda}\hat{\beta}_{1, T}=\text{E}\left((\hat{\beta}_{0, T}+\hat{\beta}_{1, T}T)-\frac{1-\lambda}{\lambda}\hat{\beta}_{1, T}\right)-\frac{1-\lambda}{\lambda}\hat{\beta}_{1, T}\\ &= (\hat{\beta}_{0, T}+\hat{\beta}_{1, T})-\frac{1-\lambda}{\lambda}\hat{\beta}_{1, T}-\frac{1-\lambda}{\lambda}\hat{\beta}_{1, T}=(\hat{\beta}_{0, T}+\hat{\beta}_{1, T})-2\left(\frac{1-\lambda}{\lambda}\right)\hat{\beta}_{1, T}\\ &\Rightarrow\tilde{y}_{T}^{(2)}=(\hat{\beta}_{0, T}+\hat{\beta}_{1, T})-2\left(\frac{1-\lambda}{\lambda}\right)\hat{\beta}_{1, T} \end{align*} \end{split}\]

• Entonces

\[\begin{split} \textcolor{red}{ \begin{align*} \tilde{y}_{T}^{(1)} &= (\hat{\beta}_{0, T}+\hat{\beta}_{1, T})-\frac{1-\lambda}{\lambda}\hat{\beta}_{1, T}\\ \tilde{y}_{T}^{(2)} &= (\hat{\beta}_{0, T}+\hat{\beta}_{1, T})-2\left(\frac{1-\lambda}{\lambda}\right)\hat{\beta}_{1, T} \end{align*} } \end{split}\]

• Con los respectivos valores iniciales

\[\begin{split} \begin{align*} \tilde{y}_{0}^{(1)} &= \hat{\beta}_{0, 0}-\frac{1-\lambda}{\lambda}\hat{\beta}_{1, 0}\\ \tilde{y}_{0}^{(2)} &= \hat{\beta}_{0, 0}-2\left(\frac{1-\lambda}{\lambda}\right)\hat{\beta}_{1, 0} \end{align*} \end{split}\]

• La estimación de los parámetros iniciales es obtenida usualmente por medio del método de mínimos cuadrado. Por ejemplo, los parámetros \(\hat{\beta}_{0, 0}, \hat{\beta}_{1, 0}\) asociados al US Consumer Prices Index (CPI) de Enero 1995 a Diciembre 2004, obtenidos por mínimos cuadrados están dados por \(\hat{\beta}_{0, 0}=149.89\) y \(\hat{\beta}_{1, 0}=0.3\). Usando \(\lambda=0.3\) se tiene que

\[\begin{split} \begin{align} \hat{y}_{0}^{(1)} &= \hat{\beta}_{0, 0}-\frac{1-\lambda}{\lambda}\hat{\beta}_{1, 0}=149.89-\frac{1-0.3}{0.3}0.3=146.22\\ \hat{y}_{0}^{(2)} &= \hat{\beta}_{0, 0}-2\frac{1-\lambda}{\lambda}\hat{\beta}_{1, 0}=149.89-2\frac{1-0.3}{0.3}0.3=142.56\\ \end{align} \end{split}\]

2.8. Implementación \(DES\)

import matplotlib.pyplot as plt

cpi_smooth1 = firstsmooth(y=djia_ts, lambda_=0.3)
cpi_smooth2 = firstsmooth(y=cpi_smooth1, lambda_=0.3)

cpi_hat = 2 * cpi_smooth1 - cpi_smooth2

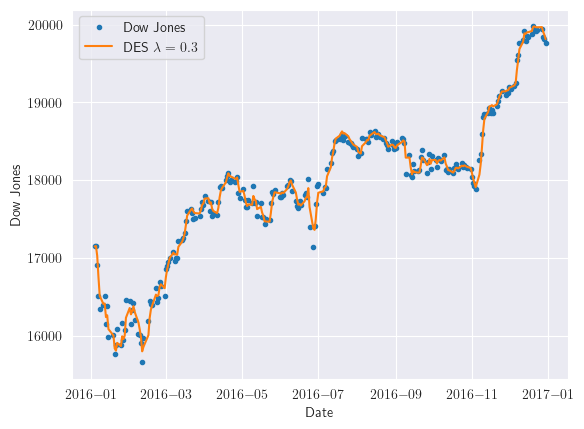
plt.plot(djia_ts, marker='o', linestyle='', markersize=3, label='Dow Jones')
plt.plot(cpi_hat, label='DES $\lambda=0.3$')
plt.xlabel('Date')
plt.ylabel('Dow Jones')
plt.legend()
plt.show()

2.9. Suavización exponencial de alto orden

• Hasta ahora hemos discutido el uso de suavizadores exponenciales al estimar los modelos de tendencia constante y lineal. Para el primero empleamos el suavizador exponencial simple o de primer orden y para el segundo el suavizador exponencial de segundo orden. Además, se puede demostrar que para el modelo polinómico general de \(n\text{th}\)-ésimo grado de la forma

  (2.14)\[ y_{t}=\beta_{0}+\beta_{1}t+\frac{\beta_{2}}{2!}t^{2}+\cdots+\frac{\beta_{n}}{n!}t^{n}+\varepsilon_{t}, \]

  donde \(\varepsilon_{t}\) se supone independiente con media 0 y varianza constante \(\sigma_{\varepsilon}^{2}\), empleamos suavizadores exponenciales de orden \(n-1\)

  \[\begin{split} \begin{align*} \tilde{y}_{T}^{(1)} &= \lambda y_{T}+(1-\lambda)\tilde{y}_{T-1}^{(1)}\\ \tilde{y}_{T}^{(2)} &= \lambda \tilde{y}_{T}^{(1)}+(1-\lambda)\tilde{y}_{T-1}^{(2)}\\ &\vdots\\ \tilde{y}_{T}^{(n)} &= \lambda \tilde{y}_{T}^{(n-1)}+(1-\lambda)\tilde{y}_{T-1}^{(n)}, \end{align*} \end{split}\]

  para estimar los parámetros del modelo.

Observación

• Incluso para el modelo cuadrático, los cálculos se vuelven bastante complicados. Consulte [Montgomery et al., 1990], [Brown, 2004] y [Abraham and Ledolter, 2009] para las soluciones a problemas de suavizamiento exponencial de orden superior (bonus).

• Si un polinomio de alto orden parece ser necesario para la serie de tiempo, los modelos autorregresivos de media móvil integrada (ARIMA) pueden considerarse en cambio.

2.10. Forecasting

Forecasting

• En el tiempo \(T\), deseamos predecir la observación en la unidad de tiempo siguiente, \(T+1\), u otro valor en el futuro. Denotaremos el pronóstico \(\tau\) pasos hacia adelante (horizonte \(\tau\)) realizado en el tiempo \(T\) como \(\hat{y}_{T+\tau}(T)\).

2.10.1. Proceso constante

• La suavización exponencial de primer orden para el proceso constante está dada por

\[ \tilde{y}_{T}=\lambda y_{T}+(1-\lambda)\tilde{y}_{T-1} \]

• Se demostró también que \(f(t, \boldsymbol{\beta})=\beta_{0}\) puede ser estimado con \(\tilde{y}_{T}\). Dado que hasta el momento, el error aleatorio no puede ser predicho

\[ \hat{y}_{T+\tau}(T)=\tilde{y}_{T}=\hat{\beta}_{0}. \]

• Dado que pronósticos constantes pueden no ser correctos a medida que vamos acumulando observaciones, actualizamos nuestra predicción por medio de técnicas como rolling.

• Por ejemplo, si la observación en el tiempo \(T+1\) está disponible, nuestro pronóstico para futuras observaciones sería

(2.15)\[\begin{split} \begin{align*} \tilde{y}_{T+1} &= \lambda y_{T+1}+(1-\lambda)\tilde{y}_{T},\quad\text{o bien}\\ \tilde{y}_{T+1+\tau}(T+1) &= \lambda y_{T+1}+(1-\lambda)\tilde{y}_{T+\tau}(T)\\[4mm] \end{align*} \end{split}\]

• Para \(\tau=1\) la Ecuación (2.15) puede reescribirse como

  \[\begin{split} \begin{align*} \tilde{y}_{T+2}(T+1) &= \lambda y_{T+1}+(1-\lambda)\tilde{y}_{T+1}(T)\\ &= \tilde{y}_{T+1}(T)+\lambda(y_{T+1}-\tilde{y}_{T+1}(T))\\ &= \tilde{y}_{T+1}(T)+\lambda e_{T+1}(1), \end{align*} \end{split}\]

  donde \(e_{T+1}(1):=y_{T+1}-\tilde{y}_{T+1}(T)\) es llamado, predicción de un paso hacia adelante (one-step-ahead) o error de predicción.

Observación

• El pronóstico para la observación siguiente es, simplemente, el pronóstico actual, más una fracción del error cometido en el pronóstico de la observación actual

• Nótese que la velocidad de reacción del pronóstico al error de predicción depende del factor de descuento \(\lambda\)

2.11. Selección de \(\lambda\)

• Definimos la suma de cuadrados para los errores de predicción de horizonte 1 como

\[ SS_{E}(\lambda)=\sum_{t=1}^{T}e_{t}^{2}(1). \]

Observación

• Para un conjunto histórico de datos, podemos en general calcular \(SS_{E}(\lambda)\) para varios valores de \(\lambda\) y seleccionar aquel con la menor suma de errores de predicción al cuadrado.

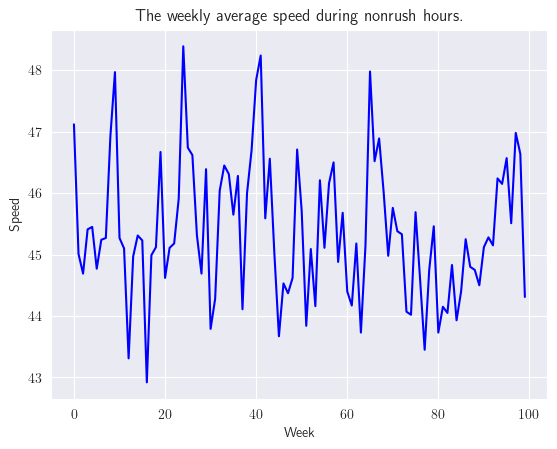
• Por ejemplo, supongamos que estamos interesados en la velocidad promedio en un tramo específico de una autopista durante las horas no pico. Durante el último año y medio (78 semanas), tenemos disponibles promedios semanales de la velocidad promedio en millas por hora entre las 10 a. m. y las 3 p. m. Los datos se presentan en la siguiente tabla

import pandas as pd

speed_df = pd.read_csv("https://raw.githubusercontent.com/lihkir/Data/main/weekly_average_speed.csv")
speed_df.head()

	week	speed
0	1	47.12
1	2	45.01
2	3	44.69
3	4	45.41
4	5	45.45

speed_ts = pd.Series(data=speed_df['speed'].values, index=speed_df.index)

speed_ts.head()

0    47.12
1    45.01
2    44.69
3    45.41
4    45.45
dtype: float64

• La siguiente figura muestra que los datos de la serie temporal siguen un proceso constante. Sin embargo, para suavizar la variación excesiva, podemos usar el suavizado exponencial de primer orden. La “mejor” constante de suavizado se puede determinar encontrando el valor de la constante de suavizado que minimiza la suma de los errores de predicción de un paso adelante al cuadrado.

plt.figure()
speed_ts.plot(color='b')
plt.title('The weekly average speed during nonrush hours.')
plt.xlabel('Week')
plt.ylabel('Speed');

import numpy as np
import matplotlib.pyplot as plt

lambda_vec = np.arange(0.1, 1.0, 0.1)

def sse_speed(sc):
    return measacc_fs(speed_ts, sc)['SSE'].values[0]

sse_vec = pd.Series()
for lambda_ in lambda_vec:
    sse_vec.loc[len(sse_vec)] = sse_speed(lambda_)

opt_lambda = sse_vec.min()

plt.plot(lambda_vec, sse_vec, marker='o', linestyle='-')
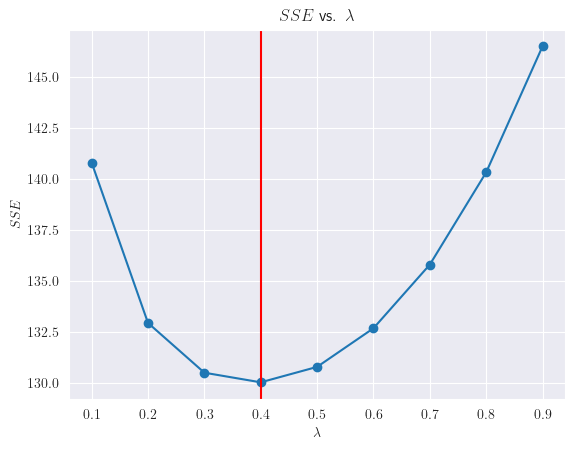
plt.title("$SSE$ vs. $\lambda$")
plt.xlabel('$\lambda$')
plt.ylabel('$SSE$')
plt.axvline(x=lambda_vec[sse_vec.idxmin()], color='red')
plt.show()

2.12. Intervalo de predicción

• El cálculo de intervalos de predicción requiere de la estimación de la varianza del error de predicción. Este tipo de técnicas serán estudiadas mas adelante en la presente sección

Proceso contante

• Para un proceso constante, el intervalo de predicción \(100(1-\alpha/2)\) para cualquier horizonte \(\tau\) está dado por

  \[ \tilde{y}\pm Z_{\alpha/2}\hat{\sigma}_{e}, \]

  donde \(\tilde{y}_{T}\) es la suavización exponencial de primer orden, \(Z_{\alpha/2}\) es el \(100(1-\alpha/2)\) percentíl de la distribución normal estándar, y \(\hat{\sigma}_{e}\) es la estimación de la desviación estándar de los errores predichos.

• Encontraremos solución a problemas de intervalo constante para todos los horizontes de predicción.

Proceso de tendencia lineal

• El pronóstico de horizonte \(\tau\) para el modelo de tendencia lineal está dado por

\[ \hat{y}_{T+\tau}=\hat{\beta}_{0, T}+\hat{\beta}_{1, T}(T+\tau)=\hat{\beta}_{0, T}+\hat{\beta}_{1, T}T+\hat{\beta}_{1, T}\tau=\hat{y}_{T}+\hat{\beta}_{1, T}\tau. \]

• En términos de suavizadores exponenciales

\[\begin{split} \begin{align*} \hat{y}_{T+\tau}(T) &= (2\tilde{y}_{T}^{(1)}-\tilde{y}_{T}^{(2)})+\tau\frac{\lambda}{1-\lambda}(\tilde{y}_{T}^{(1)}-\tilde{y}_{T}^{(2)})\\ &= \left(2+\frac{\lambda}{1-\lambda}\tau\right)\tilde{y}_{T}^{(1)}-\left(1+\frac{\lambda}{1-\lambda}\tau\right)\tilde{y}_{T}^{(2)}. \end{align*} \end{split}\]

• Nótese que las predicciones dependerán ahora del horizonte de predicción \(\tau\). En este caso, el \(100(1-\alpha/2)\) intervalo de predicción para cualquier horizonte de tiempo \(\tau\) está dado por (bonus)

  \[ \left(2+\frac{\lambda}{1-\lambda}\tau\right)\tilde{y}_{T}^{(1)}-\left(1+\frac{\lambda}{1-\lambda}\tau\right)\tilde{y}_{T}^{(2)}\pm Z_{\alpha/2}\frac{c_{\tau}}{c_{1}}\hat{\sigma}_{e}. \]

  donde

  \[ c_{i}^{2}=1+\frac{\lambda}{(2-\lambda)^{3}}[(10-14\lambda+5\lambda^{2})+2i\lambda(4-3\lambda)+2i^{2}\lambda^{2}]. \]

• A manera de ejemplo, consideremos los datos asociados al US Consumer Price Index (CPI). Como primera opción, realizaremos pronósticos para todo el año 2004 (pronósticos de 1 a 12 pasos por delante)

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

cpi_data = pd.read_csv("https://raw.githubusercontent.com/lihkir/Data/main/CPI.csv", skiprows=1, skipfooter=1, engine='python')

cpi_data.head()

	Year	Period	Consumer Price Index	Over-the-Year Percent Change	Over-the-Month Percent Change
0	2024	March	312.3	3.5%	0.6%
1	2024	February	310.3	3.2%	0.6%
2	2024	January	308.4	3.1%	0.5%
3	2023	December	306.7	3.4%	-0.1%
4	2023	November	307.1	3.1%	-0.2%

cpi_data['Date'] = cpi_data['Period'].astype(str) + '-' + cpi_data['Year'].astype(str)

cpi_data.index = cpi_data['Date']
cpi_data.drop('Date', axis=1, inplace=True)
cpi_data.head()

	Year	Period	Consumer Price Index	Over-the-Year Percent Change	Over-the-Month Percent Change
Date
March-2024	2024	March	312.3	3.5%	0.6%
February-2024	2024	February	310.3	3.2%	0.6%
January-2024	2024	January	308.4	3.1%	0.5%
December-2023	2023	December	306.7	3.4%	-0.1%
November-2023	2023	November	307.1	3.1%	-0.2%

cpi_ts = pd.Series(data=cpi_data['Consumer Price Index'].values, index=cpi_data.index)[::-1]

cpi_ts

Date
January-1913       9.8
February-1913      9.8
March-1913         9.8
April-1913         9.8
May-1913           9.7
                 ...  
November-2023    307.1
December-2023    306.7
January-2024     308.4
February-2024    310.3
March-2024       312.3
Length: 1335, dtype: float64

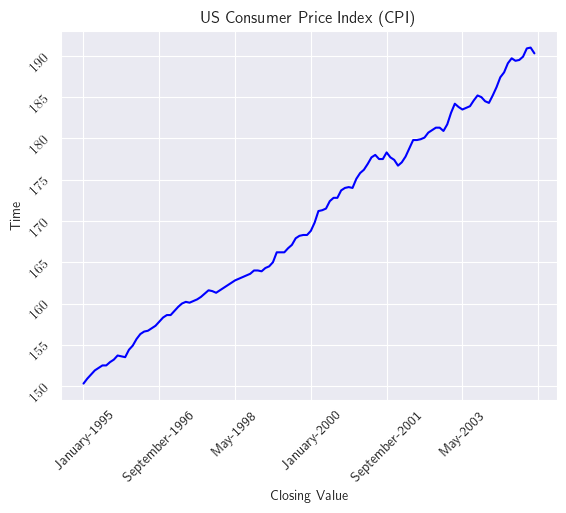
• Consideremos el US Consumer Price Index (CPI) de Estados Unidos desde enero de 1995 hasta diciembre de 2004. La siguiente figura muestra claramente que los datos exhiben una tendencia lineal.

cpi_dates = cpi_ts[cpi_ts.index.get_loc('January-1995'):cpi_ts.index.get_loc('December-2004')+1]

cpi_dates

Date
January-1995      150.3
February-1995     150.9
March-1995        151.4
April-1995        151.9
May-1995          152.2
                  ...  
August-2004       189.5
September-2004    189.9
October-2004      190.9
November-2004     191.0
December-2004     190.3
Length: 120, dtype: float64

fig, ax = plt.subplots()

cpi_dates.plot(ax=ax, color='b')
ax.set_title('US Consumer Price Index (CPI)')
ax.set_xlabel('Closing Value')
ax.set_ylabel('Time')
ax.tick_params(axis='x', rotation=45)
ax.tick_params(axis='y', rotation=45)

plt.show()

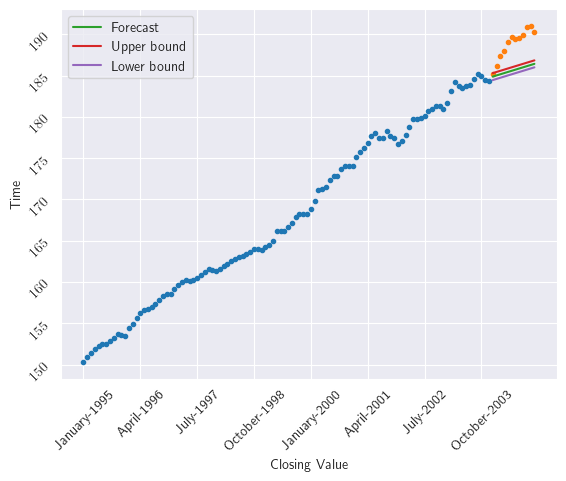
• En diciembre de 2003, realiza las previsiones para todo el año 2004 (previsiones de 1 a 12 pasos adelante)

lambda_ = 0.3
tau_length = 12

cpi_smooth1 = firstsmooth(cpi_dates.iloc[:-tau_length], lambda_)
cpi_smooth2 = firstsmooth(cpi_smooth1, lambda_)

cpi_hat = 2 * cpi_smooth1 - cpi_smooth2

tau = np.arange(1, tau_length+1)

T = len(cpi_smooth1)

cpi_forecast = (2 + tau * (lambda_ / (1 - lambda_))) * cpi_smooth1[T-1] - (1 + tau * (lambda_ / (1 - lambda_))) * cpi_smooth2[T-1]

ctau = np.sqrt(1 + (lambda_ / ((2 - lambda_)**3)) * (10 - 14 * lambda_ + 5 * (lambda_**2) + 2 * tau * lambda_ * (4 - 3 * lambda_) + 2 * (tau**2) * (lambda_**2)))

alpha_lev = 0.05

sig_est = np.sqrt(np.var(cpi_dates.iloc[1:] - cpi_hat[:-1]))

cl = np.quantile(ctau / ctau[0] * sig_est, 1 - alpha_lev / 2)

fig, ax = plt.subplots()
ax.plot(cpi_dates.index[:-tau_length], cpi_dates.iloc[:-tau_length].values, marker='o', linestyle='', markersize=3)
ax.plot(cpi_dates.index[-tau_length:], cpi_dates.iloc[-tau_length:].values, marker='o', linestyle='', markersize=3)
ax.plot(cpi_dates.index[-tau_length:], cpi_forecast, label='Forecast')
ax.plot(cpi_dates.index[-tau_length:], cpi_forecast + cl, label='Upper bound')
ax.plot(cpi_dates.index[-tau_length:], cpi_forecast - cl, label='Lower bound')
n = 15
plt.xticks(range(0, len(cpi_dates.index), n), rotation=45)
ax.set_xlabel('Closing Value')
ax.set_ylabel('Time')
ax.tick_params(axis='x', rotation=45)
ax.tick_params(axis='y', rotation=45)
plt.legend()
plt.show()

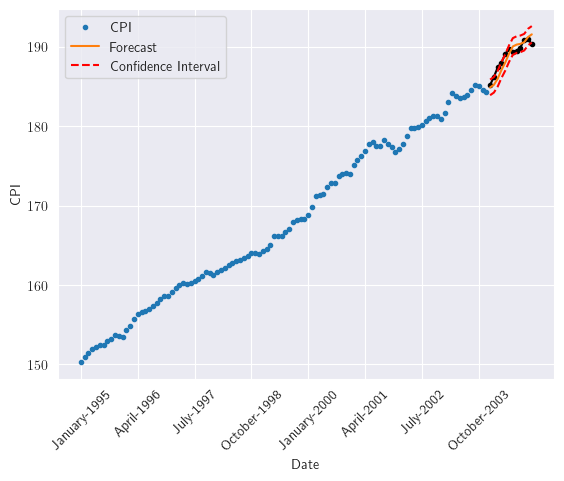
• Como segunda opción. En diciembre de 2003, hacer el pronóstico para enero de 2004. Luego, cuando los datos de enero de 2004 estén disponibles, hacer el pronóstico para febrero de 2004 (solo pronósticos de un paso por delante)”

import numpy as np
from scipy.stats import norm

lambda_ = 0.3
T = 108
tau = 12
alpha_lev = 0.05
cpi_forecast = np.zeros(tau)
cl = np.zeros(tau)
cpi_smooth1 = np.zeros(T + tau)
cpi_smooth2 = np.zeros(T + tau)

for i in range(1, tau + 1):
    cpi_smooth1[:T + i - 1] = firstsmooth(y=cpi_dates.iloc[:T + i - 1], lambda_=lambda_)
    cpi_smooth2[:T + i - 1] = firstsmooth(y=cpi_smooth1[:T + i - 1], lambda_=lambda_)
    cpi_forecast[i - 1] = (2 + (lambda_ / (1 - lambda_))) * cpi_smooth1[T + i - 2] - \
                          (1 + (lambda_ / (1 - lambda_))) * cpi_smooth2[T + i - 2] # horizon one each time
    cpi_hat = 2 * cpi_smooth1[:T + i - 1] - cpi_smooth2[:T + i - 1]
    sig_est = np.sqrt(np.var(cpi_dates.iloc[1:T + i - 1] - cpi_hat[:-1]))
    cl[i - 1] = norm.ppf(1 - alpha_lev / 2) * sig_est

plt.figure()
plt.plot(cpi_dates.index[:-tau], cpi_dates.iloc[:-tau].values, marker='o', linestyle='', markersize=3, label='CPI')
plt.plot(cpi_dates.index[-tau:], cpi_dates.iloc[-tau:].values, marker='o', markersize=3, color='black')
plt.plot(cpi_dates.index[-tau:], cpi_forecast, label='Forecast')
plt.plot(cpi_dates.index[-tau:], cpi_forecast + cl, linestyle='--', color='red', label='Confidence Interval')
plt.plot(cpi_dates.index[-tau:], cpi_forecast - cl, linestyle='--', color='red')
plt.legend()
n = 15
plt.xticks(range(0, len(cpi_dates.index), n), rotation=45)
plt.xlabel('Date')
plt.ylabel('CPI')
plt.show()

2.13. Estimación de \(\sigma_{e}^{2}\)

• En el proceso de estimar la varianza de los errores de pronóstico, representada como \(\sigma_{e}^{2}\), frecuentemente se postula que el modelo subyacente (por ejemplo, constante, tendencia lineal) es correcto e invariante en el tiempo (predicciones precisas y estables a medida que se avanza en el tiempo). Bajo estas condiciones, dos metodologías distintas están disponibles para estimar \(\sigma_{e}^{2}\)

Bonus

• Encuentre la estimación de la varianza de los errores de pronóstico \(\sigma_{e}^{2}\) para el modelo de suavización exponencial. Utilice los siguientes documentos como guía Peter Wanke et. al y Kuliah Genap, así como aquellos que encuentre en su revisión.

1. Dado el pronóstico one-step-ahead definido como \(e_{T}(1)=y_{T}-\hat{y}_{T}(T-1)\). El objetivo es aplicar el modelo a los datos históricos y obtener la varianza del error de pronóstico a calcular

\[ \sigma_{e}^{2}=\frac{1}{T}\sum_{t=1}^{T}e_{t}^{2}(1)=\frac{1}{T}\sum_{t=1}^{T}(y_{t}-\hat{y}_{t}(t-1))^{2}. \]

• Nótese que en el cálculo de la varianza, la media del ajuste no fue necesaria, ya que para el modelo correcto los pronósticos son insesgados; esto es, el valor esperado de los errores de pronóstico es 0.

• A medida que se recopilan más datos, la varianza de los errores de pronóstico puede ser actualizada

\[ \hat{\sigma}_{eT+1}=\frac{1}{T+1}\left(T\hat{\sigma}_{e, T}^{2}+e_{T+1}^{2}(1)\right). \]

• Puede resultar contraintuitivo tener una varianza constante de errores de pronóstico para todos los horizontes de predicción. En su lugar, podemos definir \(\sigma_{e}^{2}(\tau)\) como la varianza del error de pronóstico a \(\tau\) pasos hacia adelante y estimarla mediante

(2.16)\[ \hat{\sigma}_{e}^{2}(\tau)=\frac{1}{T-\tau+1}\sum_{t=\tau}^{T}e_{1}^{2}(\tau). \]

• Por lo tanto, la estimación en la Ecuación (2.16) puede ser utilizada en los cálculos del intervalo de predicción para el pronóstico a \(\tau\) pasos hacia adelante.

2. Para el segundo método de estimación de \(\sigma_{e}^{2}\), primero definiremos la desviación media absoluta \(\Delta\) como

   \[ \Delta = \text{E}(|e-\text{E}(e)|) \]

   y, asumiendo que el modelo es correcto, calcular su estimación mediante

   (2.17)\[ \hat{\Delta}_{T}=\delta|e_{T}(1)|+(1-\delta)\hat{\Delta}_{T-1}. \]

   Entonces, el estimador de \(\sigma_{e}^{2}\) está dado por [Montgomery et al., 1990] (bonus)

   \[ \hat{\sigma}_{e, T}=1.25\hat{\Delta}_{T}. \]

2.14. Adaptación actualizada del factor de descuento

• Cambios en el modelo subyacente de series temporales dificultarán que el suavizador exponencial con factor de descuento fijo siga estos cambios. Por lo tanto, surge la necesidad de monitorear y, si es necesario, modificar el factor de descuento. Al hacerlo, el factor de descuento se adaptará a los cambios en el modelo de series temporales.

• Para ello, emplearemos el procedimiento descrito originalmente por [Trigg and Leach, 1967] para un único factor de descuento. Como ejemplo, consideraremos el suavizador exponencial de primer orden y lo modificaremos de la siguiente manera:

(2.18)\[ \hat{y}_{T}=\lambda_{T}y_{T}+(1-\lambda_{T})\hat{y}_{T-1}. \]

• Nótese que en la Ecuación (2.18), el factor de descuento \(\lambda_{T}\) se introduce como una función del tiempo y, por lo tanto, se le permite adaptarse a los cambios en el modelo de series temporales.

• También definimos el error de suavizado como

  \[ Q_{T}=\delta e_{T}(1)+(1-\delta)Q_{T-1}, \]

  donde \(\delta\) es un parámetro de suavización.

• Por último, definimos la señal de seguimiento como

  \[ \frac{Q_{T}}{\hat{\Delta}_{T}}, \]

  donde \(\hat{\Delta}_{T}\) está dado por la Ecuación (2.17).

• Se espera que este cociente sea cercano a 0 cuando el sistema de predicción funciona bien, y que se acerque a \(\pm1\) cuando empiece a fallar. De hecho, [Trigg and Leach, 1967] sugieren fijar el factor de descuento en

  (2.19)\[ \lambda_{T}=\left|\frac{Q_{T}}{\hat{\Delta}_{T}}\right|, \]

  Donde \(\hat{\Delta}_{T}\) está dado por la Ecuación (2.17). La Ecuación (2.19) permitirá actualizar automáticamente el factor de descuento.

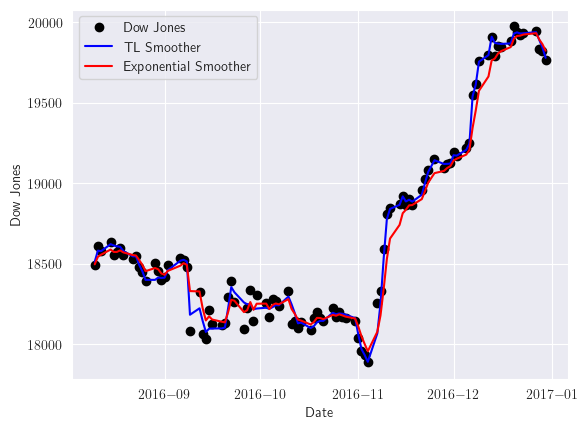
• La siguiente figura muestra dos suavizadores exponenciales simples para el Índice Dow Jones, uno con \(\lambda\) fijo de 0.3 y otro con actualización adaptativa basada en el método Trigg-Leach dado en la Ecuación (2.19). Visualizaremos los últimos cien registros para poder apreciar mejor las predicciones de cada modelo

def tlsmooth(y, delta_, y_tilde_start=None, lambda_start=1):
    T = len(y)
    
    Qt = np.zeros(T)
    Dt = np.zeros(T)
    y_tilde = np.zeros(T)
    lambd = np.zeros(T)
    err = np.zeros(T)
    
    lambd[0] = lambda_start
    if y_tilde_start is None:
        y_tilde[0] = y[0]
    else:
        y_tilde[0] = y_tilde_start
    
    for i in range(1, T):
        err[i] = y[i] - y_tilde[i-1]
        Qt[i] = delta_ * err[i] + (1 - delta_) * Qt[i-1]
        Dt[i] = delta_ * abs(err[i]) + (1 - delta_) * Dt[i-1]
        lambd[i] = abs(Qt[i] / Dt[i])
        y_tilde[i] = lambd[i] * y[i] + (1 - lambd[i]) * y_tilde[i-1]
    
    return np.column_stack((y_tilde, lambd, err, Qt, Dt))

out_tl_dji = tlsmooth(djia_ts, 0.3)

last_fc = 100

plt.plot(djia_ts.index[-last_fc:], djia_ts[-last_fc:], marker='o', linestyle='', color='black', label='Dow Jones')
plt.plot(djia_ts.index[-last_fc:], out_tl_dji[-last_fc:, 0], color='blue', label='TL Smoother')
plt.plot(djia_ts.index[-last_fc:], dji_smooth1[-last_fc:], color='red', label='Exponential Smoother')
plt.xlabel('Date')
plt.ylabel('Dow Jones')
plt.legend()
plt.show()

2.15. Evaluación del modelo

• Si el modelo de pronóstico funciona como se esperaba, los errores de pronóstico deberían no exhibir ningún patrón o estructura; es decir, no deberían estar correlacionados. Por lo tanto, siempre es una buena idea verificar esto. Puede hacerlo calculando el ACF muestral de los errores de pronóstico de

\[ r_{k}=\frac{\displaystyle{\sum_{t=k}^{T-1}[e_{t}(1)-\overline{e}][e_{t-k}(1)-\overline{e}]}}{\displaystyle{\sum_{T=0}^{T-1}[e_{t}(1)-\overline{e}]^{2}}},~\text{donde}~\overline{e}=\frac{1}{n}\sum_{t=1}^{T}e_{t}(1). \]

Observación

• Si los errores de pronóstico de un paso adelante en realidad no están correlacionados, las autocorrelaciones muestrales para cualquier rezago \(k\) deben estar alrededor de 0 con un error estándar \(1/\sqrt{T}\).

• De ahí una autocorrelación muestral para cualquier rezago \(k\) que se encuentre fuera de los límites \(\pm2/\sqrt{T}\) requerirán una mayor investigación del modelo.

2.16. Suavización exponencial para datos estacionales

• Algunos datos de series de tiempo exhiben patrones cíclicos o estacionales que no se pueden modelar efectivamente utilizando el modelo polinómico de la Ecuación (2.14). Hay varios enfoques disponibles para el análisis de dichos datos.

• La metodología en la que nos centraremos fue introducida originalmente por [Holt, 2004] y [Winters, 1960] y generalmente se conoce como método de Winters, donde se realiza un ajuste estacional al modelo de tendencia lineal.

2.16.1. Modelo estacional aditivo

• Para el caso del modelo estacional aditivo, asumiremos que la serie temporal estacional se puede representar mediante el siguiente modelo:

  (2.20)\[ y_{t}=L_{t}+S_{t}+\varepsilon_{t}, \]

  donde \(L_{t}\) representa el nivel o componente de tendencia lineal y puede a su vez ser representado por \(\beta_{0}+\beta_{1}t\); \(S_{t}\) representa el ajuste estacional con \(S_{t}=S_{t+s}=S_{t+2s}=\cdots\) para \(t=1, 2,\cdots, s-1\) donde \(s\) es la longitud de período (estación) de los ciclos; y suponemos que \(\varepsilon_{t}\) es no correlacionado con media 0 y varianza constante \(\sigma_{\varepsilon}^{2}\).

• Una restricción habitual de este modelo es que los ajustes estacionales suman cero durante un periodo (evitar tendencia acumulativa en los ajustes estacionales),

\[ \sum_{t=1}^{s}S_{t}=0. \]

• En el modelo dado en la Ecuación (2.20), para pronosticar las observaciones futuras, emplearemos suavizadores exponenciales de primer orden con diferentes factores de descuento.

• El procedimiento para actualizar las estimaciones de los parámetros una vez que se obtiene la observación actual \(y_{T}\) es el siguiente.

1. Actualizar la estimación de \(L_{t}\) usando

   (2.21)\[ \hat{L}_{t}=\lambda_{1}(y_{T}-\hat{S}_{T-s})+(1-\lambda_{1})(\hat{L}_{T-1}+\hat{\beta}_{1, T-1}), \]

   donde \(0<\lambda_{1}<1\). Cabe señalar que en la Ecuación (2.21), la primera parte puede verse como el valor “actual” de \(L_{T}\) y la segunda parte como el pronóstico de \(L_{T}\) basado en las estimaciones en \(T-1\).

2. Actualizar la estimación de \(\beta_{1}\) usando

   (2.22)\[ \hat{\beta}_{1, T}=\lambda_{2}(\hat{L}_{T}-\hat{L}_{T-1})+(1-\lambda_{2})\hat{\beta}_{1, T-1}, \]

   donde \(0<\lambda_{2}<1\). Como en el Paso 1, la estimación de \(\beta_{1}\) en la Ecuación (2.22) puede verse como la combinación lineal del actual valor de \(\beta_{1}\) y su pronóstico an el tiempo \(T-1\).

3. Actualizar la estimación de \(S_{t}\) usando

   (2.23)\[ \hat{S}_{T}=\lambda_{3}(y_{T}-\hat{L}_{T})+(1-\lambda_{3})\hat{S}_{T-s}, \]

   donde \(0<\lambda_{3}<1\).

4. Finalmente, el pronóstico \(\tau\) pasos hacia adelante, \(\hat{y}_{T+\tau}(T)\), es

   \[ \hat{y}_{T+\tau}(T)=\hat{L}_{T}+\hat{\beta}_{1, T}\tau+\hat{S}_{T}(\tau-s). \]

• Estimar los valores iniciales de una suavización exponencial es crucial. Para un conjunto dado de datos históricos con \(n\) estaciones (\(ns\) observaciones), podemos usar las estimaciones de mínimos cuadrados del siguiente modelo:

  (2.24)\[ y_{t}=\beta_{0}+\beta_{1}t+\sum_{i=1}^{s-1}\gamma_{i}(I_{t, i}-I_{t, s})+\varepsilon_{t}, \]

  donde

  \[\begin{split} I_{t, i}= \begin{cases} 1, & t=i, i+s, i+2s, \dots\\ 0, & \text{en otro caso}. \end{cases} \end{split}\]

• Las estimaciones de mínimos cuadrados de los parámetros de la Ecuación (2.24) se utilizan para obtener los valores iniciales como

\[\begin{split} \begin{align*} \hat{\beta}_{0, 0} &= \hat{L}_{0}=\hat{\beta}_{0}\\ \hat{\beta}_{1, 0} &= \hat{\beta}_{1}\\ \hat{S}_{j-s} &= \hat{Y}_{j},~\text{para}~ 1\leq j\leq s-1\\ \hat{S}_{0} &= -\sum_{j=1}^{s-1}\hat{y}_{j}. \end{align*} \end{split}\]

• Estos son valores iniciales de los parámetros del modelo en el origen original de tiempo, \(t = 0\). Para realizar pronósticos desde el origen correcto de tiempo, la componente permanente debe trasladarse al tiempo \(T\) calculando \(\hat{L}_{T}=\hat{L}_{0}+ns\hat{\beta}_{1}\). Alternativamente, se podrían suavizar los parámetros usando las Ecuaciones (2.21)-(2.23) para periodos de tiempo \(t = 1, 2,\dots, T\) [Hyndman et al., 2008].

Observación

• Intervalos de predicción como en el caso del suavizado no estacional, requerirían estimación de la varianza del error de predicción. El enfoque más común es utilizar la relación entre las técnicas de suavizado exponencial y modelos ARIMA que abordaremos en el siguiente capítulo, y estimar la variación del error de predicción acordemente.

2.16.2. Modelo estacional multiplicativo

• Si la amplitud del patrón estacional es proporcional al nivel medio de la serie temporal estacional, el siguiente modelo estacional multiplicativo será el más adecuado

  (2.25)\[ y_{t}=L_{t}S_{t}+\varepsilon_{t}, \]

  donde \(L_{t}\) una vez más representa la componente permanente (i.e. \(\beta_{0}+\beta_{1}t\)); \(S_{t}\) representa el ajuste estacional con \(S_{t}=S_{t+s}=S_{t+2s}=\cdots\) para \(t=1,2,\dots, s-1\), donde \(s\) es la longitud del periodo de los ciclos; y \(\varepsilon_{t}\) se supone no correlacionado con media 0 y varianza constante \(\sigma_{\varepsilon}^{2}\).

• La restricción para los ajustes estacionales en este caso se convierte en

  \[ \sum_{t}^{s}S_{t}=s. \]

• Como en el modelo aditivo, emplearemos tres suavizadores exponenciales para estimar los parámetros en la Ecuación (2.25)

1. Actualizar el estimador de \(L_{T}\) usando

   \[ \hat{L}_{T}=\lambda_{1}\frac{y_{T}}{\hat{S}_{T-s}}+(1-\lambda_{1})(\hat{L}_{T-1}+\hat{\beta}_{1, T-1}), \]

   donde \(0<\lambda_{1}<1\).

2. Actualizar el estimador de \(\beta_{1}\) utilizando

   \[ \hat{\beta}_{1, T}=\lambda_{2}(\hat{L}_{T}-\hat{L}_{T-1})+(1-\lambda_{2})\hat{\beta}_{1, T-1}, \]

   donde \(0<\lambda<1\).

3. Actualizar la estimación de \(S_{t}\) usando

   \[ \hat{S}_{T}=\lambda_{3}\frac{y_{T}}{\hat{L}_{T}}+(1-\lambda_{3})\hat{S}_{T-s}, \]

   donde \(0<\lambda_{3}<1\).

4. El pronóstico \(\tau\) pasos hacia adelante, \(\hat{y}_{T+\tau}(T)\), es

   \[ \hat{y}_{T+\tau}(T)=(\hat{L}_{T}+\hat{\beta}_{1, T}\tau)\hat{S}_{T}(\tau-s). \]

• Supongamos que un registro que consta de \(n\) estaciones de datos es disponible. De este conjunto de datos históricos, los valores iniciales, \(\hat{\beta}_{0, 0}, \hat{\beta}_{1, 0}\) y \(\hat{S}_{0}\), se puede calcular como

  \[ \hat{\beta}_{0, 0}=\hat{L}_{0}=\frac{\overline{y}_{n}-\overline{y}_{1}}{(n-1)s}, \]

  donde

  \[ \overline{y}_{i}=\frac{1}{s}\sum_{t=(i-1)s+1}^{is}y_{t} \]

  y

  \[\begin{split} \begin{align*} \hat{\beta}_{1, 0} &= \overline{y}_{1}-\frac{s}{2}\hat{\beta}_{0, 0}\\ \hat{S}_{j-s} &= s\frac{\hat{S}_{j}^{\star}}{\sum_{i=1}^{s}\hat{S}_{i}^{\star}}~\text{para}~1\leq j\leq s, \end{align*} \end{split}\]

  donde

  \[ \hat{S}_{j}^{\star}=\frac{1}{n}\sum_{t=1}^{n}\frac{y_{(t-1)s+j}}{\overline{y}_{t}-((s+1)/2-j)\hat{\beta}_{0}}. \]

  Para más detalles ver [Montgomery et al., 1990] y [Abraham and Ledolter, 2009].

2.17. Librería statsmodels.tsa.holtwinters

import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns
import statsmodels.api as sm
from sklearn.metrics import mean_absolute_error
import itertools
import warnings
from statsmodels.tools.sm_exceptions import ConvergenceWarning
warnings.simplefilter('ignore', ConvergenceWarning)
from statsmodels.tsa.holtwinters import ExponentialSmoothing
from statsmodels.tsa.holtwinters import SimpleExpSmoothing
from statsmodels.tsa.seasonal import seasonal_decompose
import statsmodels.tsa.api as smt

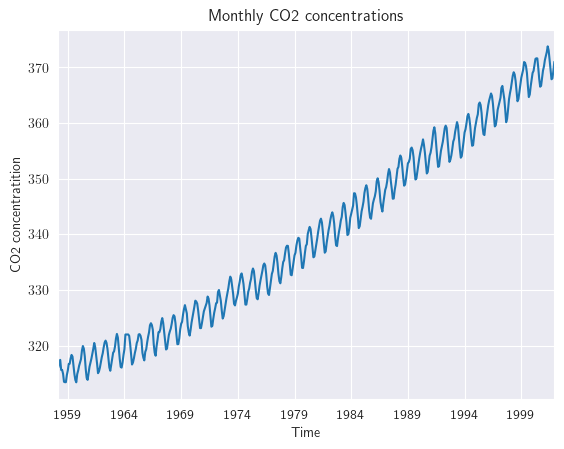
• Consideremos, nuevamente, el objetivo de estimar la cantidad de *contaminación atmosférica por dióxido de carbono a partir de muestras continuas de aire en el Observatorio Mauna Loa, Hawai, EE. UU. Período de registro: marzo de 1958 - diciembre de 2001.

data = sm.datasets.co2.load_pandas()
y = data.data
y.head()

	co2
1958-03-29	316.1
1958-04-05	317.3
1958-04-12	317.6
1958-04-19	317.5
1958-04-26	316.4

y = y['co2'].resample('MS').mean()
y.head()

1958-03-01    316.100000
1958-04-01    317.200000
1958-05-01    317.433333
1958-06-01           NaN
1958-07-01    315.625000
Freq: MS, Name: co2, dtype: float64

y.isnull().sum()

5

y = y.fillna(y.bfill())
y.isnull().sum()

0

y.plot()
plt.title('Monthly CO2 concentrations')
plt.xlabel('Time')
plt.ylabel('CO2 concentratition');
plt.show()

• Dividimos en esta ocasión nuestro dataset en conjunto de entrenamiento y de prueba. En este caso el conjunto de prueba corresponde a los últimos 48 meses

tau_test = 48
train = y[:-tau_test]
test  = y[-tau_test:]
print((len(train), len(test)))

(478, 48)

• La siguiente función nos permitirá graficar los conjuntos de entrenamiento, prueba y las respectivas predicciones del conjunto de prueba. Además, mostraremos en el título de estas figuras la métrica MAE

def plot_model(train, test, y_pred, title):
    
    mae = mean_absolute_error(test, y_pred)
    train[-112:].plot(legend=True, label="Train", title=f"{title}, MAE: {round(mae, 2)}")
    test.plot(legend=True, label="Test")
    y_pred.plot(legend=True, label="Prediction")
    plt.show()

2.17.1. Simple Exponential Smoothing

• Cada una de las funciones optimizadoras permitirán encontrar el mejor parámetro \(\alpha\) para obtener aquel modelo que minimiza en este caso la métrica MAE

def ses_optimizer(train, alphas, step):

    best_alpha, best_mae = None, float("inf")

    for alpha in alphas:
        ses_model = SimpleExpSmoothing(train).fit(smoothing_level=alpha, optimized=False)
        y_pred = ses_model.forecast(step)
        mae = mean_absolute_error(test, y_pred)

        if mae < best_mae:
            best_alpha, best_mae = alpha, mae

    return best_alpha, best_mae

def ses_model_tuning(train , test, step, title="Model Tuning - Single Exponential Smoothing"):
    
    alphas = np.arange(0.8, 1, 0.01)
    best_alpha, best_mae = ses_optimizer(train, alphas, step=step)
    final_model = SimpleExpSmoothing(train).fit(smoothing_level=best_alpha, optimized=False)
    y_pred = final_model.forecast(step)
    mae = mean_absolute_error(test, y_pred)
    
    plot_model(train, test, y_pred, title)

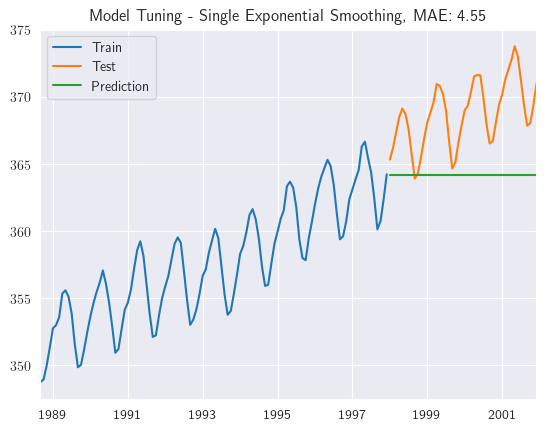
• Observemos las predicciones obtenidas por medio del modelo de suavización exponencial simple

ses_model_tuning(train, test, step=tau_test)

2.17.2. Double Exponential Smoothing

• ExponentialSmoothing(train, trend=trend): Crea una instancia de un modelo de suavización exponencial. Toma como argumento la serie temporal de entrenamiento train y especifica el tipo de tendencia (lineal o exponencial) mediante el parámetro trend.

• .fit(smoothing_level=alpha, smoothing_slope=beta): Ajusta el modelo a los datos de entrenamiento. Los parámetros smoothing_level y smoothing_slope controlan el nivel de suavizado de la serie temporal y de la tendencia, respectivamente. Estos parámetros se establecen en los valores dados por alpha y beta.

def des_optimizer(train, alphas, betas, trend, step):

    best_alpha, best_beta, best_mae = None, None, float("inf")

    for alpha in alphas:
        for beta in betas:
            des_model = ExponentialSmoothing(train, trend=trend).fit(smoothing_level=alpha, smoothing_slope=beta)
            y_pred = des_model.forecast(step)
            mae = mean_absolute_error(test, y_pred)
            if mae < best_mae:
                best_alpha, best_beta, best_mae = alpha, beta, mae

    return best_alpha, best_beta, best_mae

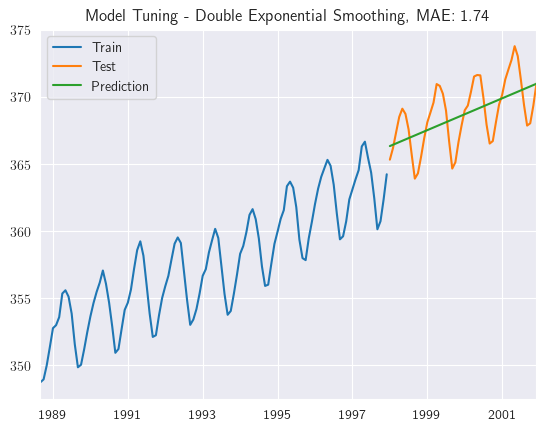
def des_model_tuning(train , test, step, trend, title="Model Tuning - Double Exponential Smoothing"):
    
    alphas = np.arange(0.01, 1, 0.10)
    betas = np.arange(0.01, 1, 0.10)
    best_alpha, best_beta, best_mae = des_optimizer(train, alphas, betas, trend=trend, step=step)
    final_model = ExponentialSmoothing(train, trend=trend).fit(smoothing_level=best_alpha, smoothing_slope=best_beta)
    y_pred = final_model.forecast(step)
    mae = mean_absolute_error(test, y_pred)
    
    plot_model(train, test, y_pred, title)

des_model_tuning(train, test, step=tau_test, trend='add')

2.17.3. Triple Exponential Smoothing

• En ExponentialSmoothing de la biblioteca statsmodels se especifican los componentes del modelo, como la tendencia y la estacionalidad, utilizando los argumentos trend y seasonal.

• Se especifica el número de periodos estacionales utilizando el argumento seasonal_periods. Los parámetros de suavizado (smoothing_level, smoothing_slope y smoothing_seasonal) se establecen en los valores proporcionados en la lista comb.

def tes_optimizer(train, abg, trend, seasonal,  seasonal_periods, step):
    
    best_alpha, best_beta, best_gamma, best_mae = None, None, None, float("inf")
    for comb in abg:
        tes_model = ExponentialSmoothing(train, trend=trend, seasonal=seasonal, seasonal_periods=seasonal_periods).\
            fit(smoothing_level=comb[0], smoothing_slope=comb[1], smoothing_seasonal=comb[2])
        y_pred = tes_model.forecast(step)
        mae = mean_absolute_error(test, y_pred)
        if mae < best_mae:
            best_alpha, best_beta, best_gamma, best_mae = comb[0], comb[1], comb[2], mae

    return best_alpha, best_beta, best_gamma, best_mae

def tes_model_tuning(train , test, step, trend, seasonal, seasonal_periods, title="Model Tuning - Triple Exponential Smoothing"):
    
    alphas = betas = gammas = np.arange(0.10, 1, 0.10)
    abg = list(itertools.product(alphas, betas, gammas))
    best_alpha, best_beta, best_gamma, best_mae = tes_optimizer(train, abg=abg, trend=trend, seasonal=seasonal, seasonal_periods=seasonal_periods, step=step)
    final_model = ExponentialSmoothing(train, trend=trend, seasonal=seasonal).fit(smoothing_level=best_alpha, smoothing_slope=best_beta, smoothing_seasonal=best_gamma)
    y_pred = final_model.forecast(step)
    mae = mean_absolute_error(test, y_pred)
    plot_model(train, test, y_pred, title)
    
    return best_alpha, best_beta, best_gamma, best_mae

best_alpha, best_beta, best_gamma, best_mae = tes_model_tuning(train, test, step=tau_test, trend='add', seasonal='add', seasonal_periods=12)

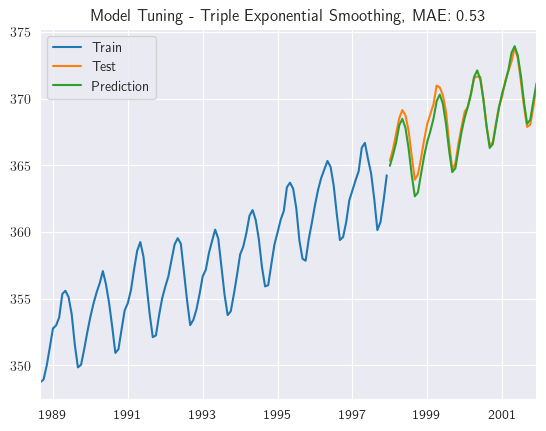
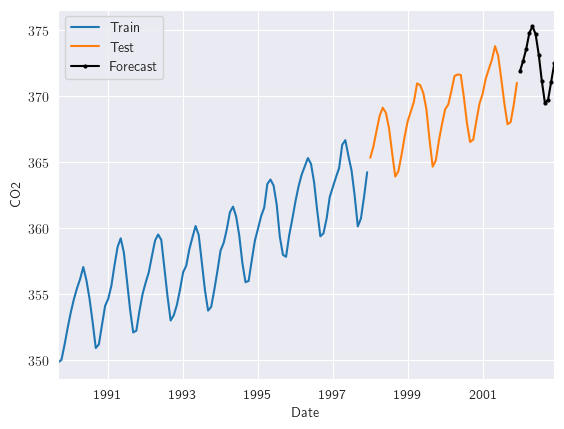
• Realizamos ahora predicciones para datos fuera de la muestra, en este caso pronosticamos un horizonte de 12 meses de CO2

def tes_final_model(y, best_alpha, best_beta, best_gamma, step, trend='add', seasonal='add'):
  final_model = ExponentialSmoothing(y, trend=trend, seasonal=seasonal).fit(smoothing_level=best_alpha, smoothing_slope=best_beta, smoothing_seasonal=best_gamma)
  feature_predict = final_model.forecast(step)
  return feature_predict

y_pred = tes_final_model(y, best_alpha, best_beta, best_gamma, step=12)

train[-100:].plot(label = 'Train');
test.plot(label = 'Test');
y_pred.plot(label = 'Forecast', color = 'black', marker='o', markersize=2);
plt.xlabel('Date')
plt.ylabel('CO2')
plt.legend();

Resumen

• Este capítulo trata de los enfoques de suavización exponencial para datos de series temporales. Los enfoques pueden ampliarse fácilmente para la predicción mediante la inclusión de términos como el factor de suavización, factor de tendencia y factor de estacionalidad.

• El suavizado exponencial de orden único realiza la suavización utilizando solo el factor \(\lambda\), que se amplía con los factores \(\alpha,\,\beta\) de segundo orden al incluir tendencia. La suavización de tercer orden incorpora todos los factores, tendencia y estacionalidad en el modelo.

• En este capítulo se han tratado todos estos modelos en detalle con su implementación en Python. El enfoque de suavizado exponencial puede utilizarse para pronosticar series temporales estacionarias. Sin embargo, esta suposición puede no ser cierta. Se recomienda el suavizado exponencial de orden superior para estos casos, pero su cálculo es difícil y costoso computacionalmente. Por lo tanto, para hacer frente a este planteamiento, se utilizan otras técnicas de previsión como el modelo ARIMA, que se tratará en la siguiente sección.